基于离散变换域的语音合成算法研究

李亚文

（商洛学院 物理与电子信息工程系，陕西商洛 726000）

语音合成技术的发展起步较早，早在1791年由Wolfgang Von Kempelen等[1]发明的语音合成器，使得机器能用法语拼出完整的短语，英语文语转换系统发展比较早，代表性是DECTalk语音合成器[2]，它可以发出7种不同音色的语音信号，用户可以任意选择，德国Franunhofer学会开发了DECTalk德语版本，它还被不同的国家转化为乌克兰语、俄语、匈牙利语等。从20世纪80年代我国自动化研究所、声学研究所、社科院，就开始了语音合成方面的研究[3]，目前汉语语音合成系统都是采用波形拼接合成技术[4]，基于参数的语音合成算法，基于数据单元挑选语音合成算法和基于数据驱动的语音合成方法，以及语音识别中的数据驱动建模、最优搜索等[1-2,4]优秀的算法思想在语音合成中得到了广泛的应用，然而这些算法各有优缺点，主要问题是占用的数据存储空间较大，可懂度不高，从而影响了发音的质量，合成的语音音色单一，韵律结构预测误差较大等。本文继承基于参数的语音合成算法中线性预测的思想，提出了一种基于离散变换域的语音信号合成方法，对采样的语音信号进行滤波，送入预测器中并进行语音预测，采用线性预测的方法压缩语音数据量，大大的降低了语音信号的带宽，再对语音信号加窗、基音提取，最后在声道模型中重构合成语音信号。

1 离散变换域

离散信号相比模拟信号在传输中有明显的优势，因此大部分的信号传输都是要将模拟信号转换为数字信号，其中语音信号的传输也是一样。将时域的离散系统转化为变换域（Z域）中，在变化域中的分析研究语音信号的重构合成。

N阶线性时不变（LTI）的离散系统的数学模型是常系数N阶线性差分方程[5]，它的一般形式为：

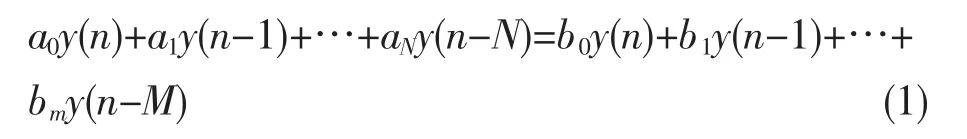
分析离散系统响应的结果就是求解式(1)N阶差分方程[5]的过程，其中差分方程中的系数aN,bm由系统的元件参数决定。

时域分析中，由系统的单位脉冲响应h(n)，可判断离散时间系统的因果稳定性。由于输出变化发生在输入变化之后，因此y(n)只取决于此时及以前的激励x(n)、x(n+1)、离散LTI系统具有因果性的充分必要条件为：h(n)=0,n＜0，离散LTI系统稳定的充分必要条件为单位脉冲响应满足绝对可和，即

为了分析离散系统响应和系统特性，引入了离散系统Z变换，方便了计算，可将时域的数学模型差分方程转化为线性的代数方程；通过分析单位冲激响应h(n)对应的Z变换H(z)的零极点分布间接分析系统的因果稳定性。

N阶LTI离散系统的差分方程一般形式为：

对系统两边同时取Z变换得到：

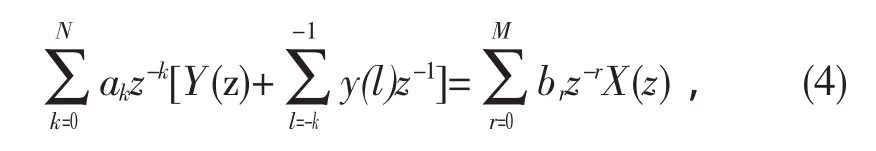
其中式(4)中,y(l)是初始条件。 这样离散系统的

时域响应可表示为：

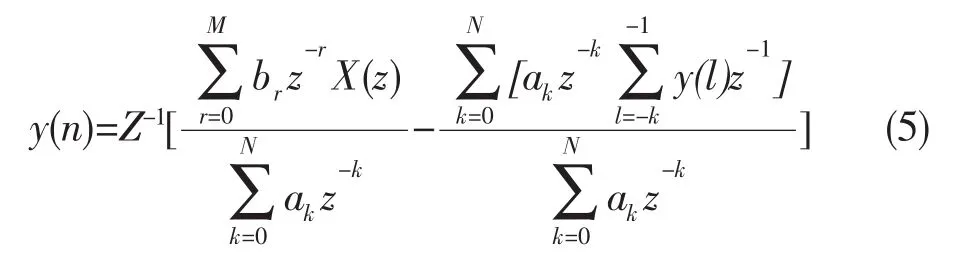
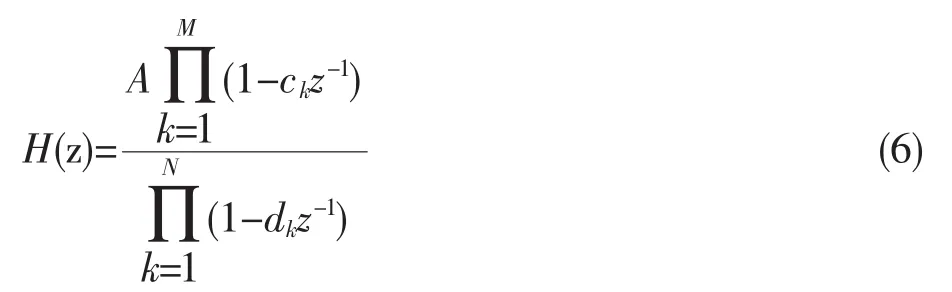
式(6)中,{ck}是 H(z)的零点；{dk}是 H(z)的极点。由式（6）中H(z)的表示式中除了系数A外，H(z)可由其零、极点确定。

H(z)与h(n)是一对Z变换对,所以只要知道H(z)在z平面上的零、极点分布情况，就可以知道系统的脉冲响应h(n)变化规律[5]，进而可以判断系统的因果稳定性。

2 语音合成

在语音信号分析研究的过程中，通过分析语音的发生机理，可将语音信号的形成过程简化为图1的模型。假设激励信号为e(n)表示，语音信号用s(n)表示，则滤波后得到的语音信号s(n)就可以表示为[6]式（7）的形式。

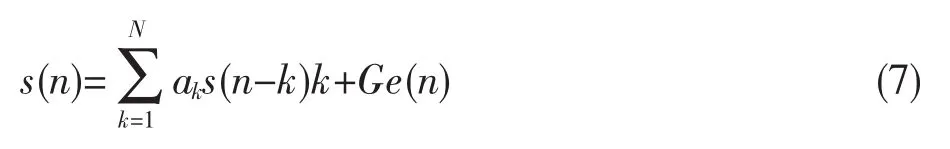
图1 语音信号生成的简化模型

2.1 语音预测

采集到的语音信号的得到是将脉冲序列和声道模型的系统函数进行卷积的过程，由于激励信号e(n)和滤波器的模型V(z)中的系数ai(n)表示，因此这是一个复杂的解卷积的过程。通常激励信号为周期脉冲序列，声道模型中是高斯白噪声序列，两个信号的解卷积，可以使用自相关法或者自协方差法来求解系数ai(n)，并且还Durbin递推算法[7-8]和Schuir递推算法[9]等。

经过相应的方法得到了系数ai(n)，则将图1中的输入和输出对换，就构成了语音的预测模型，并将语音信号e(n)送入预测滤波器中，检测预测语音信号和传输的语音信号的预测残差e(n)，因此e(n)可表示为

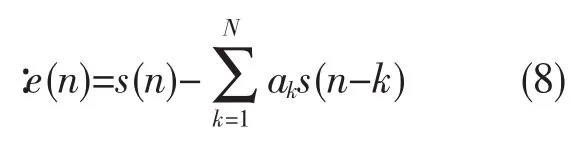
信号的发送和接受端都已知预测系数ai(n)，在发送端只需将误差e(n)发送到接收端，然后将e(n)作为差分方程的激励得到重建的语音信号。在发送端语音信号s(n)是滤波器的输入而误差预测信号e(n)为滤波器的输出，由于语音在短时间内有平稳特性，因此认为预测系数ai(n)不发生变化，不用频繁的传输，可采用线性预测的方法压缩语音数据量，可以大幅度地降低语音信号的带宽。

2.2 语音重构

假设激励信号为x{n}，滤波器系数为ai(n)，则可以利用激励生成重建的语音信号，设重建的语音信号为，可以表示为语音信号在长时间内是非平稳导致预测系数ai(n)是时变的，一般是每10-20 ms就会发生变化，从而产生不同的音节。因此，滤波要根据不同的滤波系数分段进行，相邻两次的滤波必须保持滤波器的状态不发生变化。

2.3 合成语音信号

分析一段10 ms的语音信号，得到它的最佳系数ai(n)，就可以用适当的输入来合成语音，对于浊音信号，以特定的基音频率重复的单位冲激序列作为激励模型；对于清音信号，选择随机噪声和白噪声作为输入，如果不区分清浊语音信号，一般可使用周期激励合成即可。

图2是合成语音信号的系统模拟框图。

图2 分析合成语音的系统模拟框图

抽样的语音信号被分成10 ms的长度，然后对每段数据进行统计分析，计算相邻样点的相关性从而得到最佳的预测系数，语音合成的过程就是将这些预测系数和周期单位冲激系列作为输入，依次得到每段的合成语音。

3 仿真实验

在matlab中编写speechproc.m文件，实现对现有语音的分帧、加窗、线性预测和基音周期提取，在语音信号合成前，先要对系统进行线性预测得到系统的最佳预测系数ai(n)。对每帧语音信号s(n)和预测模型系数ai(n)，用filter计算激励信号e(n)，在系数变化的情况下连续滤波，利用filter的zi和zf参数去维持滤波器的状态不变。如图3所示为模拟声道中的系统特性零极点分布图；图4的语音信号1和语音信号2为模拟原始的语音信号和在信道中传输叠加高斯白噪声的信号；根据计算得到的激励语音信号s(n)和预测模型系数ai(n)，计算重构的合成的语音信号ŝ(n)，并将其与原始的语音信号比较，如图5所示。

对比试听原始的语音信号1和声道中传输的语音信号2以及合成的语音信号，可以明显清晰的听到声道中传输的语音信号2十分模糊，噪声干扰比较大，只能大概听见说话的内容，合成后的信号虽然语音效果不如原始的语音信号1，但是语音质量在可以接受的范围内，说话的内容清楚，偶尔有些“啪，啪”的声音，可能是由于相位的不连续造成的，也可能是波形中的一些毛刺。实验中如果选取激励信号较为简单，在声道中就会丢失很多的信息，合成的语音信号也没有原来的信号内容丰富，经过滤波后可以发现合成后的信号比原来的语音信号有一定的延迟，可能是相位发生了变化导致的，选取样值n取1000-2000，观察3个语音信号，如图6所示。

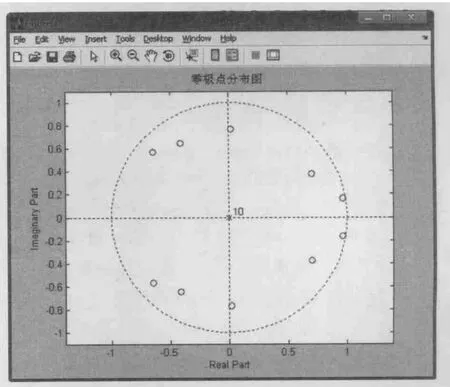
图3 声道的系统特性零极点分布

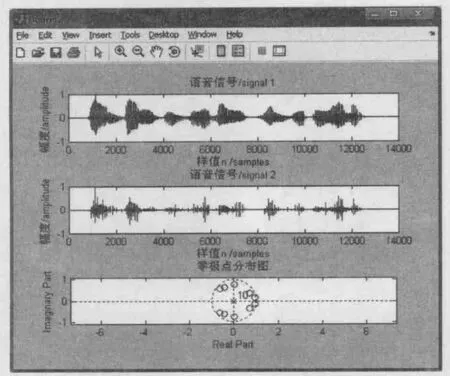
图4 原始的语音信号和在声道中传输的语音信

图5 重构合成的语音信号

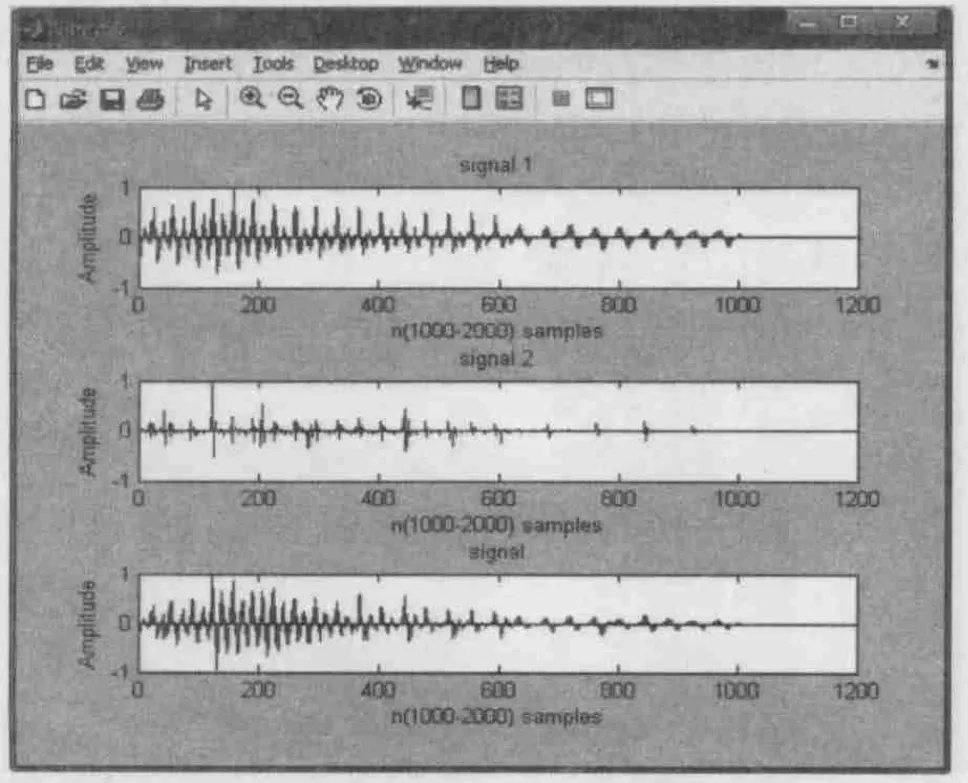
图6 n取1000-2000的3种语音的对

除了该实验基本合成外，还可以试着对原始的语音信号稍做变化，比如变速不变调（改变原始语音信号的抽样速率），其主要应用于消费类电子产品，如英语点读机等；或者变调不变速，不是简单的快进播放，需要通过改变共振频率和基音周期的大小改变音调改变。这两项技术都是以Z变换和线性预测模型为基础的，是语音数字信号处理中的技术。

4 结语

本文分析了语音信号的特点，提出了一种在离散变换域中分析语音信号合成的方法。实验中使用离散系统去模拟声道模型，借助离散系统变换域分析的特点，对语音信号分帧、加窗，进行线性预测和基音周期的提取，从而模拟重构合成语音信号。实验结果表明，该种算法合成的语音信号与原始语音信号非常接近，系统的功能语调，发音风格易于控制，重构精度较高，合成语音准确、生动的传递语音信息，为以后做语音信号处理和可视化的语音视频处理提供一种新的方法。

[1]朱维彬,吕士楠.基于语义的语音合成技术的现状及展望[J].北京理工大学学报,2007,27(5):408-411.

[2]康广玉,郭世泽.基于共振峰过度的协同发音语音合成算法[J].天津大学学报,2010,43(9):810-814.

[3]Thierry Dutoit.High-quality text-to-speech synthesis[J].Journal of Electrical and Electronics Engineering,1997,17(1):25-37

[4]韩纪庆,张 磊,郑铁然.语音信号处理[M].北京:清华大学出版社,2004.

[5]李亚文.基于MATLAB的离散系统分析[J].商洛学院学报,2013,27(4):34-36.

[6]于 驰,王宏伟,宫明龙.多输入多输出离散系统的输出反馈滑模控制[J].东北大学学报:自然科学版,2012,33(2):187-190.

[7]WANG Y Z,ZHANG H G,YANG J.Robust adaptive control for interval time-delay systems[J].Journal of control Theroy and Application,2006,4:367-371.

[8]郭海燕,杨 震.基于近似KLT域的语音信号压缩感知[J].电子与信息学报,2009,31(12):2948-2952.

[9]Chou F C,Seng C Y,Lee L S.A set of corpusbased text-to-speech synthesis technologies for Mandarin Chinese[J].IEEE Transaction on Speech and Audio Processing,2002,10(7):481-494.

[10]张德丰.matlab在数字信号处理中的应用[M].北京:清华大学出版社,2010.