考虑覆盖率下时差式超声流量计的平面声道模型*
刘桂雄 陈国宇 朱斌庚 谭文胜
(1.华南理工大学 机械与汽车工程学院,广东 广州 510640;2.广州柏诚智能科技有限公司,广东 广州 511442)
超声流量计具有计量精度高、管径适应性强、非接触流体、使用方便等特点,其中时差式超声流量计应用最为广泛[1-2].该方法利用声道线平均流速计算管道横截面平均流速,但其声道的覆盖、布置方式直接影响管道横截面平均流速的稳定性,进而影响测量结果的准确性[3-4].目前时差式超声流量计主要有U 型、反射型两种型式,其中U 型超声流量计采用中轴单声道,结构简单,使用方便,但压损大、声道覆盖率低,对流态分布变化的适应性较差[5-6];V型、W 型或“正三角形”型等反射型超声流量计的压损较小,但其声道均布置在同一平面上或空间对称分布,声道覆盖率非常低[7-9].为解决该问题,文中研究了一定声道覆盖率下声道段覆盖方式所需的声道段数,再根据声道段数确定超声流量计的声道空间拓扑结构.
1 立体声道平面声道模型的特性分析
在设计立体声道平面声道模型之前,先讨论其几个特性:①声道模型的对应性;②流场的对称性;③绕中轴的旋转不变性.考虑到超声流量计常应用于长直圆形管道,文中以长直圆形流体模型为研究对象[10].图1 为立体(3D)声道模型及其平面(2D)声道模型示例,声道(超声波在流体中的传播路径)与管壁存在多个交点,单条声道由一段或多段声道段(相邻两交点间的声道部分)组成.声道模型的对应性是指一个立体声道模型具有对应平面声道模型(声道在管道横截面上投影),即立体声道模型与平面声道模型有直接关系,声道覆盖与平面声道模型相关,声道实现方式与立体声道模型有关.
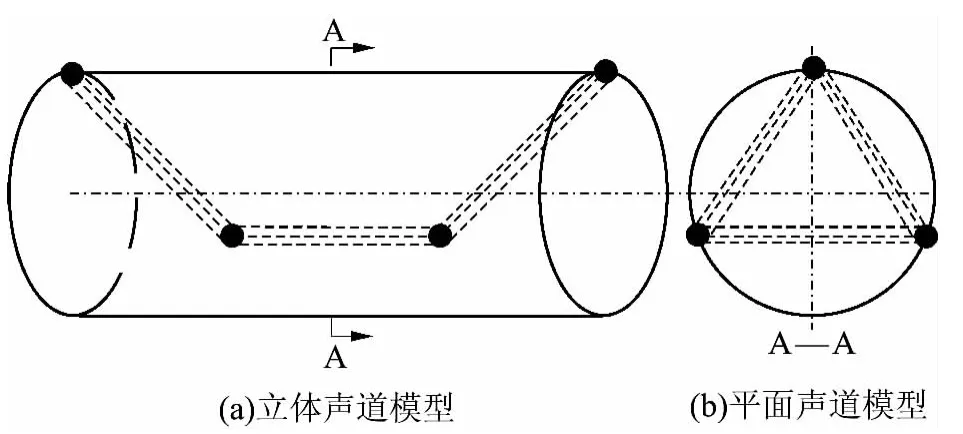
图1 立体声道模型及其平面声道模型示例Fig.1 Example of 3D ultrasonic track model and its 2D ultrasonic track model
图2 为一般长直圆形管道的流速分布图,管道内流速呈现“中心高-四周低”式分布[11],设流体沿管道各横截面处流量均匀,则在长直圆形管道横截面流场分布与径向距离有关,流场具有对称性[12].
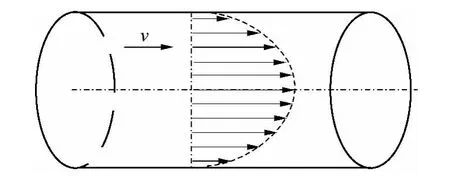
图2 长直圆形管道的流速分布Fig.2 Velocity profile in straight circular pipe
由于横截面内流场关于任一直径对称,故覆盖横截面半圆区域的声道,就可以认为截面全覆盖.同时,声道段绕管道截面中心旋转任意角度前后的覆盖区域流场分布相同,故可通过旋转变换将平面声道模型各声道段旋转至相互平行位置,如图3 所示,旋转前的平面模型等效于旋转后的平面模型.其中,第i 段声道段的中心线与管道横截面中心的距离为d(i).
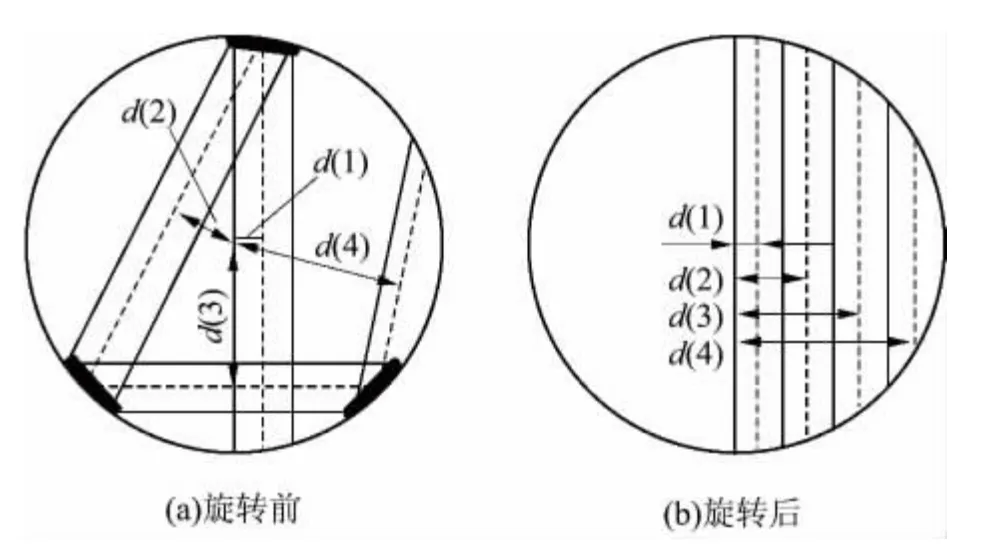
图3 平面声道模型旋转前后示意图Fig.3 Schematic diagrams of 2D ultrasonic track models before and after rotation
2 立体声道平面声道模型计算方法
令声道段的中心线至管道横截面中心距离由近至远,经旋转变换后平面声道模型的声道段依次记为1,2,…,Nsum.若第1 段声道段边界过横截面中心,则d(1)等于声束半径Rub.设Rpip为管道半径,Ssum为声道覆盖总面积,则声道覆盖率ζ 满足

2.1 不同声道覆盖方式下覆盖面积的计算
根据相邻声道段间重叠的不同,旋转变换后平面声道模型可分为重叠覆盖、完全覆盖、不完全覆盖3 种方式(见图4).平面声道模型的声道覆盖总面积Ssum由多段声道段组成,由两扇形面积相减得到第i 段声道段的面积显然,不同覆盖方式下的覆盖面积公式也有所差异.
设在半圆内重叠覆盖、完全覆盖、不完全覆盖的声道段数分别为Nolc、Ncc、Nucc,则满足d(i +1)-d(i)<2Rub的重叠覆盖方式时,

满足d(i+1)-d(i)=2Rub的完全覆盖方式时,
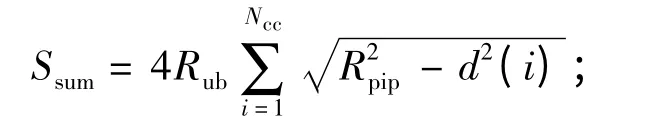
满足d(i+1)-d(i)>2Rub的不完全覆盖方式时,
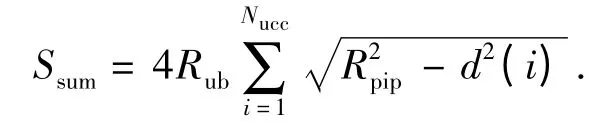

图4 平面声道模型的3 种覆盖方式Fig.4 Three covering modes of 2D ultrasonic track model
2.2 声道段数的约束条件
显然,在管径大小一定的情况下,声道段数Nsum由覆盖率ζ、覆盖方式决定.覆盖方式不同,覆盖总面积Ssum也就不同,因覆盖总面积Ssum还与覆盖率ζ直接相关,故声道段数Nsum仅与覆盖率ζ 间存在约束关系.
设声道段i 的中心线投影与其顶点所在半径构成的夹角为φpro_V(i),则对于重叠覆盖方式,有
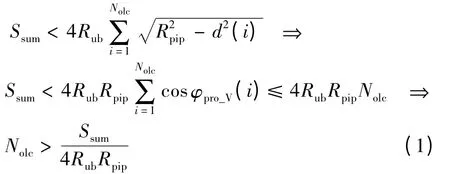
通常Rpip、Rub已知,所要求的覆盖率ζ 确定,故Nsum的范围也可确定.
2.3 声道段中心线至横截面中心的距离
确定Nsum的范围后,就可以按照一定规律(如等差)来确定声道段i 的中心线至横截面中心的距离d(i),这是声道段位置的重要参数[13].若d(i)符合等差数列(公差Δdas)规律,则d(i)分布满足等差数列时分布律为
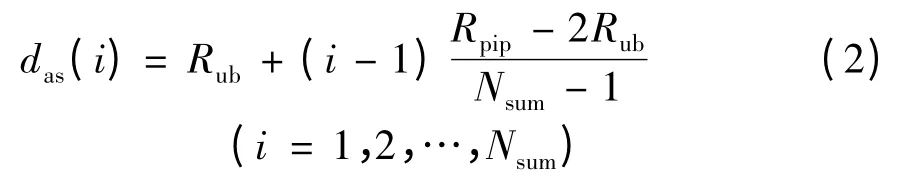
可以看出,das(i)的设计简单,计算量小.
2.4 平面声道模型参数的设计
求得d(i)后,需还原旋转前声道模型.为减小超声信号在传播过程中的衰减,当声道段i、j 连续时,要求相邻声道段中心线投影的夹角αpro(i,j)尽量小[14],0 <αpro(i,j)≤60°为宜,首尾连接两声道段存在同侧(在同一半圆上)或异侧(不在同一半圆上)分布情况.图5 为同侧相邻声道段夹角的计算示意图(图中i <j).
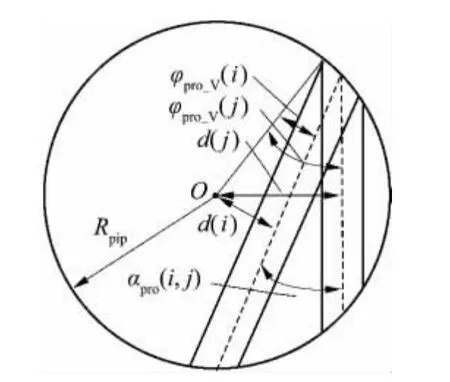
图5 同侧相邻声道段夹角的示意图Fig.5 Schematic diagram of angles of adjacent ultrasonic track segments on the same side
在声道段i、j 同侧下,设声道段i 的中心线投影与其顶点所在半径构成的夹角为φpro_V(i),那么由正弦定理得
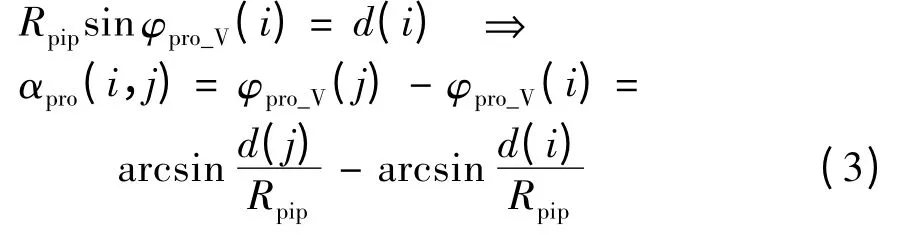
由
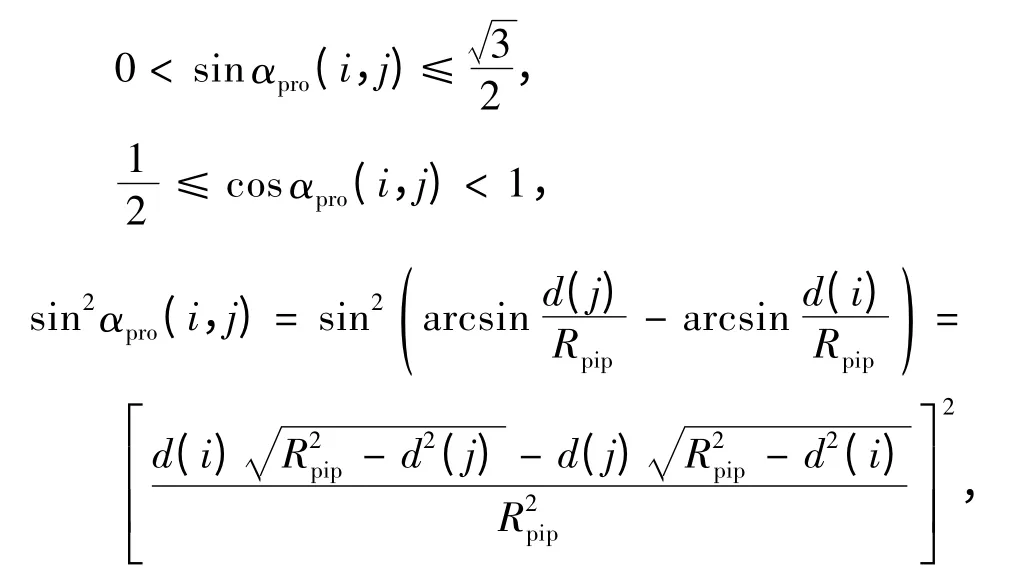
可得

因此,若d(i)、d(j)满足式(4),则声道段i、j 符合同侧分布.同理,声道段i、j 异侧时,可得
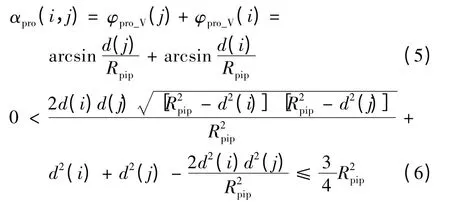
即若d(i)、d(j)满足式(6),则声道段i、j 符合异侧分布.
需强调的是,因超声波在传播过程中存在衰减,故单条声道反射次数(即声道段数)不宜过多[15].若声道段数Nsum≤4,则可采用单声道平面声道模型(SP-2DUT),否则采用多声道平面声道模型(MP-2DUT).因声道段排列结果多样,故MP-2DUT 通常不唯一,设计更为复杂,所得模型也比SP-2DUT 复杂得多.
3 设计算例
由于重叠覆盖方式应用较少,故文中设计算例重点选择完全覆盖、不完全覆盖方式.
算例1 管道半径Rpip=18 mm、声束半径Rub=3 mm、覆盖率ζ=1,由式(1)得Nsum=3 ≤4,采用SP-2DUT模型;为使声道段分布均匀,声道段中心线与横截面中心的距离das(i)采用等差数列规律.由式(2)得
das(i)= 6i -3, i= 1,2,3.
根据式(4)、(6)判断相邻两声道段同、异侧分布,并由式(3)、(5)分别计算符合同、异侧分布的相邻声道段夹角αpro-同侧(i,j)、αpro-异侧(i,j),进而可求得5 种合理的平面声道模型方案:
(1)αpro-异侧(1,2)=39.6°,αpro-同侧(2,3)=26.4°;
(2)αpro-同侧(1,2)=20.4°,αpro-同侧(2,3)=26.4°;
(3)αpro-同侧(1,3)=46.9°,αpro-同侧(3,2)=26.4°;
(4)αpro-同侧(2,1)=20.4°,αpro-同侧(1,3)=46.9°;
(5)αpro-异侧(2,1)=39.6°,αpro-同侧(1,3)=46.9°.
以方案①为例,其平面声道模型及旋转后示意图如图6 所示.算例2 管道半径Rpip=60 mm、声束半径Rub=3 mm、覆盖率ζ=0.5,由式(1)得Nsum=5>4,需采用MP-2DUT 模式,das(i)采用等差数列规律.同理可算出表1 所示的相邻声道段同、异侧判别及夹角.
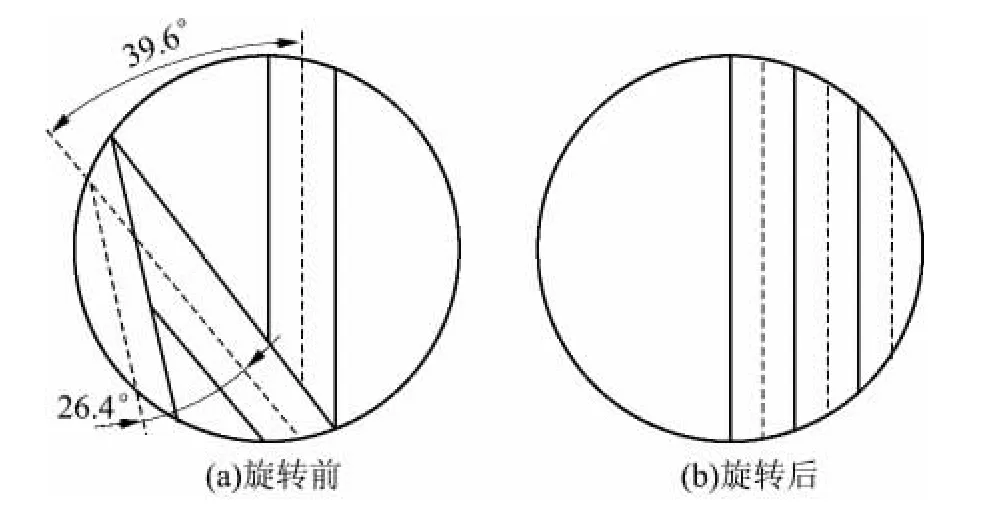
图6 方案①的平面声道模型及旋转后示意图Fig.6 Schematic diagrams of 2D ultrasonic track models of scheme ①before and after rotation

表1 相邻声道段的同、异侧判别及夹角1)Table 1 Ipsilateral and contralateral discriminations and angles of adjacent ultrasonic track segments (°)
鉴于MP-2DUT 模式需先将声道段1 至声道段5 组合成两条声道,使各声道的声道段数小于4.声道段的组合要根据表1 的同、异侧判别及夹角.其中一种组合方案为:声道段1、2 组成一条声道,声道段3、4、5 组成另一条声道,组合后各声道设计方法与SP-2DUT 模式相同.该组合下可求得6 种合理的平面声道模型方案:
(1)αpro-异侧(1,2)=18.8°,αpro-同侧(3,4)=16.5°,αpro-同侧(4,5)=25.3°;
(2)αpro-异侧(1,2)=18.8°,αpro-同侧(3,5)=41.8°,αpro-同侧(5,4)=25.3°;
(3)αpro-异侧(1,2)=18.8°,αpro-同侧(4,3)=16.5°,αpro-同侧(3,5)=41.8°;
(4)αpro-同侧(1,2)=13.1°,αpro-同侧(3,4)=16.5°,αpro-同侧(4,5)=25.3°;
(5)αpro-同侧(1,2)=13.1°,αpro-同侧(3,5)=41.8°,αpro-同侧(5,4)=25.3°;
(6)αpro-同侧(1,2)=13.1°,αpro-同侧(4,3)=16.5°,αpro-同侧(3,5)=41.8°.
4 结语
(1)时差式超声流量计的立体声道模型与平面声道模型直接相关,声道覆盖直接影响平面声道模型的分布,研究考虑声道覆盖率下时差式超声流量计的立体声道平面声道模型非常重要.
(2)在长直圆形管道横截面上,流场分布仅与径向距离有关,若声道覆盖横截面半圆区域,则可实现横截面全覆盖;声道段绕截面中心旋转任意角度前后,覆盖区域的流场分布相同,可通过旋转变换将平面声道模型各声道段旋转至相互平行位置.
(3)半圆内平面声道模型声道段总数Nsum由覆盖率ζ、管道半径Rpip、声束半径Rub确定,即Nsum>由于Rpip、Rub已知,所要求的覆盖率ζ 确定,故Nsum的范围也确定.(4)确定Nsum的范围后,就可以按照一定规律(如等差)来确定声道段i 的中心线至横截面中心的距离d(i),等差数列规律das(i)设计简单,计算量小;求得d(i)后,需还原变换前的声道模型,为减小超声信号在传播过程中的衰减,当声道段i、j 连续时,要求相邻声道段中心线投影的夹角αpro(i,j)尽量小;首尾连接两声道段存在同侧(在同一半圆上)或异侧(不在同一半圆上)分布情况,相邻声道段中心线投影夹角αpro(i,j)的同、异侧分布与d(i)、d(j)、管道半径Rpip有关.(5)由于超声波在传播过程中存在衰减,单条声道反射次数(声道段数)不宜过多.平面声道模型分为单声道平面声道模型SP-2DUT、多声道平面声道模型MP-2DUT.声道段排列结果呈多样性,MP-2DUT 的设计更复杂,其模型比SP-2DUT 复杂得多.
[1]Lynnworth L,Liu Y.Ultrasonic flowmeters:half-century progressreport,1955—2005 [J].Ultrasonics,2006,44(Suppl 1):1371-1378.
[2]Ding Fenglin,Li Zongliang,Wei Yanming,et al.Design of high-accuracy ultrasonic flowmeter[J].Aerospace Control and Application,2011,37(1):28-30.
[3]Jacobson S.New developments in ultrasonic gas analysis and flowmetering[C]∥Proceedings of 2008 IEEE International Ultrasonics Symposium.Beijing:IEEE,2008:508-516.
[4]Yeh T,Espina P,Osella S A.An intelligent ultrasonicflowmeter for improved flow measurement and flow calibration facility[C]∥Proceedings of IEEE Instrumentation and Measurement Technology Conference.Budapest:IEEE,2001:1741-1746.
[5]Tang Jingyuan,Chen Jianming,Ma Hongbin,et al.Numerical analysis of flow field characteristics in three-Zshaped ultrasonic flowmeter[J].Applied Mechanics and Materials,2012,226/227/228:1829-1834.
[6]Kuang Weihua,Pang Xufeng.Flow characteristics study of transit time ultrasonic flowmeter based on fluent[J].Advances in Information Sciences and Service Sciences,2012,4(21):413-421.
[7]Zhao Wenming,Shao Xianhe,Wang Ling,et al.Research on the influencing factors to ultrasonic flow measurement[J].Process Automation Instrumentation,2012,33(9):80-82.
[8]Yeh T T,Espina P I.Special ultrasonic flowmeters for insitu diagnosis of swirl and cross flow[C]∥Proceedings of 2001 ASME Fluids Engineering Division Summer Meeting.New Orleans:ASME,2001:1-8.
[9]Mahadeva D V,Baker R C,Woodhouse J.Studies of the accuracy of clamp-on transit time ultrasonic flowmeters[C]∥Proceedings of IEEE Instrumentation and Measurement Technology Conference.Victoria:IEEE,2008:969-973.
[10]JJG1030—2007,超声流量计检定规程[S].北京:中国计量出版社,2007.
[11]Franchini S,Sanz-Andre's A,Cuerva A.Measurement of velocity in rotational flows using ultrasonic anemometry:the flowmeter[J].Experiments in Fluids,2007,42(6):903-911.
[12]Bezdek M,Landes H,Rieder A,et al.A coupled finiteelement,boundary-integral method for simulating ultrasonic flowmeters[J].IEEE Transactions on Ultrasonics,Ferroelectrics and Frequency Control,2007,54(3):636-646.
[13]李拥军,敖道敢.一种快速近似模式匹配算法[J].华南理工大学学报:自然科学版,2012,40(6):103-108.Li Yong-jun,Ao Dao-gan.A fast algorithm for approximate pattern matching[J].Journal of South China University of Technology:Natural Science Edition,2012,40(6):103-108.
[14]张红虎,郑卫.临街高大厂房噪声引起的街道声场的仿真模型[J].华南理工大学学报:自然科学版,2012,40(6):145-151.Zhang Hong-hu,Zheng Wei.Simulation model of sound field in street space caused by noise transmitted from bordering large workshop buildings[J].Journal of South China University of Technology:Natural Science Edition,2012,40(6):145-151.
[15]Martin Treiber,Kim Jin-Yeon,Jacobs Laurence J,et al.Correction for partial reflection in ultrasonic attenuation measurements using contact transducers[J].Journal of the Acoustical Society of America,2009,125(5):2946-2953.

