细长型液压启闭机液压缸筒活塞杆挠度的计算分析*

丁问司 张旭 范亚军

(华南理工大学 机械与汽车工程学院，广东 广州 510640)

液压启闭机是水利工程中的重要设备，它通过活塞杆的推拉完成各类水工闸门的开启与关闭［1-2］.液压启闭机中的活塞杆作为长细比较大的受压杆件，其挠度对液压缸的纵向受压稳定性有着至关重要的影响，是机构设计中的关键问题.

目前，工程上使用较多的液压缸挠度计算方法主要有等截面杆计算法和阶梯杆计算法两类［3］.等截面杆计算法是将活塞杆与缸体看作固接在一起且截面相同的杆件，按欧拉公式进行稳定性计算.该方法因通常情况下的液压缸缸体与活塞杆截面并不相等且缸体与活塞杆的抗弯断面惯性矩差别较大而导致算出的临界载荷大大偏低.阶梯杆计算法是将液压缸视为一般的变截面实心简支梁，活塞杆段的截面特性取活塞杆的实际面积特性，缸体段的截面特性取液压缸壁的截面特性，按欧拉公式进行稳定性计算.由于活塞杆与缸体并非固接，液压缸在轴向压力作用下产生横向弯曲时，其受力状况与固接杆也明显不同，因而这两种计算方法得到的结果与实际情况均存在较大偏差.文献［4-6］在阶梯杆计算模型基础上考虑了缸头密封间隙以及活塞与缸壁间隙对缸筒－活塞杆挠度产生的影响，并采用该模型对三峡船闸人字门启闭机液压缸的稳定性进行了理论分析与试验研究.文献［7］在传统阶梯杆静力模型基础上考虑液压油对液压缸稳定性的影响，提出了液压缸的动力学模型，并对承受动态载荷作用的液压缸稳定性进行了讨论，研究结果表明液压油在高压下对保持缸筒和活塞杆直线形状有益，相比阶梯杆模型，采用该模型算出的静力稳定值显著增加.文献［8］中采用有限元方法对液压缸临界载荷进行了计算和最优设计，为工程应用提供了参考.文献［9］针对缸筒活塞杆的偏心对液压缸负载能力的影响进行了理论分析和试验研究，结果表明，即使是采用阶梯杆模型进行液压缸挠度计算，得到的结果与实际情况仍然存在偏差.

1 液压缸活塞杆挠度的计算模型

1.1 间隙引起的液压缸挠度

在液压启闭机液压缸中，缸筒与活塞杆连接处、活塞与缸壁之间的间隙会导致缸筒、活塞杆在承载时产生几何变形［10］，如图1 所示.

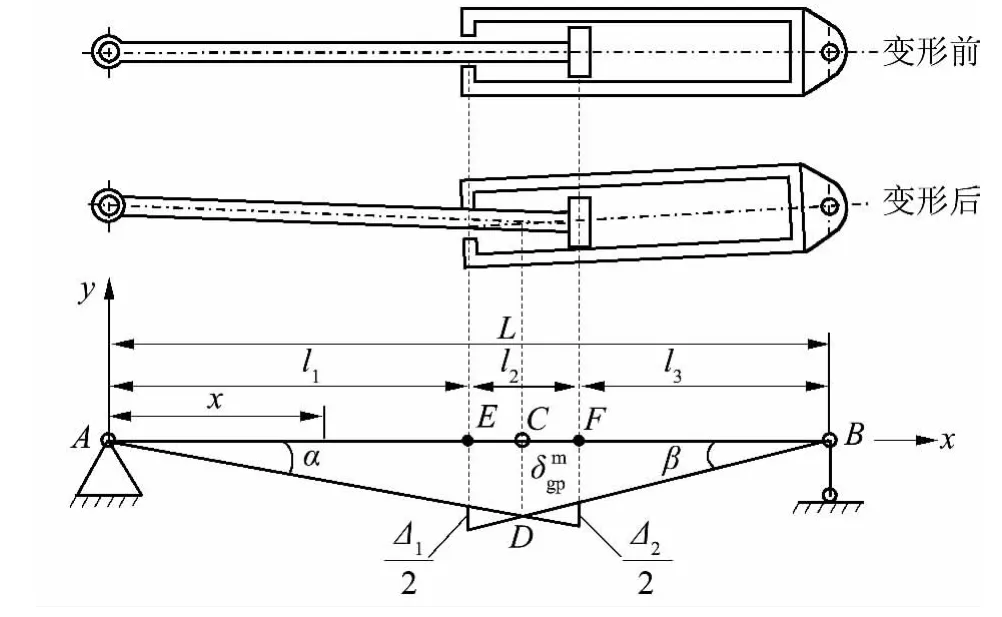
图1 液压缸间隙引起的挠度示意图Fig.1 Schematic diagram of deflection caused by cylinder gap

图1 中A 为闸门吊耳部位，B 为缸筒端部支座，C 为液压缸最大挠度发生处，E 为导向套中心点，F为活塞中心点;AD 为活塞杆轴线，BD 为缸体轴线，CD 为液压缸最大挠度，l1为活塞杆外伸段长度，l2为液压缸导向长度，l3为缸体段计算长度，L 为吊耳到液压缸端部支座的间距，Δ1为缸头密封间隙，Δ2为活塞与缸壁处密封间隙，δmgp为间隙引起的最大挠度，α 和β 分别为活塞杆和缸筒因间隙而形成的与水平方向的夹角.

对于倾斜布置的液压缸，由间隙引起的液压缸挠度与水平布置时的情况相同，计算方法如下:

由间隙引起的最大挠度为

在横坐标为x 处，由间隙引起的挠度为

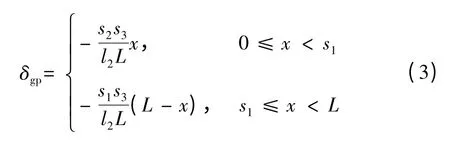
1.2 载荷与自重引起的液压缸挠度

根据液压启闭机液压缸的结构和工作特点，可得到轴向载荷与自重引起的挠度计算模型，如图2所示.缸筒内压力油简化为仅承受压力的二力杆，缸筒视为与活塞杆能相对滑动但不能相对转动的梁，它只承受弯矩［11］.

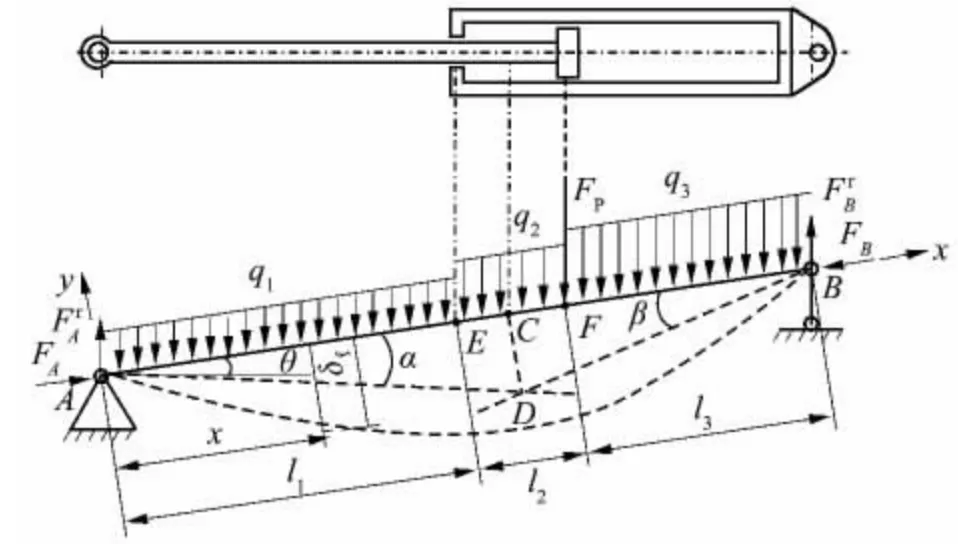
图2 液压缸受力示意图Fig.2 Schematic diagram of force for hydraulic cylinder

图2 中θ 为液压缸与水平面的安装夹角，q1、q2、q3分别为活塞杆、液压缸有杆腔和无杆腔的单位长度重力(考虑油液质量)，FA、FB分别为闸门吊耳和液压缸底座沿缸体轴线方向的支反力，FP为活塞的重力，分别为液压缸两端沿竖直方向的支反力，δf为横坐标x 处杆件弹性变形引起的挠度.由图2 可得

精致的火把烧尽，参星已对着房门。 今晚是怎样的晚上，看见这样艳丽的美人。 你呀，你呀，该把这个美人怎么办。[4]109-110

缸筒及活塞杆各截面处的弯矩为

为简化计算，忽略缸筒－活塞杆轴向变形，并考虑到在当前工况下有FA=FB=F(F 为液压缸中油压力)，则缸筒－活塞杆挠度的微分方程为［12］

式中，E1、E2、E3分别为缸筒－活塞杆在外伸段、导向段和缸体段的弹性模量，I1、I2、I3分别为缸筒－活塞杆在外伸段、导向段和缸体段的抗弯断面惯性矩.

求解可得δf1、δf2、δf3的解析表达式:

代入边界条件与连续条件

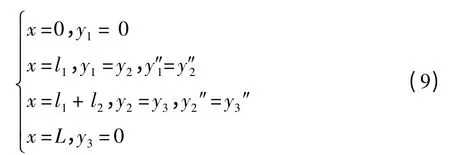
可求出系数C1，C2，…，C6.

考虑结构的连续性，令y'1=y'2=y'3= 0，可解出缸筒－活塞杆3 个区域的最大挠度，比较后便可得到缸筒－活塞杆最大挠度的发生位置及大小.

1.3 液压缸总挠度

综合考虑由间隙引起的液压缸挠度和由载荷与自重引起的液压缸挠度，联立式(3)、(8)，可得到缸筒－活塞杆的挠度方程:

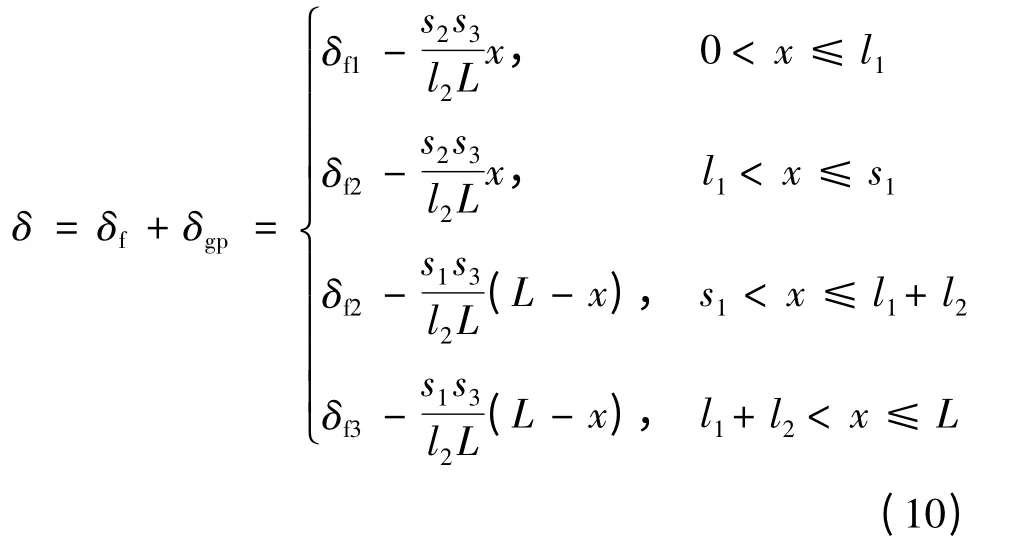
2 工程实例

某大型水电站使用的液压启闭机液压缸参数如下:在活塞杆完全伸出情况下，启闭机液压缸及活塞杆全长L=24075 mm，其中活塞杆长l1=11975 mm，液压缸长l3=11490 mm，导向长度l2=610 mm;液压缸内径为520 mm，外径为605 mm，活塞杆直径为240 mm;启闭机液压缸的轴线与水平面夹角θ=68°;缸头密封间隙Δ1=0.2 mm，活塞与缸壁间隙Δ2=0.2 mm;活塞杆材料为1Cr17Ni2，许用应力为550 MPa;缸体材料为Q345B，许用应力为295 MPa;弹性模量为2.1×105MPa;其他参数如下:q1=3.480 N/mm，q2=4.872 N/mm，q3=7.547 N/mm，F=2 MN.

代入实际数据，由式(7)、(8)可求得通项系数分别为:C1=0.010 6，C2=－0.050 1，C3=－0.0735，C4=0.3197，C5=－0.174 6，C6=0.386 4.最大挠度(为138.0 mm)发生在x=9.2782 m 处，油液质量对最大挠度各组成部分的影响如表1 所示，缸筒－活塞杆的挠度解析计算结果如图3(a)所示.

当缸筒－活塞杆的θ=0°(即水平放置)时，最大挠度发生在x=9.1100 m 处，最大挠度为316.4 mm.安装角度对最大挠度各组成部分的影响如表2 所示.

表1 油液质量对最大挠度组成部分的影响Table 1 Influence of oil mass on components of the maximum deflection mm

表2 安装角度对最大挠度组成部分的影响Table 2 Influence of installation angle on components of the maximum deflection

图3 θ=68°且考虑油液质量时的缸筒－活塞挠度曲线Fig.3 Deflection curves of cylinder and piston rod with θ is 68° and consideration of oil mass

在Solidworks 中建立缸筒－ 活塞杆的三维模型［13-18］，使用其Simulation 模块进行网格划分与有限元求解，分析结果如图3(b)所示.从图可知，θ=68°且考虑油液质量时，有限元计算得到最大挠度发生在9.5930 m 处，最大挠度为138.7 mm.

3 结论

(1)液压启闭机液压缸的缸筒－活塞杆挠度包括由间隙引起的初始挠度和载荷与自重引起的附加挠度，其中载荷与自重是导致挠度的主要因素，间隙是引起挠度的次要因素.

(2)当活塞杆行程较长时，随着油液质量/液压缸总质量比值的增加，其对挠度的影响不可忽视.

(3)考虑计算载荷与自重引起的附加挠度时，液压缸的安装角度对挠度有着重要的影响.因此，按照水平或垂直布置的工况进行计算的缸筒－活塞杆挠度，对倾斜作业的液压缸并不适用.

［1］Brown William D.Lock gates and operating equipment［Z］.Washinton D C:US Army Corps of Engineers，1994.

［2］Karbhari V M，Rivera J，Dutta P K.Effect of short-term freeze-thaw cycling on composite confined concrete ［J］.Journal of Composite for Construction，2000，4(4):191-197.

［3］林荣川，魏莎莎.基于小挠度曲线微分方程的液压缸稳定性分析［J］.长江大学学报:自然科学版，2009，6(4):280-282.Lin Rong-chuan，Wei Sha-sha.Analysis of the stability of the hydraulic cylinder based on small deflection curve differential equation ［J］.Journal of Yangtze University:Natural Science Edition，2009，6(4):280-282.

［4］郭应龙，陶亦寿.大型卧式液压缸的挠曲与稳定性计算原理及软件研究［J］.武汉水利电力大学学报，1996，29(6):99-103.Guo Ying-long，Tao Yi-shou.Research of deflection and stability calculation principle and software of the large horizontal hydraulic cylinder［J］.Engineering Journal of Wuhan University，1996，29(6):99-103.

［5］郭应龙，陶亦寿.三峡船闸人字门启闭机液压缸的挠度与纵压稳定性计算［J］.水利电力机械，1996，18(5):7-10.Guo Ying-long，Tao Yi-shou.Calculation of deflection and vertical-pressured stability of three gorges ship lock miter gate hoist hydraulic cylinder［J］.Water Conservancy ＆Electric Power Machinery，1996，18(5):7-10.

［6］陶亦寿，魏文炜.大型卧式液压油缸挠度与稳定性计算［J］.长江科学院院报，1998，15(5):24-27.Tao Yi-shou，Wei Wen-wei.Deflection and stability calculation of the large horizontal hydraulic cylinder［J］.Jour-nal of Yangtze River Scientific Research Institute，1998，15(5):24-27.

［7］顾迪民，康亚东，孙景惠.液压油缸的动力稳定性分析［J］.哈尔滨建筑大学学报，1996，29(3):79-85.Gu Di-min，Kang Ya-dong，Sun Jing-hui.Dynamic stability analysis of the hydraulic oil cylinder［J］.Journal of Harbin University of Architecture and Engineering，1996，29(3):79-85.

［8］林荣川，郭隐彪，魏莎莎，等.液压缸临界载荷计算和最优设计［J］.中国机械工程，2011，22(4):389-393.Lin Rong-chuan，Guo Yin-biao，Wei Sha-sha，et al.Critical load and optimum design for hydraulic cylinders［J］.China Mechanical Engineering，2011，22(4):389-393.

［9］Gamez-Montero P J，Salazar E，Castilla R，et al.Misalignment effects on the load capacity of a hydraulic cylinder［J］.International Journal of Mechanical Sciences，2009，51(2):105-113.

［10］兰朋，陆念力，刘曼兰.长细液压油缸的稳定性计算模型探讨［J］.建筑机械，2004，24(6):87-88.Lan Peng，Lu Nian-li，Liu Man-lan.Stability calculating model of slim hydraulic cylinder［J］.Construction Machinery，2004，24(6):87-88.

［11］刘礼华，陈五一，魏晓斌，等.大型液压启闭机油缸活塞杆的计算分析研究［J］.工程力学，2010，27(4):185-189.Liu Li-hua，Chen Wu-yi，Wei Xiao-bin，et al.Calculation and analysis on the large-scale hydraulic hoist cylinder piston［J］.Engineering Mechanics，2010，27(4):185-189.

［12］Karbhari V M，Asce M.Response of fiber reinforced polymer confined concrete exposed to freeze and freeze-thaw regimes［J］.Journal of Composite for Construction，2002，6(1):35-40.

［13］陈鹏霏，孙志礼，滕云楠，等.往复式压缩机活塞杆可靠性分析与参数化设计［J］.东北大学学报:自然科学版，2009，30(9):1310-1313.Chen Peng-fei，Sun Zhi-li，Teng Yun-nan，et al.Reliability analysis and parametric design of piston rod of a reciprocating compressor［J］.Journal of Northeastern University:Natural Science，2009，30(9):1310-1313.

［14］Shabana A A，Bauchau O A，Hulbert G M.Integration of large deformation finite element and multibody system algorithms［J］.Journal of Computational and Nonlinear Dynamics，2007，2(4):351-359.

［15］Mao C，Ricles J，Lu L W，et al.Effect of local details on ductility of welded moment connections［J］.Journal of Structural Engineering，2001，127(9):1036-1044.

［16］Johannes G.A 3D finite element method for flexible mutibody systems ［J］.Muhibody System Dynamics，2006，15(4):305-320.

［17］Markovets A V，Mazin L S.Study of dynamics of variable structure lever mechanisms ［J］.Journal of Machinery Manufacture and Reliability，2008，37(3):213-220.

［18］Ham A T.Finite-element simulation of the elliptical cup deep drawing process by sheet hydro forming［J］.Finite Elements in Analysis and Design，2007，43(3):234-246.