伪随机信号(m序列)相关辨识的动态测试方法
何华锋,李元凯,董海迪,杨学猛
(第二炮兵工程大学302室,陕西 西安 710025)
0 引 言
随着测试技术的发展,人们对航空航天领域伺服系统动态测试的准确性与快速性提出了更高的要求。传统动态测试采用相关函数法[1],其测试过程如下:首先利用计算机控制交流D/A模件向被测系统加一定频率的正弦信号,利用中速A/D采集响应输出,由计算机进行相关函数运算,求出该频率点的幅频和相频特性。测试中需要测量的频率点有6个,而一个频率点需要测量3个周期[2],因此整个测试完成需要18个周期(约120s),不仅测试时间较长,而且仅得到6个频率点的测量值。
本文针对航空航天领域伺服系统的动态性能测试要求,提出一种基于伪随机信号相关辨识的动态测试新方法。
1 伪随机信号相关辨识的动态测试方法
由于该测试方法是针对线性定常离散系统的,实际工程中可选用伪随机二位式序列——m序列(周期信号)作为测试激励信号[3],整体结构如图1所示。图中 η(t)为输入噪声,ξ(t)为输出观测噪声。假设整个系统中的采样周期或步长与输入m序列的步长Δ之比为1∶3,且假设输入信号x(t)与噪声η(t)、ξ(t)均为零均值的平稳随机过程,彼此统计独立。
首先利用数字计算机提供m序列m(k),经过数模转换加到被测对象的输入端;然后将输出响应y(t)经模数转换后得到y(k),送到计算机进行实时递推计算,经若干周期后得到脉冲响应序列;最后利用Hankel矩阵法可以估算出被测系统的传递函数,从而得出被测对象的幅频、相频特性。

图1 离散系统动态特性相关辨识法结构图
2 m序列的自相关函数
在推导基于m序列离散形式相关辨识的计算公式之前,先说明一下m序列自相关函数的形式。可以证明,m序列自相关函数[4]为
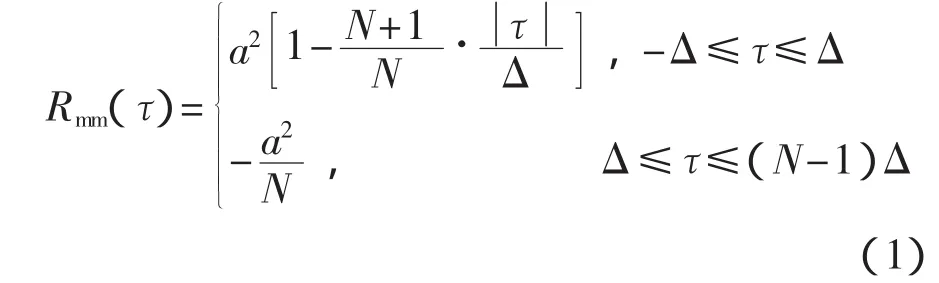
式中:a——m序列逻辑状态“0”对应的输出正电压的幅值;
N——m序列一个周期的总拍数;
Δ——移位脉冲的周期。
由于离散化,可将式(1)简化为[5]
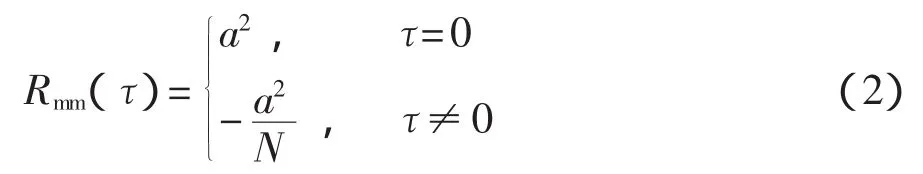
3 基于伪随机信号相关辨识的动态测试原理
3.1 脉冲响应序列递推公式
对于图1所示的被测对象,根据卷积定理公式有

式中:g(σ)——被测对象的脉冲响应。
若将被测对象的动态方程写成内部描述形式,有

当 x(0)=0 时,有
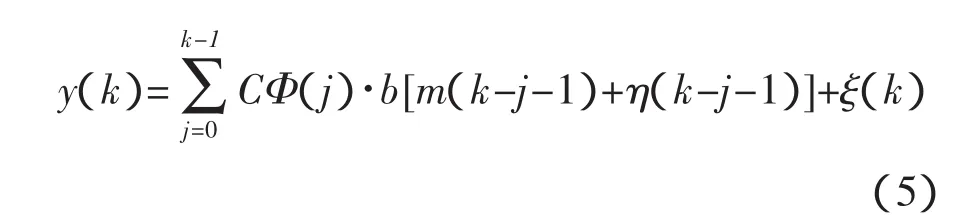
可知:Φ(j)b=g(j),将式(5)改写为

设N为m序列一个周期的总拍数,且NΔ=T大于脉冲响应衰减到零的时间,将式(6)代入y(k)与m(k)的互相关函数,可得

式(7)中Rmm(σ)为m序列的自相关函数,这就是维纳-霍普夫方程的离散形式。
取 σ=1,2,3,…,N,得
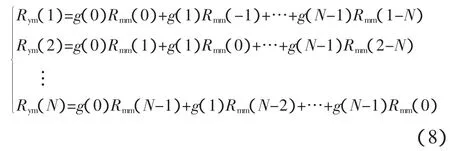
写成矩阵形式,有
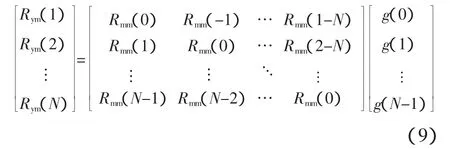
则有
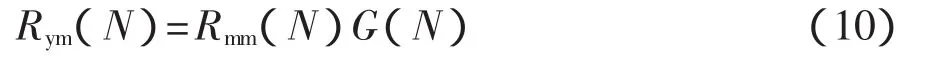
其中
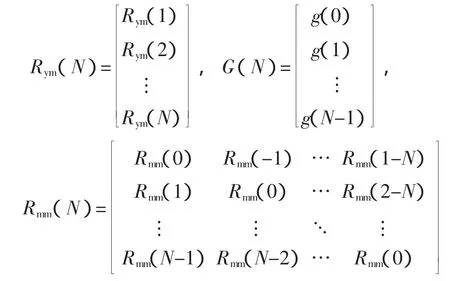
根据式(2)可得

因此

由式(12)可知,只要得到输入输出的互相关函数向量Rym(N),就可以利用其求出被测系统的脉冲响应G(N)。然而,Rym(1)、Rym(2)、…、Rym(N)不易直接精确求出,且为了能够实现在线辨识,下面推导求脉冲响应G(N)的递推公式。
根据第M次的测量,可按式(13)来估算输入输出的互相关函数
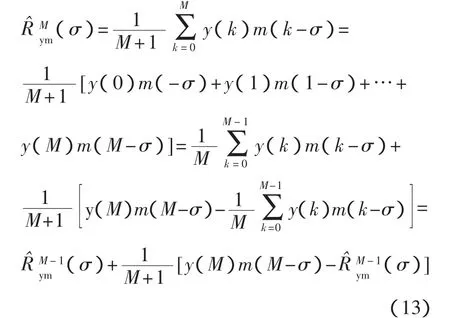
将式(13)代入式(12),可得第M次测量估算出的系统脉冲响应序列G^M(N)。

则有:
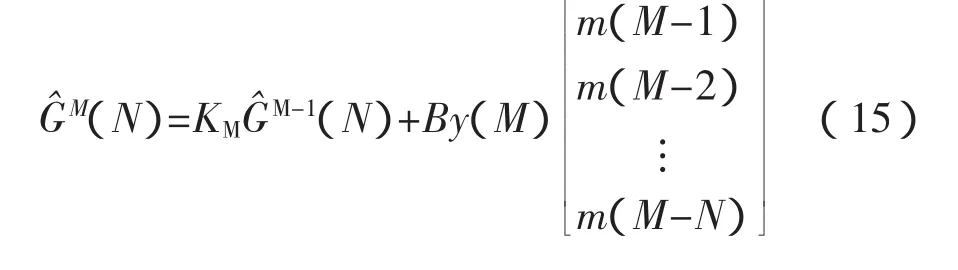

3.2 序列的参数选择
以上讨论了利用离散条件下伪随机信号(m序列)相关辨识的方法对被辨识系统的脉冲响应序列进行估计的理论依据。在实际辨识中,需要根据被辨识系统动态性能的先验知识,确定m序列的参数Δ、N和a[6]。通过分析m序列的自相关函数和功率谱密度可知:其自相关函数不是一个理想的周期脉冲,且功率谱密度也不是常值。但如果被辨识系统的工作频带处于(0~2π/3)Δ范围之内,则可以将m序列近似看作理想的周期白噪声。因此,设被辨识系统的最高工作频率为ωmax,动态响应时间为ts,其参数应满足ωmax<2π/(3Δ),且NΔ=(1.2~1.5)ts。
3.3 由脉冲响应确定传递函数的Hankel矩阵法
通过输入伪随机信号m序列,采样输出的响应信号进行实时的递推计算,得到被测对象的脉冲响应序列的估计值。本节运用Hankel矩阵法[7],利用脉冲响应的估计值来计算得出被测对象的脉冲传递函数系数的估计值。
设被辨识的离散系统模型是一个n阶的脉冲传递函数

将式(16)化为相应的状态转移方程
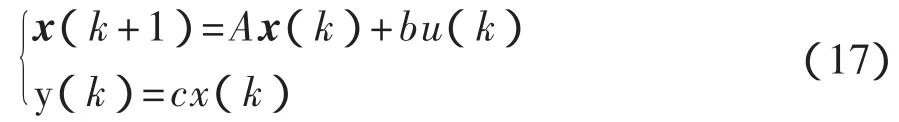
其脉冲传递函数又可以表示为

又因为

为互逆关系,则
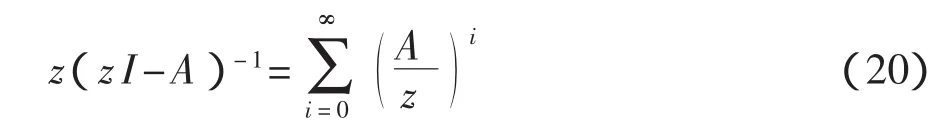
将式(20)两边同时除以z,可得
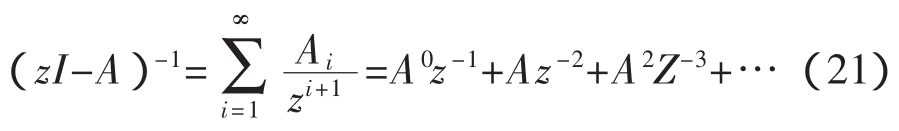
等式右边取前n项代入式(18),可得脉冲传递函数与脉冲响应的关系式

将式(20)代入式(16)中,可得
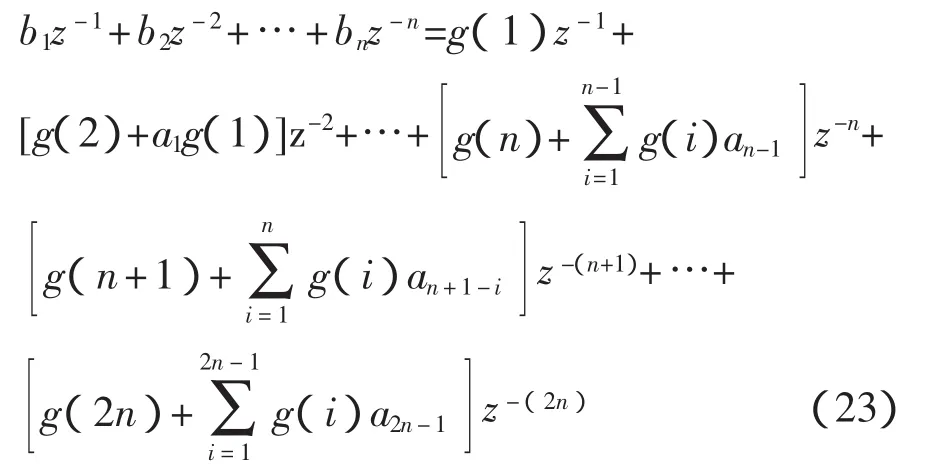
比较式(23)等号两边z的同幂次项系数可得
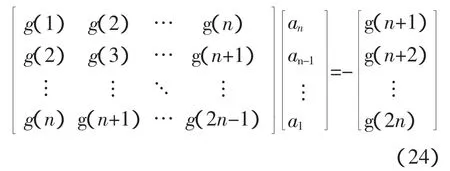
以及
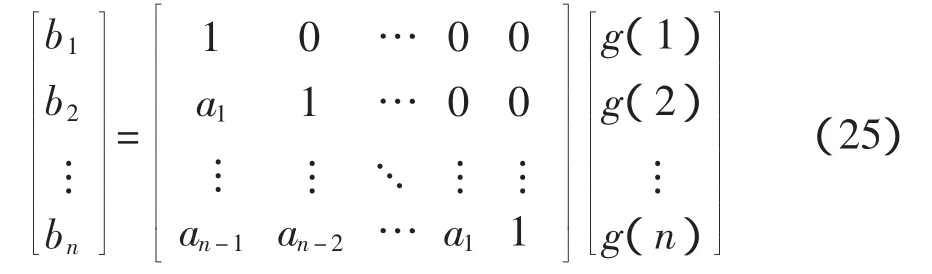
根据Hankel矩阵的定义可知,式(24)左边的矩阵是一种待定的 Hankel矩阵,记作 H(n,l)。因此,将基于m序列相关辨识得到的被测对象的脉冲序列响应估计值代入式(24)和式(25)中,便可求得脉冲传递函数的估计值;经双线性变换,可以得到连续传递函数的估计值;由估计的传递函数可求得幅频和相频特性[8],完成动态测试。
4 验证实验
本节将利用基于伪随机相关辨识的动态测试方法对传递函数标准化(即传递函数已知且固定)仪器设备的动态性能进行测试。实验结果给出了被测对象的幅频与相频特性。
4.1 实验模型
实验模型结构如图1所示,设整个系统中的采样周期或步长与输入m序列的步长Δ之比为1/3。已知被测系统的传递函数模型为

4.2 实验参数
设被测系统最高工作频率为1/5,动态响应时间为10s,则Δ的选择范围小于10.472s,若选Δ=1.5s,则可得N>10,选N=15。因此,输入的m序列的周期T为22.5s,a值取0.5mA,系统采样时间T0为0.5s,试验进行3个m序列的周期(68s)。
4.3 实验结果
运用该新方法经过3个m序列周期的测试后,递推得到的被测系统脉冲响应序列数据如表1所示。
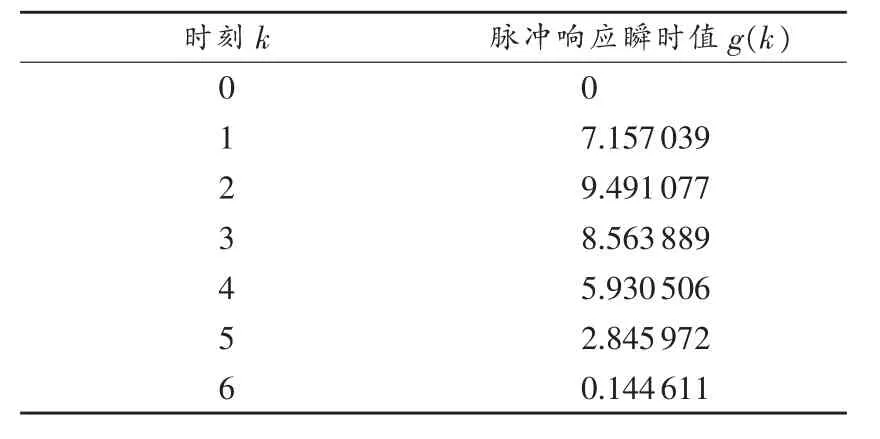
表1 脉冲响应序列数据(T0=0.5s)
由于被测系统的阶数是3,构造的Hankel矩阵如下:
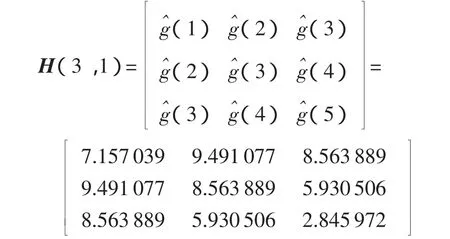
分别求得:

可得被测系统的脉冲传递函数的估计值为
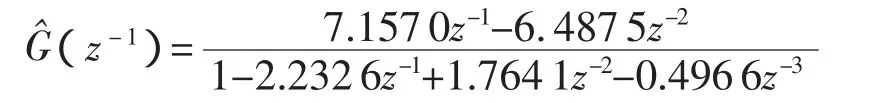
经双线性变换后,连续传递函数的估计值为
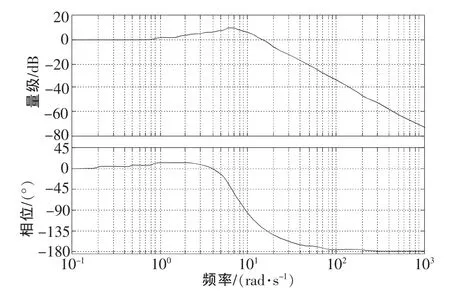
图2 被测对象的对数频率特性(Bode图)
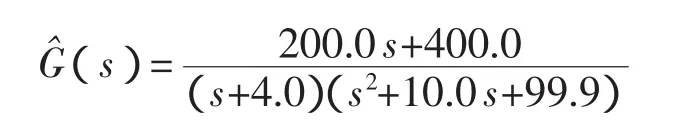
可见,估计的传递函数与标准化仪器的实际传递函数非常接近。根据估计传递函数可进一步求得被测对象的幅频与相频特性,如图2所示。
5 结束语
由上述实验结果可知,该方法在已知被测系统阶数的情况下,可以获得较好的近似传递函数;该方法运用于仪器设备的动态测试,可以准确地得到其幅频与相频响应;另外,传统的动态测试方法需用时大约120s,使用该新方法可以节约用时约52s。
[1]崔吉俊.火箭导弹测试技术[M].北京:国防工业出版社,1999.
[2]胡昌华,马清亮,郑建飞.导弹测试与发射控制技术[M].北京:国防工业出版社,2010.
[3]王然冉,赵德平.用伪随机信号相关辨识检测线路的频率参数[J].沈阳工业大学学报,1998(20):46-49.
[4]李白男.伪随机信号在工业系统辨识中的应用[M].北京:科学出版社,1987.
[5]赵淑清,郑薇.随机信号分析[M].哈尔滨:哈尔滨工业大学出版社,1999.
[6]王志贤.最优状态估计与系统辨识[M].西安:西北工业大学出版社,2004.
[7]方崇智,萧德云.过程辨识[M].北京:清华大学出版社,1988.
[8]卢京潮.自动控制原理[M].西安:西北工业大学出版社,2009.

