汽车排烟余热回收强化换热管的数值模拟与分析

徐承隆，刘伟军，胡伟平

(1.上海工程技术大学汽车工程学院，上海 201620；2. 上海工程技术大学机械工程学院，上海 201620)

管道的强化对流换热技术普遍应用于能源动力、汽车、石化等很多领域。现在，新型强化换热管一直是强化换热的研究热点。强化换热目的在于节能降耗、降低成本，因此提高换热设备传热效果有重要意义[1]。

常见的强化换热管有内插旋流片管[2-3]、翅片管[4]、缩放管[5]和内肋管等[6-8]。其中，不连续双斜向内肋管是根据对流换热中纵向涡强化换热理论和场协同理论开发的一种新型强化换热元件，与其他强化管相比，其在高雷诺数对流传热区域是一种性能较好的强化换热管。交叉内肋换热管主要依靠圆管表面加工成型某种涡流发生器[9]，即采用凸起表面使换热表面附近产生纵向涡，从而扰动管壁附近的热边界层，达到增强换热的目的。文献[7]和文献[8]研究了管外水、管内水或润滑油的对流换热，其采用圆角矩形式的内肋形状，而本文则针对管内烟气与管外水对流换热，并采用了一种新的流线型换热表面，依靠凸起表面产生的壁面纵向涡，探求换热管的结构参数对湍流换热性能的影响，对其结构参数进行了优化，并用场协同知识分析其强化换热的原因。

1 换热管结构

不连续双斜向内肋换热管，最早由清华大学过增元、孟继安等学者[6]提出。笔者研究了一种双斜向流线型内肋强化换热管(double-inclined streamline ribs tube，简称DISR tube)。

图1为双斜向流线型内肋强化换热管示意图，图2为其流线型的内肋结构示意图。由于流线型内肋前圆后尖，表面光滑，略像水滴的形状。因此，其在流体中运动时受到阻力较小，有利于在保证强化换热的同时不至于增加过大的阻力。流线型内肋的排布特点是在内壁面形成了许多不连续的、和管轴线的一定角度并向两个方向倾斜的条状内肋。

图1 双斜向流线型内肋换热管Fig.1 Diagram of DISR tube

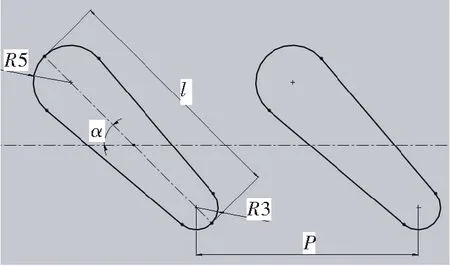
图2 双斜向流线型内肋管的内肋Fig.2 Streamlined ribs of DISR tube

本文研究的双斜向流线型内肋换热管的有效换热长度为500 mm，基管尺寸为Φ63 mm× 1.5 mm，换热管内径di为60 mm，材质为不锈钢。其结构参数如表1所示。

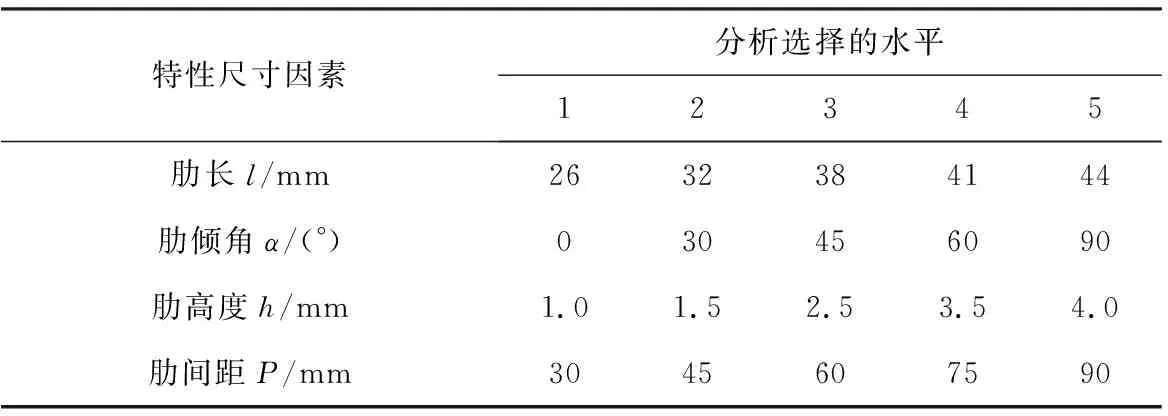
表1 双斜向流线型内肋管特性尺寸Tab.1 Characteristic dimension of the DISR tube

2 数值模拟计算模型与条件

2.1 几何模型

选取整根换热管进行数值计算，利用CATIA完成建模，网格划分使用ANSYS/ICEM-CFD生成，数值计算则用ANSYS/FLUENT完成。为提高换热管近壁面处热边界层的计算精度，管壁附近采用棱柱型网格进行边界层加密，管中心区域采用四面体非结构性网格，并在网格划分时对全局网格进行平滑光顺处理。图3为该模型的截面处网格划分效果图，图4为管壁面网格图。

图3 截面处网格Fig.3 Grid at outlet cross section

图4 管壁面网格Fig.4 Grid of the tube wall

2.2 边界条件

假定在等壁温边界条件下流动和换热的周期性充分发展条件已满足。计算条件：管内介质为烟气[10]，其物性参数选择如下：wCO2=13%，wO2=11%，wN2=76%，ρ=0.617 kg/m3，Cp=1.122kJ/(kg·℃)，λ=0.048 4W/(m·℃),Pr=0.65，μ=2.82×10-5Pa·s。管外是冷却水，设定内管壁温度Tw=443K，烟气进口温度Tf=623K，出口边界选用outflow选项。烟气流速参考汽车尾气流速分别取10,15,20,25,30，40m/s。

对于高雷诺数区(Re=1.2×104～5×104)，采用分离变量法隐式求解，保证收敛的稳定性；标准k-ε湍流模型，压力和速度的耦合采用SIMPLEC算法；动量、能量的求解采用QUICK格式，湍动能和湍流扩散率的求解采用二阶迎风格式；定义收敛条件为质量和能量计算残差绝对值分别达到1×10-5和1×10-6精度。

2.3 网格独立性验证

取普通圆管进行网格独立性验证，选取网格数386 241和844 826，在相同Re数下计算的努塞尔数Nu和摩擦阻力系数f，与通过Gnielinski和Filonenko经验公式计算得到的Nu和f对比。如表2所示，两种网格数下的模拟结果均在10%误差以内，故可认为两种网格数用于仿真分析是可信的。

表2 网格独立性验证Tab.2 Mesh independent verification

3 数值模拟结果与分析

3.1 管内对流换热规律

在双斜向流线型内肋管内，流体在内肋的作用下将形成强烈的多纵向涡流，且该涡流主要出现在管壁附近。这些涡是沿管轴向螺旋式前进的，这将有效扰动热边界层，改善管内温度场和流场的协同作用[7]，从而增强换热管的换热性能。

在l=30 mm,P=60 mm,h=2.5 mm,α=45°和Re=1.2×104(即流速约10 m/s)的情况下，对双斜向流线型内肋管内部流场和温度场分布进行数值模拟研究。图5和图6分别表示双斜向流线型内肋管和普通圆管横截面处的流场。图7和图8分别是双斜向流线型内肋管和普通圆管中横截面处的温度场。

通过比较可看出，图5中双斜向流线形内肋管在截面处出现了4个纵向涡，涡流的出现对图中箭头所指处附近的壁面进行冲刷，增强45°,135°,225°，315°近壁处附近的径向扰动，减小热边界层厚度，于是表面换热系数增强，强化换热效果增强。相比图6的普通圆管，其内部几乎没有径向流动，缺少热边界层扰动，其换热效果不够理想。

比较图7和图8可知，对于普通圆管的对流换热，截面等温线为圆形，而对于双斜向流线型内肋管，管内流体温度梯度在-45°～45°和135°～225°两个近壁区域内沿径向变化较大，并在图7中的箭头所指处，等温线最为密集，这与普通圆管相比，近壁面温度梯度更大，使得管壁表面换热系数提升，因此其较大程度地强化了对流换热。

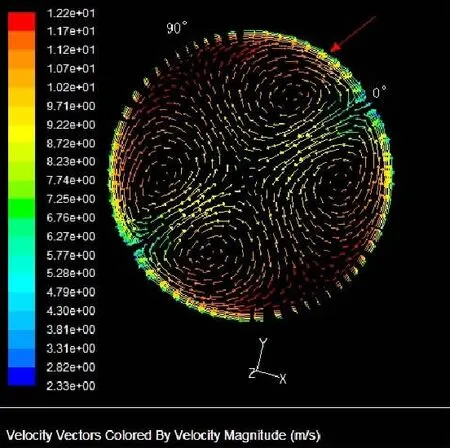
图5 双斜向流线型内肋管横截面流场Fig.5 Flow structure in DISR tube

图6 普通圆管横截面流场Fig.6 Flow structure in plain tube

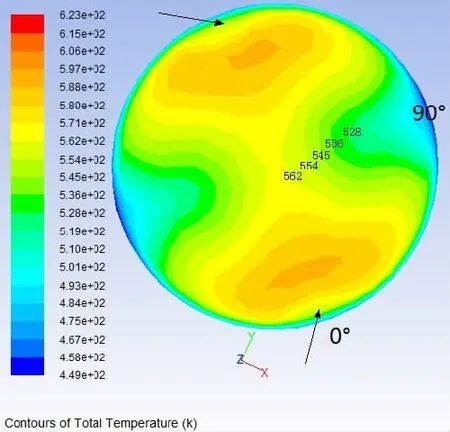
图7 双斜向流线型内肋管横截面温度场分布Fig.7 Isotherms in the DISR tube

图8 普通圆管横截面温度场分布Fig.8 Isotherms in plain tube

3.2 参数优化

在强化换热的研究中，努赛尔数Nu、摩擦阻力系数f、同功耗强化指标(performance evaluation criteria，以下简称PEC)是分析强化换热效果好坏的主要指标[11]。

PEC=[(Nus/Nu0)/(fs/f0)1/3]。

(1)

式(1)中：Nus和Nu0分别为强化换热管和光管的努赛尔数；fs和f0分别为强化换热管和光管摩擦阻力系数。

图9-图12分别为内肋长度、肋倾角、肋高度和肋间距对换热评价指标PEC的影响分析。

图9 肋长对换热效果的影响Fig.9 PECs influenced by various ribs length

图10 肋倾角对换热效果的影响Fig.10 PECs influenced by various ribs inclined angle

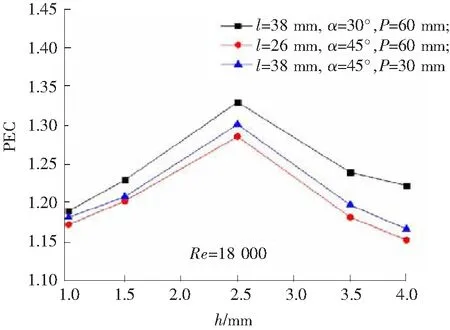
图11 肋高度对换热效果的影响Fig.11 PECs influenced by various ribs height

图12 肋间距对换热效果的影响Fig.12 PECs influenced by various ribs pitch

3.2.1 肋长对换热效果的影响

Re=1.8×104的情况下，从图9中可以看出，当肋间距、肋倾角、肋高度都变化时，随着肋长的增加，同功耗强化指标PEC均呈先升后降的趋势。

肋长增加将影响烟气侧的表面换热系数和管内摩擦阻力系数。在肋长为28～38 mm时，管内近壁面热边界层的扰动逐渐加剧，管径向扰流的流速增大，近壁面温度梯度增大，提升了表面换热系数，所以换热得到增强，PEC值上升；而在肋长为38～44 mm时，随肋长的继续增加，表面换热系数提升幅度较小，摩擦阻力系数增加较多，PEC值下降。肋长存在最优值约为38 mm。

3.2.2 肋倾角对换热效果的影响

Re=1.8×104的情况下，从图10可以看出，当肋间距、肋长、肋高度都变化时，随着肋倾角的增加，同功耗强化指标PEC均呈先升后降的趋势。

肋倾角主要影响其引导出纵向涡的剧烈程度。在肋倾角从0°增加到45°的过程中，角度的增加使内肋引导出较为剧烈的纵向涡，纵向涡引发管径向强烈的扰动改善了管内温度场和速度场的协同作用，于是换热效果得到增强；然而在肋倾角从45°增加到90°的过程中，一方面摩擦阻力系数增幅较换热的增幅更多，另一方面肋倾角过大并不利于纵向涡的产生，所以换热效果减弱。肋倾角存在最优值约为45°。

3.2.3 内肋高度对换热效果的影响

Re=1.8×104的情况下，从图11可以看出，当肋间距、肋长、肋倾角都变化时，随着肋高度的增加，同功耗强化指标PEC均呈先升后降的趋势。

随着肋高度的增加，管内烟气侧表面换热系数和管内摩擦阻力增加。在肋高度为1～2.5 mm时，纵向涡逐渐形成，肋高度的增加增强了近壁面涡流的湍流强度，从而提升烟气侧表面换热系数，增强对流换热，PEC值上升；在肋高度2.5～4 mm时，随着肋高度的增加，一方面由于纵向涡略微向管中心偏移，使得近壁面的湍流强度略微下降，热边界层扰动程度下降，强化换热效果下降，另一方面内肋的继续增加使得摩擦阻力增加较快，而烟气侧换热系数提升幅度较少，此时换热效果减弱，PEC值下降。肋高度最优值约为2.5 mm。

3.2.4 肋间距对换热效果的影响

Re=1.8×104的情况下，从图12可以看出，当肋长、肋倾角、肋高度都变化时，随着肋间距的增加，同功耗强化指标PEC均呈先升后降的趋势。

肋与肋间距的大小主要体现在每一对由内肋引导出的纵向涡在流动方向上能保持的距离。当间距为30～60 mm时PEC值逐渐上升，此时由于肋间距过小导致前一个纵向涡还未消失就流到了下一个内肋，纵向涡未得到最大化利用；而在肋间距为60～90 mm时，由于肋间距过大导致纵向涡在流到下一个内肋前已经消失，纵向涡未能覆盖整根换热管，所以PEC值开始下降[8]。肋间距存在最优值约为60 mm。

3.3 性能对比

根据上述分析，取最佳值尺寸参数，即肋长30 mm(0.5di)、肋倾角45°、肋高度2.5 mm(0.041 7di)、肋间距60 mm(di)为研究对象，分析其在高雷诺数区(Re=1.2×104～5×104)时的强化换热和摩擦阻力规律。

图13和图14分别表示管内Re与Nu，f的关系。普通圆管的湍流Nu和f按Gnielinski经验公式计算[12-13]。普通圆管Nu和f的仿真值和经验值相比，误差分别在4.17%和25.8% 以内，Nu误差较小，而f偏差较大，可能与壁面粗糙度设置或所选湍流模型有关，但作为数值模拟该结果尚可接受。 其中，由图13和图14可知，Re=1.2×104～5×104时，双斜向流线型内肋管与普通圆管相比，Nu可增加54.5%～90.7%，f增加157.6%～204.2%。由图15可知，同功耗强化指标PEC值均呈现下降趋势，当取最佳尺寸时，PEC最大值可达1.396。

图13 双斜向流线型内肋管的传热性能Fig.13 Heat transfer performance of the DISR tube

图14 双斜向流线型内肋管的阻力性能Fig.14 Flow performance of the DISR tube

图15 几种尺寸综合换热评价对比Fig.15 PECs for several enhanced tubes

图16 DISR与两种管型的PEC值对比Fig.16 PECs for DISR tube and two enhanced tubes

如图16所示，DISR换热管(l=38mm,α=45°,P=60mm,h=2.5mm)、管内插线圈[14](e/di=0.06,P/di=1)和螺旋槽管[15](h/di=1/22, P/di=0.727)相比，在Re=2×104～5×104上DISR管的同功耗换热强化评价指标PEC和其余两种管型曲线趋势相同且较其他两种管型更高，即DISR管有更好的强化换热效果。

3.4 场协同分析

近年来，清华大学学者过增元等曾提出用场协同理论来重新审视对流换热的本质，并引入了场协同角的概念以此说明对流换热中速度场和温度场协同程度的好坏[16-18]。

(2)

式(2)在场协同的计算中又可写成

(3)

式(3)中：Vx，Vy和Vz分别是流场速度矢量在x，y和z方向上的分量；而∂T/∂x，∂T/∂y和∂T/∂z分别是温度梯度在x，y和z方向上的分量。

使用FLUENT的场函数指令(Customer Field Function)设置式(3)的函数关系，对模拟结果中流场速度矢量分量Vx，Vy，Vz和温度梯度分量∂T/∂x，∂T/∂y，∂T/∂z进行提取，在模拟结果的基础上计算其场协同角，导出记录场协同角的结果文件，导入Matlab绘制场协同角的散点图。

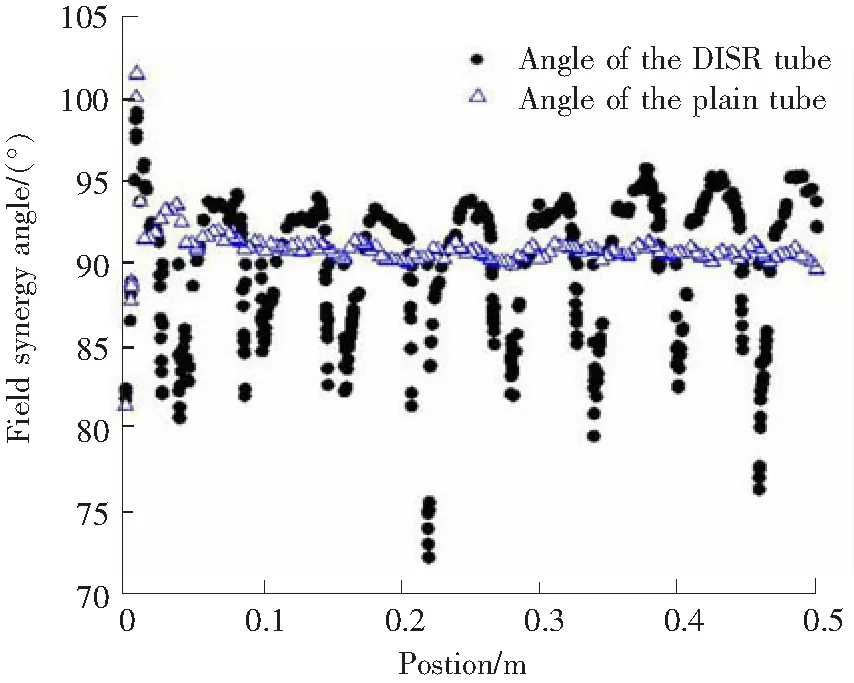
图17 普通圆管和DISR管内场协同角分布图Fig.17 Field synergy angles in the plain tube and in the DISR tube

如图17所示为普通圆管和DISR管内壁面附近沿管轴向的协同角分布图。可见，在整根普通圆管上，流体温度梯度和速度矢量之前的夹角大致分布在90°左右，由于入口段效应，仅在入口处的场协同角变化幅度较大。此时流线方向几乎与管道轴向平行。根据场协同理论，由于速度矢量与温度梯度方向所成的角接近90°时二者的协同效果较差，此时强化换热效果较不理想。然而，对于DISR换热管，由于流线型内肋产生剧烈的涡对使管内温度梯度方向与流速方向的夹角变小，尤其是在流线型内肋附近，场协同角已从90°左右减小到了80°左右。图17中，DISR管内的场协同角呈现出类似周期性脉冲变化，场协同角在每一个内肋附近都会出现一次骤减的突变，可见流线型内肋对于场协同角的影响显著。管内流体在遇到每一个内肋后都会产生较剧烈的涡，流体流向改变的同时也改变了流场速度矢量和温度梯度矢量的夹角，使得温度梯度场与速度场的协同效果得到了改善，从而达到强化换热效果。

4 结 论

1) 对双斜向流线型内肋换热管在管内烟气管外水的湍流换热进行了数值模拟研究。结果表明，在流线型内肋的作用下，流体在管内壁面附近将形成较强烈的纵向涡，扰动热边界层。

2) DISR管内的场协同角呈现出类似周期性脉冲的变化，场协同角在每一个内肋附近都会出现一次骤减的突变，可见流线型内肋对于场协同角的影响显著，场协同角从90°减少到80°，使得温度梯度场与速度场的协同效果得到了改善，换热能力得到增强。

3)数值优化表明，双斜向流线型内流换热管的肋长、肋倾角、内肋高度和肋与肋间距都存在最优值，分别为38 mm，45°，2.5 mm和60 mm。

4)在Re=1.2×104～5×104时，双斜向流线型内肋管努赛尔数Nu可增加54.5%～90.7%，摩擦阻力系数f增加157.6%～204.2%，同功耗强化指标PEC值随Re增加呈现下降趋势，其最大值可达1.396。

参考文献/References:

[1] WEBB R L. Principles of Enhanced Heat Transfer[M]. NewYork: John Wiley & Sons，1994.

[2] EIMSAARD S，THIANPONG C，PROMVONGE P. Experimental investigation of heat transfer and flow friction in a circular tube fitted with regularly spaced twisted tape elements[J]. Int Commun Heat Mass Transfer，2006，33: 1225-1233.

[3] 杨汝仲，邓先和. 管内插入旋流片的流动和传热的数值模拟[J]. 化学工程，2010，38(6): 23-25.

YANG Ruzhong，DENG Xianhe. Numerical simulation of flow and heat transfer inside tube with regularly spaced twisted-tapes[J]. Chemical Engineering, 2010，38(6): 23-25.

[4] ZHANG Z，YU Z，FANG X. An experimental heat transfer study for helically flowing outside petal-shaped finned tubes with different geometrical parameters[J]. Appl Therm Eng，2007，27:268-272.

[5] 黄维军，邓先和，周水洪. 缩放管强化传热机理分析[J]. 流体机械，2006，34(2):76-79.

HUANG Weijun，DENG Xianhe，ZHOU Shuihong. Mechanism of heat transfer enhancement for converging-diverging tube[J]. Fluid Machinery，2006，34(2): 76-79.

[6] LI Xiaowei，MENG Ji'an，GUO Zengyuan. Turbulent flow and heat transfer in discrete double inclined ribs tube[J]. International Journal of Heat and Mass Transfer ，2009，52: 962-970.

[7] 孟继安，李志信,过增元.不连续双斜向内肋强化换热管性能[J].化工学报，2005，56(6): 995-998.

MENG Ji'an，LI Zhixin，GUO Zengyuan. Performance of enhanced heat transfer tube with discrete double-inclined ribs[J]. Journal of Chemical Industry and Engineering，2005，56(6): 995-998.

[8] 李晓伟,严 环,孟继安,等.不连续双斜向内肋管纵向涡流动显示[J].工程热物理学报，2006，27(sup2): 119-121.

LI Xiaowei，YAN Huan，MENG Ji'an. Flow visualization of the longitudinal vortices in the discrete double inclined ribs tube[J]. Journal of Engineering Thermophysics，2006，27(sup2): 119-121.

[9] BERGLES A E. ExHFT for fourth generation heat transfer technology[J]. Experimental Thermal and Fluid Science，2002，26: 335-344.

[10] 华建社，朱 军，李小明,等. 冶金传输原理[M]. 西安：西北工业大学出版社，2005.

HUA Jianshe，ZHU Jun，LI Xiaoming,et al. Metallurgy Transport Principle[M]. Xi'an: Northwestern Polytechnical University Press，2005.

[11] 李志信，过增元. 对流传热优化的场协同理论[M].北京：科学技术出版社，2010.

LI Zhixin，GUO Zengyuan. The Field Synergy Theory of Convection Heat Transfer Optimization[M]. Beijing:Science Press，2010.

[12] GNIELINSKI V. New equations for heat and mass transfer in turbulent pipe and channel flows[J]. Int Chem Eng, 1976，16(2): 359-368.

[13] GNIELINSKI V. Single-phase Convective Heat Transfer[M]. New York: Hemisphere，1983.

[14] GARCIA A，VICENTE P G，VIEDMA A. Experimental study of heat transfer enhancement with wire coil inserts in laminar-transition-turbulent regimes at different prandtl numbers[J]. Heat Mass Transfer，2005，48(21/22): 4640-4651.

[15] 吴慧英,帅志明,周强泰.凝结换热器采用螺旋槽管的强化传热研究[J]. 化工学报，1997，48(5)：626-630.

WU Huiying，SHUAI Zhiming，ZHOU Qiangtai. Investigation on heat transfer enhancement of the condensation heat exchanger with spirally corrugated tubes[J]. Journal of Chemical Industry and Engineering，1997，48(5): 626-630.

[16] GUO Z Y， LI D Y，WANG B X. A novel concept for convective heat transfer enhancement[J]. Heat Mass Transfer，1988，41(14)：2221-2225.

[17] TAO W Q，GUO Z Y，WANG B X. Field synergy principle for enhancing convective heat transfer：Its extension and numerical verifications[J]. Heat Mass Transfer，2002，45(18): 3849-3856.

[18] 过增元. 对流换热的物理机制及其控制：速度场与热流场的协同[J]. 科学通报，2000，45(19): 2118-2122.

GUO Zengyuan. The physical mechanism and control of convective heat transfer:the velocity field and temperature field synergy[J]. Science Bulletin, 2000，45(19): 2118-2122.