一种基于任务分解的时间均衡调度算法

魏妮妮，宋 翌

(武汉生物工程学院计算机与信息工程系,湖北武汉 430415)

随着大型的科学研究对高性能和大容量数据处理能力需求的不断增加，网格计算技术的研究范围迅速扩大。网格计算的实质就是分布式计算，且主要研究在分布、异构、自治的网络资源环境上动态构建虚拟组织并实现跨自治域的资源共享与协同工作。任务调度是网格计算研究的核心问题之一，并已证明是NP完全问题，它引起了众多学者的关注[1-4]。

网格任务调度实质就是按照一定的调度策略和调度规则，把用户提交的网格作业映射到多管理域资源上的过程[5]。围绕网格计算中的任务调度问题，国内外已经做了大量的研究工作，先后提出了各种任务调度算法[6-7]。其中比较经典的有Min-min算法、Max-min算法、Sufferage算法、Max-int算法、SA算法和遗传算法等。另外就是这些算法的组合算法，如文献[8]—文献[11]提到的算法。这些算法可分为两类:在线模式和批处理模式。在线模式的实时响应性较好，批处理模式调度算法的共性就是在进行调度时以优化任务完成时间为目标。虽然上述算法在解决特定领域问题时具有一定的效果，但还是存有一定的缺陷。尤其是对于高吞吐率应用中的“任务放牧”[12]问题的处理效果不佳，也没有考虑到资源节点的性能度量及任务自身的区别。为此，本文针对高吞吐量应用问题提出了一种新的任务调度算法。

1 基于任务分解的时间均衡调度算法

1．1算法思想

本文提出了一种基于任务分解的时间均衡启发式调度算法(TBSTD，time-balancing heuristic task scheduling algorithm based on task decomposition)。该算法将一个独立任务分解成多个子任务，并使多个分解后的子任务并行执行，任务的完成时间由执行时间最长的子任务决定。显然，当分解后的子任务数目一定时，各子任务在相应调度资源上的完成时间点相同，任务总的完成时间最短。使各个分解后的子任务具有相同的预测完成时间的点的分解策略称为“时间均衡”策略。TBSTD算法是基于时间均衡策略对独立任务进行分解，按具有最小的任务预测完成时间的任务分解方案实施调度，通过使任务分解后的多个子任务并行运行，缩短任务完成时间，提高系统资源的利用率。TBSTD在调度过程中充分考虑到了网格中资源节点具有动态、异构、分布等特点，引入了自动调节因子，并进行重复调度，以使本算法能对任务作出及时响应，能够适应更复杂的实际应用环境。

1．2算法设计与描述

调度问题描述如下：假设网格计算系统中有N个相互独立的任务形成的集合为t={ t[1],t[2],…,t[N] }，M个可用资源形成的集合p={p[1],p[2],…,p[M]}且规定这M个资源的负载低于某一固定阈值，各个可用资源的负载表示为 L[1]，L[2]，…，L[m]。E[k]j表示第k个任务在第j个节点上的预测执行时间, C[k]j表示第k个任务在第j个节点上的预期完成时间。某时刻当用户提交了一个问题规模为w的任务t[k]到达时，t[k]被分解成m个可并行执行的子任务，并定义t[k]分解的子任务为t[k]j, t[k]j的问题规模为wj。为了简化算法的设计，本文算法仅考虑本地任务的调度。

基于任务分解的时间均衡策略实施步骤描述如下：

1)确定任务分解的子任务的期望执行时间；

2)确定时间均衡策略；

3)确定任务的自动调节因子；

4)实施调度。

1．2．1 子任务的期望执行时间

假设本地任务在不同时间内的到达是相互独立的平稳增量过程，子任务t[k]j在资源p[j]上执行期间共有R个任务到达并被执行完成。因为本地任务的到达是平稳过程，所以可认为对充分小的Δt在时间区间[t,t+Δt]内有一个本地任务到达的概率与t无关，而是与区间长Δt成正比;由于在此区间内有两个或两个以上的本地任务到达的概率极小，以至可以忽略不计。又因为在不同时间内的本地任务的到达是相互独立的，所以在wj时间内本地任务的到达数服从泊松分布，为此资源p[j] 对本地任务提供的服务可看作M/G/1排队系统。在M/G/1排队系统中本地任务被资源p[j]处理的平均服务率为μ，平均到达率为λ。μ表示单位时间内能被资源完成的任务数，λ表示单位时间内到达的任务数，ρ表示处理强度，ρ=λ/μ。

本地任务Tk在资源j上的期望完成时间定义为

(1)

由于本地任务的期望完成时间和子任务t[k]j在资源p[j]上执行期间本地任务的到达数R，可建立任务t[k]分解的子任务期望执行时间模型。规模为wj的子任务t[k]j在资源p[j]上的期望执行时间E[k]j可表示为

(2)

其中wj表示子任务的问题规模大小，ρj表示资源p[j]的处理强度，即相同时间内任务平均到达数与被服务的平均数之比。

1．2．2 确定时间均衡策略

在上述1．2．1中确定了子任务的期望执行时间E[k]j由式(2)表示，在此基础上来预测子任务t[k]j预期完成时间。子任务t[k]j在资源j上的预期完成时间等于子任务t[k]j的预期执行时间E[k]j与子任务t[k]j等待资源j提供服务的时间之和，t[k]j等待资源j提供服务的时间是由资源j的负载决定的。当任务分解后的m个任务分别调度到m个相应资源上执行， m个 资源的负载分别表示为L[1]，L[2]，…，L[m]，则子任务t[k]j的预期完成时间表示为

C[k]j=L[j]+E[k]j。

(3)

当任务t[k]分解为m个子任务并行执行时，其完成时间由具有最大完成时间的子任务来决定，即满足：

C[k]m=max{C[k]j}，j=1,2,…，m。

(4)

任务t[k]分解成m个子任务,各个子任务的预期完成时间分别表示为

C[k]1,C[k]2,…，C[k]m,设C[k]1=t1，C[k]2=t2,…，C[k]m=tm,且t1,t2,…,tm不全相等。假设其中t1最大，则任务的预期完成时间C[k]m=1，如果此时任务的预期完成时间最短，则t1与t2,…,tm满足如下关系：ti=t1-Δti，其中i=2,3,…，m。由式(2)和式(3)可知在资源j上执行的子任务t[k]j的问题规模可表示为

wj=(tj-Lj)(1-ρj)，j=1,2,…，m。

(5)

任务t[k]的问题规模w可表示为各个子任务的问题规模之和，即：

(6)

任务完成时间 t1经变换可表示为

(7)

当t1最小时，任务的预期完成时间最短，由式(7)可知当Δtj为零时t1的值最小，即当各个子任务的预期完成时间相同时，任务的预期完成时间最短。与前面假设t1,t2,…,tm不全相等时矛盾，所以仅有当子任务的预期完成时间相等时任务的预期完成时间才最短。

当采用时间均衡进行任务分解时，设分解后的各个子任务的预期完成时间为常数a：

C[k]j=E[k]j+Lj=a。

(8)

由式(6)和式(8)可知，任务t[k]的问题规模w可用下式表示：

(9)

分解后子任务的问题规模wj可重新定义为

wj=(1-ρj)E[k]j。

(10)

由式(8)和式(10)可确定子任务t[k]j的预期执行时间为

(11)

则子任务的预期完成时间为

(12)

由上述可知，当任务分解后的子任务数目确定时，只有各个子任务的预期完成时间全部相等时，才能保证整个任务的预期完成时间最短，即任务分解应采取“时间均衡”策略。任务分解的时间均衡就是解决任务如何在m个资源间进行分解，从而使这种分解模式下任务的预期完成时间最小。

1．2．3 确定任务的自动调节因子

由于计算网格资源自身具有的动态性、异构性、自治性等特点，在进行任务调度时如果采用批处理模式调度算法，会出现“饥饿现象”，饥饿现象是指有些任务长时间得不到调度，这种任务被称为饥饿任务。特别是在使用“等长时间间隔”进行任务调度的系统中经常出现，但在实际的任务调度中这种饥饿现象是不允许出现的。为解决这种饥饿任务的出现，本文引入了自动调节因子。

1．2．4 实施调度

通过上述定义和分析，现给出基于任务分解的时间均衡算法实施调度简要步骤描述如下。

第1步：将当前系统到达的新任务和已经被调度但未被执行的任务收集到任务集t中;

第2步：找到当前系统中现存负载小于固定阈值的M个可用资源，形成可用资源集p;

第3步：依据可用资源当前负载由小到大进行排序;

第4步：将需要进行优先调度的任务附上自动调节因子;

第5步：重新计算任务问题规模并按升序进行排序;

第6步：根据第5步结果，从任务集t中选择任务问题规模最小的任务进行调度;

第7步：取m个资源根据式(12)计算任务的期望完成时间;

第8步：如果C[k]m≤L[m+1]，选择具有最小任务期望完成时间和相应的资源组;

第9步：按式(8)和式(10)实施任务分解并调度到相应资源上执行;

第10步：从任务集中删除执行完毕的任务;

第11步：更新任务集和可用资源信息;

第12步：若任务集t中还有未被调度完成的任务，转到第2步执行，若任务集中的任务都已被调度执行完成，则转到第1步执行。

2 仿真实验与性能分析

针对TBSTD算法，在这里人们使用的是SimGrid[13-15]进行模拟仿真。创建1个中心节点，10个用户节点作为计算资源，任意给出100个相互独立的任务，进行10组仿真实验。在实验中规定任务的计算时间处于0.5～30 s之间。针对相同的任务在仿真平台上对调度事件发生的频率及对算法性能的影响进行了分析。从任务完成总的时间和系统资源利用率方面与Max-min和Max-int算法进行了对比。

图1 γ取不同值时任务完成时间对比图Fig.1 Task completion time while different γ value is used

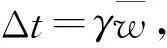
实际上，要使Δt取值最优，γ的取值应是动态变化。从图1中可知当γ=4时系统任务的总的完成时间最小，为此对本算法后面进行的仿真实验中取γ值近似为4。

当取γ=4时分别对100个任务进行了10组实验，从任务完成总的时间和系统吞吐率与Max-min和Max-int算法进行对比，实验结果分别如图2和图3所示。

图2 三种算法完成时间对比图Fig.2 Completion time comparison of three algorithms

图3 三种算法系统吞吐率对比图Fig.3 System throughput rate comparison of three algorithms

由图2可知Max-min算法的任务完成时间为285 s，Max-int算法的任务完成时间为273.7 s， TBSTD算法的任务完成时间为255.5 s,显然相同处理任务情况下TBSTD算法具有较少的任务完成时间。 图3是从3种算法完成相同任务系统吞吐率的方面进行对比，从图3中可知，采用TBSTD算法每秒钟完成的任务的个数多于Max-min和Max-int算法，具有较高的系统吞吐率。从以上实验结果可知，Max-min和Max-int算法进行任务调度时没有对任务进行分解，任务执行的粒度大，不能充分利用空闲可用资源解决问题，从而导致任务总的完成时间较大，系统吞吐率较低。TBSTD算法实施调度时充分考虑了资源的特性，对任务进行分解，分解后的各个子任务可调度到多个可用资源上并行执行，充分利用了系统的空闲资源，从而减少了任务的完成时间，有利于提高系统的吞吐率。

3 结 语

提出的TBSTD调度算法在时间均衡的策略下对任务进行分解，并采用重复调度的方式实施任务调度。通过仿真实验从任务完成时间和系统吞吐率两方面与Max-min和Max-int算法进行对比。实验结果证明本文提出的TBSTD算法在任务总的完成时间和系统吞吐率方面都优于上述两种方法。即本文提出的TBSTD对于“任务放牧”这类问题的调度具有更好的优越性，是一种较好的任务调度算法。

参考文献/References：

[1] CASANOVA H．Network modeling issues for grid application scheduling[J].International Journal of Foundations of Computer Science, 2005，16(2)：145-162.

[2] 丁敏敏．网格计算中改进Min-Min算法的研究[D].西安：西北大学,2010.

DING Minmin.Research of Improved Min-Min Algorithm in Grid Computing[D].Xi′an:Northwest University,2010.

[3] BRAUN T D, JAY S H, NOAH B. A comparison of eleven static heuristics for mapping a class of independent tasks onto heterogeneous distributed computing dystems[J]. Journal of Parallel and Distributed Computing, 2001,61(6)：810-837.

[4] HE Xiaoshan, SUN Xiaohe, LASZEWSKIG V. QoS guided Min-Min heuristic for grid task scheduling[J]. Journal of Computer Science and Technology, 2003, 18(4): 442-451.

[5] YIN Fei, JIANG Changjun,DENG Rong, et al.Gird resource management policies for load-balancing and energy-saving by vacation queuing theory[J].Computer and Electrical Engineering,2009,35(6):966-979.

[6] 彭海云,李 骞,李 强.网格环境下资源负载均衡和优化调度研究[J].计算机工程与应用,2009,45(19):104-106.

PENG Haiyun, LI Qian,LI Qiang. Research on resources load balancing and task scheduling optimal algorithm in grid environment [J].Computer Engineering and Applications, 2009,45(19):104-106.

[7] 于 策，孙济洲,李明楚，等.一种应用于网格计算环境的任务调度模式[J].计算机应用研究, 2008,25(5):1500-1503.

YU Ce, SUN Jizhou,LI Mingchu,et al.Task scheduling pattern for grid computing environment[J].Application Research of Computers, 2008,25(5):1500-1503.

[8] 李玲娟,史祥宁,王汝传.一种基于改进蚂蚁算法的网格任务调度策略[J].南京邮电大学学报(自然科学版),2008,28(3):17-20.

LI Lingjuan， SHI Xiangning, WANG Ruchuan. An improved ant algorithm-based task scheduling strategy in grid[J]. Journal of Nanjing Unicersity of Posts and Elecommunications (Natural Science), 2008,28(3):17-20.

[9] 孟宪福, 闫玲玲,刘伟伟. 基于动态任务优先级的网格任务调度算法研究[J].大连理工大学学报, 2012，52(2):277-281.

MENG Xianfu, YAN Lingling,LIU Weiwei. Research on task scheduling algorithm in grid computing systems based on dynamic task priority[J].Journal of Dalian University of Technology, 2012，52(2):277-281.

[10] 刘波涛，刘金广.基于动态粒子群优化的网格任务调度算法[J].计算机应用研究,2011，28(3):938-940.

LIU Botao, LIU Jinguang. Novel scheduling algorithm based on dynamic particle swarm optimization[J].Application Research of Computers, 2011，28(3):938-940.

[11] 林剑柠,吴慧中.一种基于动态决策路径的网格任务调度算法[J].计算机研究与发展, 2008,45(5): 841-847.

LIN Jianning, WU Huizhong.A new scheduling algorithm in grid based on dynamic decisive path[J]. Journal of Computer Research and Development, 2008,45(5): 841-847.

[12] 胡艳丽,张维明,肖卫东，等. 计算网格中基于时间均衡的并行粗粒度任务调度算法[J]. 小型微型计算机系统,2008(1):124-129.

HU Yanli,ZHANG Weiming,XIAO Weidong, et al.A dynamic scheduling algorithm of parallel coarse grain tasks in computational grid based on time-balancing strategy[J]. Journal of Chinese Computer Systems, 2008(1):124-129.

[13] 金 海，袁平鹏，石 柯.网格计算[M].北京:电子工业出版社，2004.

JIN Hai,YUAN Pingpeng,SHI Ke.Gird Computing[M].Beijing:Pbulishing House of Electronics Industry,2004.

[14] 罗 红,慕德俊,邓智群,等. 网格计算中任务调度研究综述[J].计算机应用研究, 2005,22(5)：16-19.

LUO Hong, MU Dejun, DENG Zhiqun, et al.A review of job scheduling for grid[J].Application Research of Computers, 2005,22(5)：16-19.

[15] 查 礼，徐志伟，林国璋，等.基于Simgrid 的网格任务调度模拟[J].计算机工程与应用，2003(14)：90-92.

ZHA Li,XU Zhiwei,LIN Guozhang,et al.Grid task scheduling simulations based on Simgrid[J].Computer Engineering and Applications, 2003(14)：90-92.

[16] 张京军，刘文娟，刘光远.基于改进免疫遗传算法的网格任务调度[J].河北工程大学学报(自然科学版)，2013，30(2)：80-83.

ZHANG Jinjun,LIU Wenjuan, LIU Guangyuan.Task scheduling in grid computing based on improved immune genetic algorithm[J].Journal of Hebei University of Engineering(Natural Science Edition),2013,30(2):80-83.