基于MATLAB的切比雪夫II型数字低通滤波器设计

王艳文 史先红

(1.新乡医学院 生命科学技术学院，河南 新乡 453003；2.许昌学院 公共实验中心,河南 许昌 461000)

干扰抑制常见的模拟滤波器是巴特沃斯(Butterworth)滤波器和切比雪夫(Chebyshev)滤波器。巴特沃斯滤波器的特点是具有通带内最大平坦的振幅特性，且随频率，升高，幅频特性单调递减。切比雪夫滤波器在通带范围内是等幅起伏的，所以同样的通带衰减，其阶数较巴特沃斯滤波器要小。可根据需要对通带内允许的衰减量(波动范围)提出要求，如要求波动范围小于1dB[1,2]。

MATLAB是美国MathWorks公司推出的一套用于工程计算的可视化高性能语言与软件环境，是数字信号处理技术实现的重要手段[3]。本文采用脉冲响应不变法实现Chebyshev数字滤波器的设计。

1 程序设计及运行结果

根据研究任务，利用切比雪夫模拟滤波器，通过脉冲响应不变法设计切比雪夫II型数字低通滤波器。数字滤波器的技术指标为，0.90≤≤1，0≤≤0.25π，≤0.18，0.35π≤≤π，采样周期为T=2。

设计程序如下：

T=2; %设置采样周期为2

fs=1/T; %采样频率为周期倒数

Wp=0.25*pi/T;

Ws=0.35*pi/T; %设置归一化通带和阻带截止频率

Ap=20*log10(1/0.9);

As=20*log10(1/0.18); %设置通带最大和最小衰减

[N,Wc]=cheb2ord(Wp,Ws,Ap,As);%调用cheb2ord函数确定切比雪夫II型滤波器阶数

[B,A]=cheby2(N,Ap,Wc); %调用cheby2函数设计切比雪夫II型滤波器

W=linspace(0,pi,400*pi); %指定一段频率值

hf=freqs(B,A,W); %计算模拟滤波器的幅频响应

subplot(2,1,1);

plot(W/pi,abs(hf)/abs(hf(1)));%绘出切比雪夫II型模拟滤波器的幅频特性曲线

grid on;

title('切比雪夫II型模拟滤波器');

xlabel('Frequency/Hz');

ylabel('Magnitude');

[D,C]=impinvar(B,A,fs); %调用脉冲响应不变法

Hz=freqz(D,C,W); %返回频率响应

subplot(2,1,2);

plot(W/pi,abs(Hz)/abs(Hz(1)));%绘出切比雪夫II型数字低通滤波器的幅频特性曲线

grid on;

title('切比雪夫II型数字滤波器');

xlabel('Frequency/Hz');

ylabel('Magnitude');

2 结果分析

运行程序，可得滤波器阶数为N=3，Wc=0.5498。符合设计要求。切比雪夫II型数字低通滤波器的幅频特性曲线如图1所示。

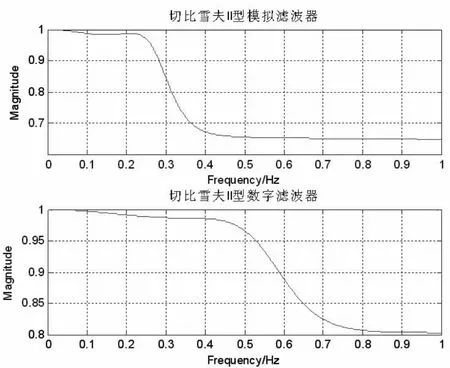
图1 切比雪夫II型数字低通滤波器的幅频特性曲线

3 结语

利用MATLAB设计滤波器方法简单、快捷直观。本文运用脉冲响应不变法，利用切比雪夫模拟滤波器设计了切比雪夫II型数字低通滤波器，程序运行结果符合设计技术指标要求，取得了较理想的实验效果。

［1］李勇.MATLAB辅助现代工程数字信号处理[M].西安:西安电子科技大学出版社，2002:83-95.

［2］董霖.MATLAB 使用详解[M].北京:科学出版社，2008:507-513.

［3］石云霞.MATLAB在滤波器设计中的应用[J].青岛建筑工程学院学报，2004，25(2)：93-96.