关于Diophantine方程x3±1＝3 Dy2

杜先存，吴丛博，赵金娥

（1.红河学院a.教师教育学院，b.数学系，云南 蒙自 661199；2.北京理工大学 理学院，北京 100081）

方程x3±1＝Dy2（D 是无平方因子的正整数）是一类重要的Diophantine方程，其整数解已有不少人研究过.柯召、孙琦［1］证明了当D 不含6k＋1型的素因子时，方程x3±1＝3Dy2无整数解，但当D 含6k＋1型的素因子时，方程的求解较为困难.韩云娜［2］得出了方程x3±1＝3py2无正整数解的一个充分条件.陈晓化、李志苹［3］得出了方程x3＋1＝3py2无正整数解的一个充分条件.乐茂华［4］得出了方程x3＋1＝3py2无正整数解的一个充分条件.乐茂华［5］得出了方程x3-1＝3py2无正整数解的一个充分条件.杜先存等［6］给出了方程x3-1＝Dy2无正整数解的一些充分条件.杜先存等［7］给出了方程x3-1＝py2无正整数解的三个充分条件.

1 引 理

引理［8］设a＞1，（a，b）∈N2，ab 不是完全平方数，若ax2-by2＝1有解（x，y）∈N2，设是方程ax2-by2＝1（x，y∈Z）的基本解，则ax2-by2＝1的任一组解可以表示为

2 主要结论

2.1 定理1及证明

定理1 设D＝27t2＋1（t∈Z＋）为奇素数，则Diophantine方程

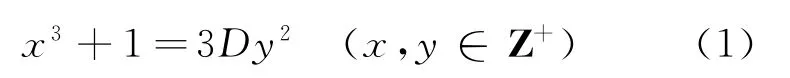
无正整数解.

证明 设（x，y）是方程（1）的正整数解，由费马小定理可知x3≡x（mod3），故有x3＋1≡x＋1≡0（mod3），此时x2-x＋1≡0（mod3），故gcd（x＋1，x2-x＋1）＝3.又因为x＋1≡0（mod3），则有x2-x＋1≢0（mod9）.故方程（1）可分解为以下两种情形.

情形Ⅰ x＋1＝9Du2，x2-x＋1＝3v2，y＝3uv，gcd（u，v）＝1；

情形Ⅱ x＋1＝9u2，x2-x＋1＝3Dv2，y＝3uv，gcd（u，v）＝1.

对于情形Ⅰ，将第一式代入第二式，得（18Du2-3）2＋3＝3（2v）2，即

因此，式（2）的全部整数解可表示为

式中，（2，1）是Pell方程x2-3y2＝1的基本解，因此有6Du2-1＝±yn（n∈Z），即6Du2＝±yn＋1.又因为y-n＝-yn，所以只需考虑

由式（3）得，yn≡-1（mod6）.容易验证下列各式成立：

对递归数列（4）取模6，其剩余类周期为6，当n ≡-1（mod6）时，有yn≡-1（mod6）.故只有当n ≡-1（mod6）时式（4）才成立.

对递归数列（4）取模8，其剩余类周期为4，当n ≡1（mod4）时，有yn≡1（mod8）.由式（3）得，6Du2＝yn＋1≡2（mod8），则 有3Du2≡1（mod4）.因为D＝27t2＋1（t∈Z＋），所以D ≡3t2＋1≡0，1（mod4），又因为D为奇素数，所以D ≡1（mod4）.又因为u2≡0，1（mod4），所以3Du2≡0，3（mod4），这与“3Du2≡1（mod4）”矛盾，故只有当n ≡-1（mod4）时式（3）才成立.

综上，当n ≡-1（mod12）时式（3）才成立.

当n ≡-1（mod12）时，若n≠-1，设n＝3r·t-1，式中，r≥1，t ≡±4（mod12），则由式（3）、式（4）、式（5），得，即6Du2≡-208≡2（mod15），则有3Du2≡1（mod15），从而有3Du2≡1（mod3），矛盾.

若n＝-1，由式（3）得6Du2＝y-1＋1＝0，则有u＝0，从而给出方程（1）的平凡解为（x，y）＝（-1，0）.

所以情形Ⅰ无方程（1）的正整数解.

对于情形Ⅱ，将第一式代入第二式，整理，得

则（2v，6u2-1）是方程（1）的一组解.因为D＝27t2＋1（t∈Z＋），所以（1，3t）是方程Dx2-3y2＝1的最小解.

由引理，式（6）可表示为

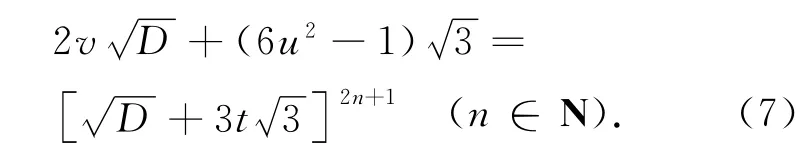
由式（7）可得6u2-1≡0（mod3t），故6u2-1≡0（mod3），因此，6u2≡1（mod3），这不可能.由此可知，情形Ⅱ不成立.

综上，当D＝27t2＋1（t∈Z＋）为奇素数时，方程（1）无正整数解.

2.2 定理2及证明

定理2 设D＝27t2＋1（t∈Z＋）为奇素数，则Diophantine方程

无正整数解.

证明 设（x，y）是方程（8）的正整数解，由费马小定理可知x3≡x（mod3），故有x3-1≡x-1≡0（mod3），此时x2＋x＋1≡0（mod3），故gcd（x-1，x2＋x＋1）＝3.又因为x-1≡0（mod3），则有x2＋x＋1≢0（mod9），故式（8）可分解为以下两种情形.

情形Ⅲ x-1＝9Du2，x2＋x＋1＝3v2，y＝3uv，gcd（u，v）＝1；

情形Ⅳ x-1＝9u2，x2＋x＋1＝3Dv2，y＝3uv，gcd（u，v）＝1.

对于情形Ⅲ，将第一式代入第二式，得（18Du2＋3）2＋3＝3（2v）2，即

因此，式（9）的全部整数解可表示为

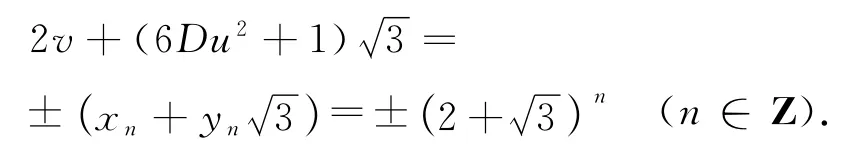
式中，（2，1）是Pell方程x2-3y2＝1的基本解，因此有6Du2＋1＝±yn（n∈Z），即6Du2＝±yn-1.又因为y-n＝-yn，所以只需考虑

由式（10）得，yn≡1（mod6）.

对递归数列（4）取模6，其剩余类周期为6，当n ≡1（mod6）时，有yn≡1（mod6）.故只有当n ≡1（mod6）时式（10）才成立.

当n ≡1（mod6）时，若n≠1，设n＝3×2r·t＋1，式中，r≥1，t ≢0（mod2），则由式（3）、式（4）、式（10），得6Du2＝y2×3（2r-1×t-1）＋7-1≡±y7-1（mody3）.则当r＞1时，有6Du2≡-y7-1（mody3），即6Du2≡-2 912≡-2（mod15），则有3Du2≡-1（mod15），从而有3Du2≡-1（mod3），矛盾.从而r＝1，此时n ≡7（mod12）.故只有当n ≡7（mod12）时式（10）才成立.

当n ≡7（mod12）时，若n ≠7，设n＝3s·m＋7，式中，s ≥1，m ≡±4（mod12），则由式（3）、式（4）及式（10），得），即6Du2≡-2（mod15），则有3Du2≡-1（mod15），从 而 有3Du2≡-1（mod3），矛盾.

当n＝1时，由式（10）得6Du2＝y1-1＝0，则有u＝0，从而给出式（9）的平凡解为（x，y）＝（1，0）.

当n＝7 时，由 式（10）得6Du2＝y7-1＝2 910，即Du2＝485，显然不成立.

所以情形Ⅲ无方程（9）的正整数解.

对于情形Ⅳ，将第一式代入第二式，整理，得

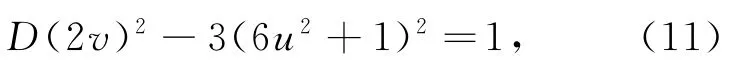
则（2v，6u2＋1）是方程（1）的一组解.因为D＝27t2＋1（t∈Z＋），所以（1，3t）是方程Dx2-3y2＝1的最小解.

由引理，式（11）可表示为

由式（12）可得6u2＋1≡0（mod3t），故6u2＋1≡0（mod3），因此6u2≡2（mod3），这不可能.由此可知，情形Ⅳ不成立.

综上，当D＝27t2＋1（t∈Z＋）为奇素数时，方程（8）无正整数解.

3 结 语

本文通过对D＝27t2＋1（t ∈Z＋）时Diophantine方程x3±1＝3Dy2的解的存在性的讨论，得出了Diophantine方程x3±1＝3Dy2无正整数解的一个充分条件.

［1］柯召，孙琦.关于丢番图方程x3±1＝3 Dy2［J］.四川大学学报：自然科学版，1981，18（2）：1-5.（Ke Zhao，Sun Qi.On the Diophantine Equation x3±1＝3 Dy2［J］.Journal of Sichuan University：Natural Science，1981，18（2）：1-5.）

［2］韩云娜.关于Diophantine方程x3±1＝3py2［J］.高师理科学刊，2010，30（3）：41-42.（Han Yunna.On the Diophantine Equation x3±1＝3py2［J］.Journal of Science of Teachers' College and University，2010，30（3）：41-42.）

［3］陈晓化，李志苹.关于Diophantine方程x3＋1＝3py2［J］.重庆工学院学报：自然科学版，2009，23（4）：44-45.（Chen Xiaohua，Li Zhiping.On the Diophantine Equation x3＋1＝3py2［J］.Journal of Chongqing Institute of Technology：Natural Science，2009，23（4）：44-45.）

［4］乐茂华.关于Diophantine方程x3＋1＝3py2［J］.保定师范专科学校学报，2004，17（2）：12-13.（Le Maohua.On the Diophantine Equation x3＋1＝3py2［J］.Journal of Baoding Teachers'College，2004，17（2）：12-13.）

［5］乐茂华.关于Diophantine方程x3-1＝3py2［J］.广西师范学院学报，2005，22（4）：22-23.（Le Maohua.On the Diophantine Equation x3-1＝3py2［J］.Journal of Guangxi Teachers Education University，2005，22（4）：22-23.）

［6］杜先存，李玉龙，赵金娥.关于不定方程x3-1＝Dy2［J］.四川理工学院学报：自然科学版，2012，25（4）：79-80.（Du Xiancun，Li Yulong，Zhao Jin'e.Indefinite Equation x3-1＝Dy2［J］.Journal of Sichuan University of Science ＆Engineering：Natural Science，2012，25（4）：79-80.）

［7］杜先存，史家银，赵金娥.关于不定方程x3-1＝py2［J］.西南民族大学学报：自然科学版，2012，38（5）：748-751.（Du Xiancun，Shi Jiayin，Zhao Jin'e.On the Indefinite Equation x3-1＝py2［J］.Journal of Southwest University for Nationalities：Natural Science，2012，38（5）：748-751.）

［8］夏圣亭.不定方程浅说［M］.天津：天津人民出版社，1980：97-98.（Xia Shengting.Elementary Introduction to Indeterminate Equation［M］.Tianjin：Tianjin People's Publishing House，1980：97-98.）