关于混合ARMA（1,1）过程的研究

杨明洁 訾雪旻 段美华

（天津职业技术师范大学 理学院，中国 天津 300222）

0 引言

时间序列是根据时间顺序得到的一系列观测值，它的典型特征是相邻观测值之间存在一定的依赖性。许多理论或实际生活中的数据就是以这种时间序列的形式呈现的。

1 一阶自回归——一阶移动平均模型ARMA(1,1)[1]

对于自相关过程，如果在t时刻的过程值zt，不仅与过程先前值有关，而且与先前时刻的随机扰动也存在一定的关系时，就应用自回归——移动平均混合模型来模拟自相关数据，混合模型为：

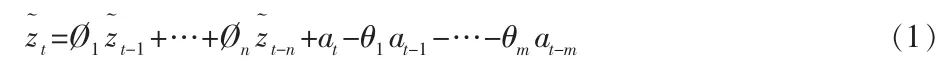
不失一般性，本文将应用一阶自回归——一阶移动平均过程，即混合ARMA(1,1)过程来描述自相关的观测值，并假设均值μ=0，模型为：

2 控制图的应用

应用EWMA、REWMA、T2和RT2四个控制图来监测混合 ARMA(1,1)模型，这些控制图在很多论文及相关书籍中都有介绍，在这里就不加以赘述。

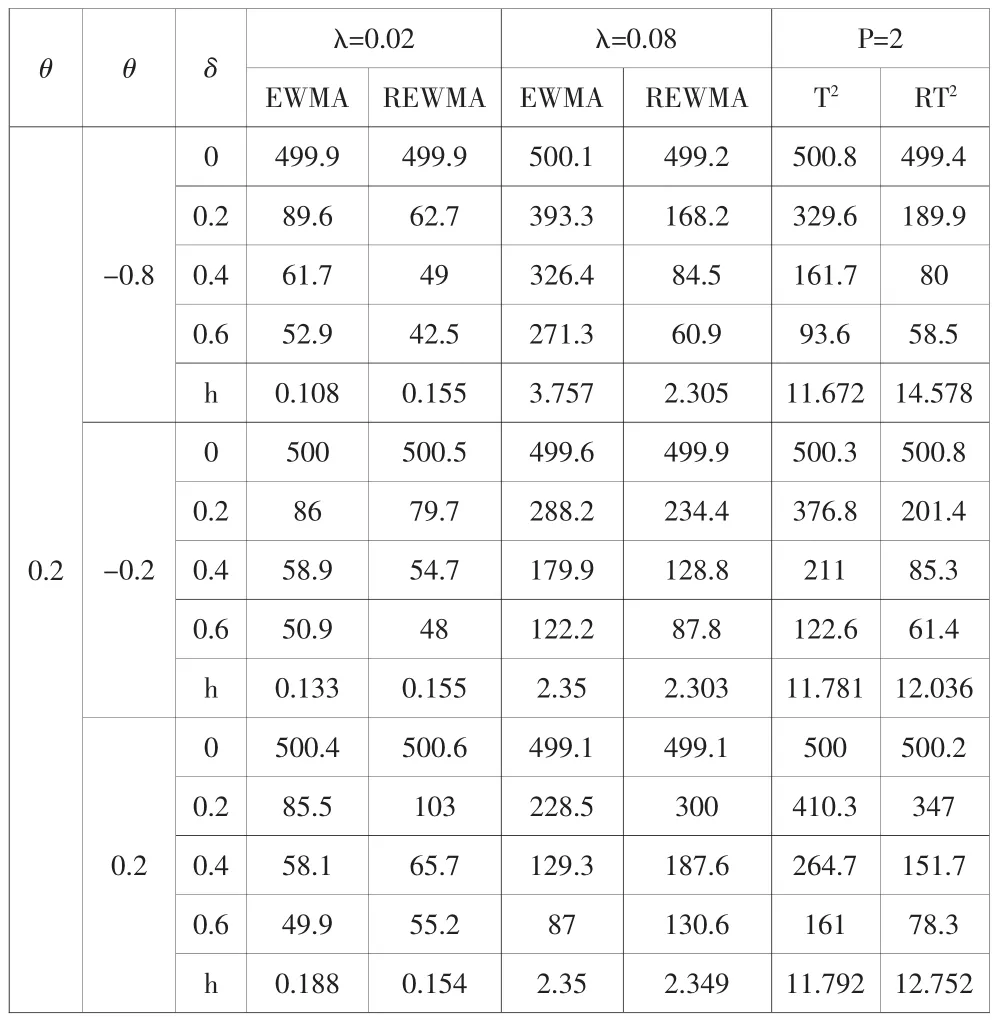
表1 EWMA、REWMA、T2和RT2控制图在θ=0.2时的ARL对比值

Apley和Tsung(2002)[2]详细给出了如何选择最优窗宽以及如何规定第一类错误概率α的方法，此处不再赘述。在本文中选择的最佳移动窗宽为p=2，第一类错误概率为α=0.002。λ为EWMA和REWMA的光滑系数。以0＜θ＜1为代表，下表表1、表2分别给出EWMA、REWMA、、T2和RT2控制图在 θ=0.2和θ=0.8时的ARL值。

结果显示，在 λ 极小（0.02）且 Ø=-0.2、δ=0.2 时，79.7<86.0<201.4<376.8（分别为 EWMA、REWMA、、T2和 RT2的 ARL 值），因此在此时最优的为REWMA控制图。同理，我们可以得到规律见表3。

当 λ 极大（0.8）且 Ø=-0.8、δ=0.2 时，173.2<191.8<350.1<421.5（分别为RT2、REWMA、T2和EWMA的 ARL值），因此在此时最优的为RT2控制图。同理，我们也可以得到规律见表3。

表3 当0＜θ＜1时，监测中小漂移的最优控制图的选择

表4 当-1＜θ＜0时，监测中小漂移的最优控制图的选择

应用同样的方法，可以得到当-1＜θ＜0时的控制图的选择情况，见表4

3 结果分析

结果表明，对于混合 ARMA(1，1)模型来说，当 0＜θ＜1 时，从整体来看，残差控制图要比原控制图相对有优势，当光滑系数λ极小时，可以选择使用REWMA控制图；当λ极大时，可以考虑应用RT2控制图；当-1＜θ＜0 且－1＜Ø＜0 时，残差控制图要占主导，当－1＜Ø＜-0.5（不考虑λ的影响）和-0.5＜Ø＜0且λ极小时，可以考虑使用REWMA控制图；当-0.5＜Ø＜0 且 λ 极大时，应用 RT2控制图；当-1＜θ＜00＜Ø＜1 且时，应用EWMA控制图为最优。

[1]乔治 E.P.博克斯.时间序列分析[M].机械工业出版社,2002.

[2]王兆军,邹长亮,李忠华.统计质量控制图理论与方法[M].科学出版社,2013.