一种进场着陆阶段的模型跟踪控制律设计
张喆, 祁圣君, 王锋
(中国飞行试验研究院 飞机所, 陕西 西安 710089)
一种进场着陆阶段的模型跟踪控制律设计
张喆, 祁圣君, 王锋
(中国飞行试验研究院 飞机所, 陕西 西安 710089)
为进行进场着陆阶段飞机俯仰角速度、航迹、迎角等参数的空中飞行模拟,根据模型相似准则,以经典控制原理进行升降舵控制、直接升力控制和自动油门控制的纵向模型跟踪控制律设计,并在Simlink环境下进行数值仿真。仿真结果表明,所设计的控制律可以满足跟踪模拟的要求。
变稳飞机; 空中飞行模拟; 经典控制理论; 模型跟踪
0 引言
对于电传飞机飞控系统控制律设计而言,进场着陆控制律设计是最具挑战性的任务[1-2]。国外电传飞机试飞中,着陆过程发生过多次由飞控系统引起的事故,如JA-S39和YF-22在着陆过程中,由于控制律设计缺陷发生坠机事故;因此国外极其重视起降阶段控制律的空中飞行模拟研究。JAS-39坠机事件后,Calspan公司利用NT-33和LEARJET变稳飞机验证其控制律并进行改进,完善了该机的控制律设计。“九五”期间,我国利用K-8飞机为原型机建成了IFSTA变稳飞机进行控制律验证试验[3]。该机为三轴变稳飞机,其控制操纵面包括副翼、方向舵、升降舵,利用该机可以模拟模型对象绕三轴的角运动。但由于缺少纵向和法向力控制,该机无法实现航迹等特性的模拟,而这些对于一些特殊的进场任务模拟来说是非常必要的[4]。
本文根据线性模型跟踪的理论和设计思想,采用文献[5]提出的同时具备自动油门控制、直接升力控制和升降舵控制的纵向动力学模型,进行综合模型跟踪控制律设计。
1 模型跟踪控制律设计
1.1 动力学模型
采用TIFS飞机纵向动力学模型[2]作为平台进行控制律设计,其状态空间形式为:
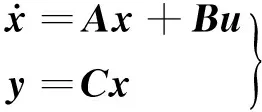
(1)
其中:
x=[ΔVΔαΔqΔθ]T
u=[δeδLδT]T
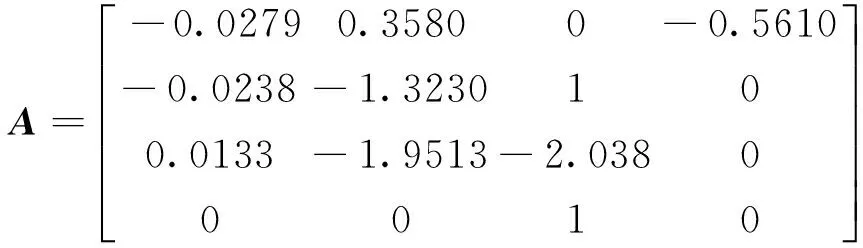

式中,δe为升降舵;δL为直接升力舵面;δT为自动油门位置;C为选择输出矩阵。
模型对象选择某型当代典型的电传飞机,选取的模拟状态点为H=1 000 m,Ma=0.3。首先进行内回路设计,然后将模型对象进行等效拟配,得到的模态参数即可作为内回路期望配置的特征结构进行设计[6-7]。
1.2 模型对象的等效拟配
现代电传飞机的飞控系统是一个复杂的高阶系统,通常将纵向或横向的高阶飞机等效为具有特定形式的低阶等效飞机,然后再利用低阶等效系统按照军用规范进行飞行品质评估。
目标模型纵向等效拟配的等效二阶模型为:

(2)
从式(2)可以看出,该模型的增益为-0.6695,1/Tθ2为1/1.0805 s,时间延迟项为0.0346s,阻尼比为0.6887,短周期频率为1.9002 rad/s。
1.3 内回路参数设计
内回路设计的目的是匹配模型的短周期频率ωsp,阻尼比ζsp,ny/α以及长周期频率ωp。由迎角和俯仰角速度到升降舵的反馈匹配模型对象的频率和阻尼比;由迎角到直接升力面的反馈匹配ny/α;由速度到油门杆的反馈匹配长周期频率。由迎角至升降舵的反馈KαLz改变短周期频率;由俯仰角速度至升降舵反馈Kqzc改变短周期阻尼比;由驾驶杆指令增益KFz调整短周期响应幅值大小。内回路原理框图如图1所示。

图1 内回路原理框图Fig.1 Principle frame of inner loop
增益参数计算时,采用系数对比法可确定KFz=0.0940,Kqzc=-0.1391,KαLz=-0.0195。将此组增益代入Simlink中进行仿真计算,并对参数进行微调,最终确立的补偿回路参数为:KFz=0.0940,Kqzc=-0.18,KαLz=-0.1。

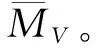
长周期传递函数频率和阻尼比可表达为:
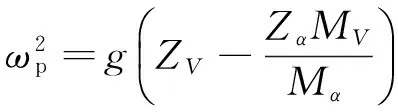
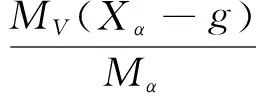

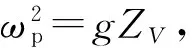

1.4 跟踪回路设计
外回路跟踪环设计是在内回路参数已确定的条件下,根据系统的跟踪精度和跟踪性能而进行参数设计。当仅引入模型与原型机状态误差进行反馈时,在阶跃输入下会引起稳态误差,所以此时引入积分项消除稳态误差。对于理想的跟踪环,希望系统呈现出高频大阻尼的特性,必要时可引入微分项,从而使跟踪回路构成PID跟踪环。通过加入跟踪环,可以取得理想的跟踪效果。原型飞机与模型飞机的纵向短周期特性如表1所示。
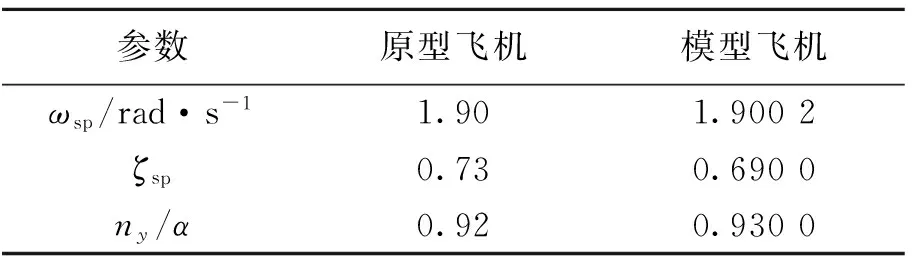
表1 纵向短周期特性Table 1 Longitudinal short period characteristic
2 仿真结果及分析
本文的控制律仿真试验在飞行仿真室的通用变稳地面试验台上进行,该地面试验仿真平台主要包括:座舱操纵系统、视景系统、计算机/网路系统和控制台系统。试验任务为进场着陆模拟,在场高100 m时,进行纠偏着陆,对准另一条跑道完成进场。仿真结果如图2所示,图中给出了在下降过程中进行纠偏时的跟踪效果,其中迎角为基于平衡状态的迎角增量。由于此过程中速度变化仅为5 km/h,所以图中未显示速度的跟踪效果。
从仿真结果可以看出,该控制律具有良好的跟踪效果,跟踪误差在5%以内。同时,利用经典控制理论设计的横航向控制律也满足跟踪要求。

图2 跟踪效果图Fig.2 Tracking effect
3 结束语
本文采用经典控制理论、基于线性小扰动模型设计了进场着陆段的模型跟踪控制律,通过仿真试验验证了该控制律具有良好的跟踪效果。对于多自由度的空中飞行模拟任务,通过对控制律的精心设计,可以在满足跟踪精度的同时,使系统具有良好的闭环稳定性。该工作为下阶段建设五自由度变稳飞机提供了一套有效的设计方法。
[1] 周自全,张子彦.飞行品质和飞行安全[J].飞行力学,2009,27(2):1-6.
[2] 周自全,赵永杰.空中飞行模拟与电传飞机飞行试验[J].飞行力学,2005,23(2):19-22
[3] 刘兴堂,吕杰,周自全.空中飞行模拟器[M].北京:航空工业出版社,2003:185-186.
[4] 汤连刚,李存宝.变稳飞机和飞行品质试飞的体会和评述[J].飞行力学,1989,7(4):87-91.
[5] Nield IV G C.A model-following technique for insensitive aircraft control systems[R].ADA-106742,1963.
[6] Motyka P R.The theory and flight verification of the model-following control system for the air force total in-flight simulator[R].AIAA-71-961,1971.
[7] Motyka P R.A classical approach to the design of model-following control systems[R].AIAA-74-0913,1974.
[8] 徐鑫福,冯亚昌.飞机飞行操纵系统[M].北京:北京航空航天大学出版社,1989:99-100.
Designofmodel-followingcontrollawforapproachandlanding
ZHANG Zhe, QI Sheng-jun, WANG Feng
(Aircraft Flight Test Technology Institute, CFTE, Xi’an 710089, China)
In-flight simulation in the stage of approach and landing focuses on the simulation of some important parameters, such as angle of attack, flight-path angle, pitch rate and so on. According to the similarity criterion, longitudinal control law includes the control of elevator, direct lift and automatic throttle. This paper describes the design of model-following control law in terms of classical control theory. Digital simulation results by Simlink show that the control law could meet the requirements of model-following, which is a feasible attempt for control law design of variable stability aircraft.
variable stability aircraft; in-flight simulation; classical control theory; model-following
V212.1; V249.1
A
1002-0853(2013)05-0447-03
2012-12-27;
2013-06-04; < class="emphasis_bold">网络出版时间
时间:2013-08-21 16:15
张喆(1985-),男,陕西扶风人,助理工程师,硕士研究生,主要从事飞行力学、飞行控制等方面研究。
(编辑:李怡)

