面向控制的飞行器气动耦合模型解耦方法研究

朱多宾, 呼卫军, 林鹏, 周军

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

面向控制的飞行器气动耦合模型解耦方法研究

朱多宾, 呼卫军, 林鹏, 周军

(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)

针对气动交联耦合所带来的飞行器控制系统设计复杂、控制性能无法采用现有的控制系统评价方法等设计问题,提出了一种新的气动耦合模型解耦方法。该方法引入了气动耦合评价指标——气动耦合度,建立了气动弱耦合与气动强耦合的耦合度区间,提出了耦合忽略与等效转换两种解耦方法;实现了飞行器各通道气动耦合条件下模型的完全或部分解耦,利于采用工程中常用的SISO控制系统设计与评价方法。仿真结果表明了面向控制的气动耦合模型解耦方法的有效性。

气动耦合; 气动耦合度; 面向控制解耦

0 引言

高超声速飞行器具有响应快、机动能力强等特点,已成为未来军事斗争新的“制高点”,各国掀起了研究和发展高超声速飞行器的热潮[1]。但其面对称、翼身融合等气动布局方式使得通道间气动交联耦合作用明显,给控制系统设计带来了困难[2]。

针对多变量系统交联影响问题,通常采用解耦的方法实现一个输入只控制一个输出。目前,公开文献的解耦思路主要有两种:一种是基于反馈线性化思想实现通道间解耦[3-4],如动态逆解耦,它是一种精确解耦方法,但需要在整个飞行包线内对飞行器非线性模型进行实时解析求逆,所设计的系统鲁棒性较差,且设计过程复杂;另一种是基于系统辨识方法的简化耦合模型[5-6],对模型无特殊要求,缺点是需要辨识的参数多、计算量大,不利于方案设计阶段快速分析对象的耦合特性。而工程中普遍采用的仍是传统的三通道独立设计法,其基本思路是:首先忽略全部耦合因素,将飞行器耦合通道人为“解耦”;然后对各通道独立设计控制器,保留一定稳定裕度;最后再引入被忽略的耦合关系,通过仿真对设计进行校验。缺点是需要多次尝试才能确定控制器的参数,具有一定的盲目性和不确定性[7]。

本文针对上述方法存在的问题,基于单变量控制系统相对多变量系统理论更加成熟、分析和评价方法更贴近工程实际应用等特点,研究面向控制的气动耦合模型解耦方法。以俯仰通道为例,定义飞行器气动耦合评价指标气动强/弱耦合,提出气动耦合解耦条件和解耦方法。

1 气动力矩耦合模型

本文采用气动导数形式描述运动参数对气动力矩的影响。在所研究特征点附近,气动力矩在三通道分量以气动角、滚转角速度和舵偏角的线性函数表示为:

(1)

在不同气动外形和弹道包线特点下,飞行器气动耦合特性不同[8-9]。文献[10-11]分别研究了GHV和X-43外形下气动特性,其耦合项组成也不尽相同。式(1)考虑了飞行器所有可能的气动耦合项,而具体飞行器实际模型中耦合项的有无与强弱,需经过工程估算和CFD计算予以验证。

按照气动耦合产生的机理将通道间气动耦合效应分为三类:稳定力矩耦合、操纵力矩耦合和阻尼力矩耦合。将式(1)中各气动耦合项分类整理如表1所示。

表1 三通道气动耦合项分类Table 1 Classification of 3-channel aerodynamic coupling item

由多变量控制理论[12-13],将建立的气动耦合模型描述为:

(2)

式中,Mi为气动力矩在i通道的分量;Aij(3×3)为i通道相对j通道的系数矩阵;Ri(3×1)为i通道中对应的气动角、滚转角速度和舵偏。

式(2)的气动力矩模型为标称模型,考虑到不确定性因素的影响,实际对象的系数矩阵表示为标称模型与不确定性因素的和[14]:

(3)

式中,Δ描述了模型参数大范围或小范围的有界不确定性,或随机时变和摄动的不确定性。

2 气动耦合评价指标

2.1 气动耦合评价指标定义

矩阵A为非对角分块矩阵,描述了各通道间耦合作用。若Aij≠0(i≠j),各通道间存在耦合,可能使系统的稳定裕度下降。若通道间的系数矩阵A满足

A=diag[A11,A22,…,Aij]

(4)

则A为分块对角矩阵,各通道不存在耦合。

以上仅为定性描述,定量描述系统耦合强弱在数学上不容易做到,需要工程实践经验。多变量控制理论以系数矩阵对角优势度定量描述耦合的大小[12]。本文基于以下两点对传统对角优势度定义进行了扩充,实现对气动耦合特性的合理描述:

(1)不同类别气动耦合有各自对角优势度定义;

(2)优势度大小不仅与系数矩阵A有关,还应与输入量或状态量的模大小有关。

扩充后对角优势度定义如下:

(5)

2.2 稳定力矩耦合度

稳定力矩耦合项表示其他通道气动角所引起的气动力矩项,俯仰通道稳定力矩耦合度为:

(6)

式中,z为俯仰通道;η为气动角引起的稳定耦合力矩项。

2.3 操纵力矩耦合度

操纵力矩耦合项是其他通道操纵舵面偏转所引起的气动力矩项,俯仰通道操纵力矩耦合度为:

(7)

式中,z为俯仰通道;δ为舵面偏转引起的操纵力矩耦合项。

2.4 阻尼力矩耦合度

阻尼力矩耦合项是绕其他通道轴所引起的气动力矩项,俯仰通道阻尼力矩耦合度如下:

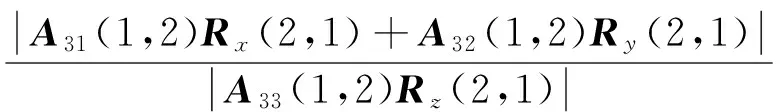
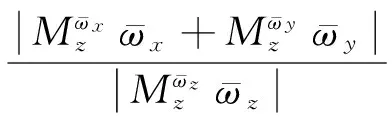
(8)

式中,z为俯仰通道;ω为导弹绕轴转动的阻尼力矩耦合项。

3 耦合度区间划分及强/弱耦合定义

以稳定力矩耦合为例,基于气动耦合度大小,划分强/弱耦合对应的耦合度区间。

3.1 气动弱耦合定义

如前所述,通道间气动交联耦合程度用耦合度定量描述,故可以通过气动耦合度区间定义气动强/弱耦合。以俯仰通道为例,定义稳定力矩弱耦合为稳定力矩耦合度不高于kb,即

(9)

对于不同飞行器,由于其对象特性和飞行弹道包线特点的不同,其弱耦合的上界kb随之不同,可以通过飞行器开环特性分析确定。

3.2 气动强耦合定义

当气动耦合度超过弱耦合上界时,通道间气动交联耦合效应变得明显,定义气动强耦合的下界为kb。随着气动耦合度不断增大,通道间的耦合越来越严重,当耦合超出控制系统能力时,将无法实现气动解耦。故飞行器控制能力决定着气动强耦合的上界值。

稳定力矩和稳定耦合力矩共同作用下,当偏转该通道气动舵面后可控制飞行器达到指令姿态,则飞行器可控,否则不可控。以飞行器各通道可控临界点作为飞行器气动耦合可容忍上限,对应的耦合度称之为可控耦合度。

根据可控耦合度定义,在俯仰通道中,若飞行器升降舵满偏所产生的俯仰力矩刚好有效平衡稳定力矩和稳定耦合力矩之和时(稳定力矩与耦合力矩同极性是最恶劣情况),则满足:

(10)

解得可控耦合度为:

(11)

式中,L为可控耦合度。

根据稳定力矩强耦合上界和下界值,定义稳定力矩强耦合的耦合度区间为:

(12)

4 针对气动强/弱耦合的解耦方法

4.1 飞行器气动弱耦合下气动解耦

根据定义,气动弱耦合表示飞行器某通道所受到耦合力矩与本通道的主力矩之比不大于kb。气动弱耦合下,气动耦合对飞行器的影响很小。在工程实际中,对于较小的耦合作用,可直接忽略。基于忽略耦合后的解耦对象设计控制器,保留一定的稳定裕度和鲁棒性能,可以有效应对实际对象中存在的较小通道间耦合作用。

如果俯仰通道中气动耦合满足:

(13)

则式(1)所示气动力矩简化为:

(14)

4.2 飞行器气动强耦合下气动解耦

根据气动强耦合的定义,气动强耦合的下界为耦合度kb,上界为保证飞行器各通道不至于失控的可控耦合度(K)L。以俯仰通道为例,飞行器为气动强耦合下,耦合力矩项对系统影响较大,不能直接忽略,需要将飞行器各通道的稳定力矩耦合项、操纵力矩耦合项或阻尼力矩耦合项等效为本通道相应的气动力矩项。具体方法为:

若稳定力矩耦合为强耦合,则等效为:

(15)

若操纵力矩耦合为强耦合,则等效为:

(16)

若阻尼力矩耦合为强耦合,则等效为:

(17)

以上各式右侧极性由耦合力矩和对应力矩的实际极性确定。

如果俯仰通道中气动耦合满足:

(18)

利用式(15)～式(17)可将通道稳定、操纵和阻尼耦合力矩分别表示为本通道的稳定力矩、操纵力矩和阻尼力矩。则式(1)所示气动力矩转化为:

(19)

在一定飞行弹道区间内,若飞行器的气动角变化很小,耦合力矩等效系数可近似为分段常值函数,从而有效地将气动耦合力矩项消除。气动耦合模型解耦方法流程如图1所示。

图1 气动耦合解耦方法流程Fig.1 Decoupling method of aerodynamic coupling process

5 算例分析

根据图1所示飞行器气动耦合解耦流程,以某飞行器为研究对象,验证所提气动解耦方法的合理性和有效性,验证思路如图2所示。

图2 气动耦合解耦方法验证思路Fig.2 Verification of decoupling method

针对飞行器下压段三自由度弹道仿真,选取特征点。以特征点1为例,通过CFD计算和气动工程估算,建立对象气动力矩模型表征形式为:

结合对象飞行器标称气动数据,计算飞行器特征点处三通道气动耦合度如表2所示。

表2 算例飞行器的气动耦合度Table 2 Aerodynamic coupling degree of example vehicle

与原始气动力矩模型相比,解耦后各通道不含气动耦合项,只包含本通道自身的力矩项,实现了三通道间气动解耦。但当气动模型中存在不确定性因素Δ时,通道间仍将存在气动残余耦合。

针对特征点处气动解耦模型,采用工程中最常用的PID控制方法开展六自由度仿真。仿真初始条件为:H=25 km,Ma=6,α0=0°,β0=1°,φ0=10°。仿真结果如图3所示。

由图3可以看出,迎角曲线能够快速地跟踪指令迎角,末段由于气动参数不确定性因素Δ的存在,迎角曲线在指令值附近抖动;侧滑角以及倾斜角曲线能快速收敛,控制效果保持较好;与理想弹道相比,理论弹道落点偏差小于7 m。

图3 输出性能指标对比Fig.3 Contrast of the output performance indexes

6 结束语

基于气动耦合评价指标——气动耦合度定义,划分了气动强/弱耦合的耦合度区间,分别提出了耦合忽略和等效转换解耦方法,使得气动耦合下模型可采用工程中常用的SISO控制系统设计与评价方法。仿真结果验证了所提出的面向控制的飞行器气动耦合模型解耦方法的有效性,该方法也可以推广到惯量耦合解耦分析中。

[1] 王自勇,牛文,李文杰.2012年美国高超声速项目进展及趋势分析[J].战术导弹技术,2013,(1):6-13.

[2] 吴宏鑫,孟斌.高超声速飞行器控制研究综述[J].力学进展,2009,39(6):756-765.

[3] Costa R R Da,Chu Q P,Mulder J A.Reentry flight controller design using nonlinear dynamic inversion[J].Journal of Spacecraft and Rockets,2003,40(1):64-71.

[4] 胡跃明.非线性控制系统理论与应用[M].北京:国防工业出版社,2005:76-91.

[5] Patil M J.Decoupled second-order equations and modal analysis of a general nonconservative system[R].AIAA-2000-1654,2000.

[6] 刘玉忠,杨涤.用系统辨识方法简化飞行器自动驾驶仪模型[J].战术导弹技术,1995,(4):35-42.

[7] 周军,周凤歧,李言俊.飞行器耦合通道控制系统的独立设计方法研究[J].宇航学报,1998,19(4):65-69.

[8] 严恒元,陈劲松,冯亚南,等.飞行器气动特性分析与工程计算[M].西安:西北工业大学出版社,1990:192-251.

[9] 苗瑞生,居贤铭,吴甲生.导弹空气动力学[M].北京:国防工业出版社,2006:463-509.

[10] Keshmiri S,Colgren R.Development of an aerodynamic database for a generic hypersonic vehicle[R].AIAA-2005-6257,2005.

[11] Engelund W C,Holland S D,Cockrell C E Jr.Aerodynamic database development for the hyper-X airframe-integrated scramjet propulsion experiments [J].Journal of Spacecraft and Rockets,2001,38(6):803-810.

[12] 高黛陵,吴麒.多变量频域控制理论[M].北京:清华大学出版社,1998:65-67.

[13] 刘晨辉.多变量过程控制系统解耦理论[M].北京:水利电力出版社,1984:98-100.

[14] (美)周克敏,(美)多伊尔.鲁棒与最优控制[M].北京:国防工业出版社,2006:245-249.

Researchoncontrol-orienteddecouplingmethodforvehicleaerodynamiccouplingmodel

ZHU Duo-bin, Hu Wei-jun, Lin Peng, Zhou Jun

(Institute of Precision Guidance and Control, NWPU, Xi’an 710072, China)

For the problems of complex design of vehicle control system, evaluation method for the existing control system which can not be used in control performance caused by aerodynamic coupling, this paper presents a new aerodynamic decoupling method. Firstly, with the definition of degree of the coupling introduced in this paper, the coupling characteristics are defined by the degree of the aerodynamics coupling. Then, the decoupling method is proposed under different aerodynamics coupling characteristics. Finally, the model of aerodynamic coupling is completely or partially decoupled, which is helpful for using the common SISO control system’s design and evaluation methods in engineering. This control-oriented decoupling method is proved to be efficient and correct through the analysis of an example vehicle’s decoupling.

aerodynamic coupling; degree of the aerodynamic coupling; control-oriented decoupling

TJ765.2

A

1002-0853(2013)05-0402-05

2013-03-01;

2013-05-28; < class="emphasis_bold">网络出版时间

时间:2013-08-21 18:47

高等学校博士学科点专项基金资助(20106102120008)

朱多宾(1988-)，男，安徽寿县人，硕士研究生，研究方向为导航、制导与控制。

(编辑：李怡)