改进的UPF方法及其在MUAV组合导航中的应用

邵玮, 祝小平, 周洲, 赵刚

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 无人机研究所, 陕西 西安 710065;3.西北工业大学 航天学院, 陕西 西安 710072)

改进的UPF方法及其在MUAV组合导航中的应用

邵玮1, 祝小平2, 周洲1, 赵刚3

(1.西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065;2.西北工业大学 无人机研究所, 陕西 西安 710065;3.西北工业大学 航天学院, 陕西 西安 710072)

针对微小型无人机组合导航系统中出现的非线性环节,以及微小型无人机特殊的飞行环境易导致GPS信号因受到遮挡而时断时续的情况,提出一种改进的无迹粒子滤波(UPF)方法。利用带有残差约束的自适应渐消方法对UPF进行约束和改进,通过加强最新量测信息在状态估计中的作用,达到迅速应对系统突变、减缓滤波器发散的目的,增强系统鲁棒性。仿真结果表明,相比于无迹卡尔曼滤波(UKF)和粒子滤波(PF),该方法能有效改善滤波性能、抑制滤波发散、提高组合导航系统的定位精度,且在GPS重新捕获信号时具有更快速的重定位能力。

微小型无人机; 组合导航; 无迹粒子滤波; 自适应渐消滤波

0 引言

微小型无人机(Micro Unmanned Aerial Vehicles, MUAV)组合导航系统中通常会存在一定的非线性环节,其微惯导(MEMS-SINS)/GPS组合导航系统伪距/伪距率组合方式中的量测方程即为非线性方程,在这种情况下,使用线性卡尔曼滤波(KF)方法很难解决导航数据融合的问题。

目前,解决组合导航系统中非线性模型滤波问题时使用较多的方法有两类:一类是近似求解非线性函数,将系统方程中的非线性部分线性化,忽略或逼近高阶项的方法,如扩展卡尔曼滤波方法(EKF);另一类是利用采样的方法近似求解非线性密度函数,从而得到状态量的后验估计值,如无迹卡尔曼滤波方法(UKF)[1]和粒子滤波方法(PF)[2]。文献[3]将UKF方法应用于GPS/SINS组合导航系统,通过与KF方法和自适应滤波方法相比较,证明UKF方法提高了滤波精度。文献[4]设计了一种基于交互多模型的UKF算法,用于解决GPS/DR组合导航系统中的非线性问题,相比于单个UKF方法,其具有估计精度高、适用于动态系统等特点。上述研究均在认定系统可以时刻捕获GPS信号的情况下进行的,然而MUAV常穿梭于建筑物内部、城市巷道等复杂环境中执行任务,这样的飞行环境会对GPS信号的接收产生很大影响,造成GPS信号时断时续,从而导致组合导航系统出现模型误差增大和量测信息发生较大突变的情况。

针对这一问题,本文以非线性滤波方法为基础,提出一种基于改进的UPF方法的MUAV组合导航算法。通过在粒子滤波框架下使用UKF方法产生更加准确的重要性分布,利用带有残差约束的自适应渐消方法对UPF进行约束和改进,使系统充分利用最新量测信息,在GPS失效时能够快速反应,减缓滤波发散的速度;同时有效减轻了粒子退化及贫化问题,提高了滤波精度。

1 自适应渐消滤波

自适应渐消滤波是一种能够有效利用系统最新量测信息,并可根据一定条件对参数进行自适应调节的滤波方法。根据渐消滤波思想,通过适当地改变协方差阵的权值,乘以一个加权因子,即可增强当前量测数据在状态估计中的作用,以应对系统的突变及漂移,达到避免滤波器发散的目的。根据式(1)约束条件得到,多重次优渐消因子是设计残差约束自适应渐消滤波的关键[5]。

(1)

这种方法使误差序列在每一步相互正交,以此作为约束,使滤波器能够自主校正估计误差。通常情况下,上述条件很难满足,只能要求等式近似成立即可,于是有:

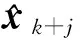
(2)

这样问题转化为选择一个合适的渐消矩阵,使得Cj,k中(Pxkzk-KkC0,k)一项为0,根据渐消思想可知一步预测状态方程为[6]:

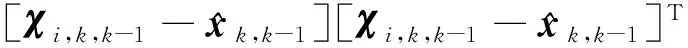
(3)

ηi,k=max{1,αick}

(4)

其中:

ck= tr[C0,k]/{tr{diag[α1,α2,…,αn]×

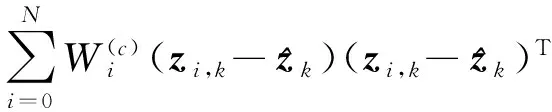
(5)

式中,C0,k为误差阵,更新公式为:

(6)

式中,0<ρ≤1为遗忘因子。

2 带有残差约束的自适应渐消UPF方法

在非线性系统中,本文将自适应渐消滤波和UPF方法相结合,提出一种改进的UPF方法。该方法结合了UKF和PF的优点,用UKF方法产生的Sigma点作为采样点,对状态向量后验分布进行近似,提高了粒子滤波效果;而带有残差约束的自适应渐消滤波则充分利用系统最新量测信息,使系统具有更好的应对突变的能力。

带有残差约束的自适应渐消UPF方法的具体步骤如下:

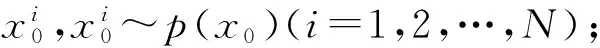
(7)

各个Sigma点的权值分别为:

(8)

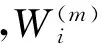
(3)时间更新:利用UKF算法对粒子进行预测更新,由系统状态方程对每个Sigma点进行非线性变换并进行加权处理,有:

(9)

一步预测均方误差为:

(10)

zk| k-1=h(χk| k-1)

(11)

(12)

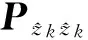
(13)

(14)

计算滤波增益阵:

(15)

在此处引入带有残差约束的自适应渐消滤波方法,利用渐消UKF思想计算渐消因子,根据式(1)的约束条件,可以求得状态更新后的滤波值和状态后验方差阵分别为:

(16)

(17)

(18)

式中,i=1,2,…,N。归一化权值,有:

(19)

(20)

(21)

(22)

(7)计算状态估计:

(23)

返回第(2)步重复上述过程。

通过以上步骤可以看出,该方法由于考虑了当前最新量测信息的影响,因而能够进一步提高滤波精度,有效地提高MUAV的导航定位精度;利用带有残差约束的自适应渐消方法对UPF改进后,使MUAV能应对系统状态突变,当MUAV重新捕获GPS信号时,该方法能够使滤波值迅速收敛。

3 组合导航系统数学模型

本文中MUAV的MEMS-SINS/GPS组合导航系统采用伪距/伪距率工作方式,其特点是量测方程为非线性,因此本文先以采用这种方式的MUAV组合导航系统为研究对象,建立滤波模型。

3.1 系统状态方程

取MEMS-SINS的导航输出参数误差和微型GPS接收机的误差状态作为系统状态,将微惯性传感器的误差考虑进来,可得20维系统状态方程为:

(24)

式中,W为噪声向量;F和G分别为状态系数矩阵和误差系数矩阵。且有:

=[φEφNφUδvEδvNδvUδLδλ

δhεbxεbyεbzεrxεryεrz

(25)

式中,状态量φE,φN,φU,δvE,δvN,δvU,δL,δλ,δh分别为微惯导平台误差角、速度误差和位置误差;εb和εr分别为微陀螺漂移误差中的随机常数误差和一阶马尔柯夫过程随机误差;为微加速度计漂移误差中的一阶马尔柯夫过程随机误差;δtu为时钟误差引起的等效距离误差;δtru为时钟频率误差引起的等效速度误差。

3.2 系统量测方程

组合导航系统以微型GPS接收机给出的伪距、伪距率信息为观测量,假设MUAV在地球坐标系(e系)下真实坐标为(x,y,z),MEMS-SINS给出的MUAV在e系下坐标为(xI,yI,zI),第j颗卫星在e系中坐标为(xsj,ysj,zsj),则MEMS-SINS给出的MUAV的位置所对应于第j颗卫星的计算伪距为:

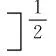
δtu+vρj(j=1,2,3,4)

(26)

式中,vρj为伪距测量误差。

同理,MEMS-SINS给出的MUAV速度所对应于第j颗卫星的计算伪距率为:

(27)

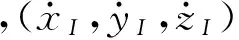
在导航定位中,MUAV在e系中的位置通常用地理经度、纬度和高度表示。为方便计算,可利用坐标转换公式将其转换为空间直角坐标,转换过程详见文献[8],此处不再赘述。

最后得到系统量测方程为:

(28)

4 仿真结果及分析

为了验证本文所提算法,对其进行计算机仿真。结合MUAV的实际情况,选取东北天地理坐标系作为导航坐标系,设定仿真条件为:MUAV初始位置为北纬34.2°,东经108.7°,飞行高度100 m,初始航向角35°,初始俯仰角和滚转角均为0°,飞行轨迹包括起飞、爬升、平飞、转弯等;微陀螺仪常值漂移10(°)/h,随机噪声均方差10 (°)/h;微加速度计常值误差1×10-3g,随机误差均方差2×10-4g;微型GPS接收机随机伪距测量误差为15 m,随机伪距率测量误差0.1 m/s;接收机时钟偏差为20 m,时钟偏差噪声为0.1 m/s。仿真时间1 800 s,组合导航系统滤波周期为1 s。设定在600 s时GPS停止工作,800 s时恢复,将本文方法与UKF方法和PF方法进行比较,三种方法的仿真结果如图1所示。

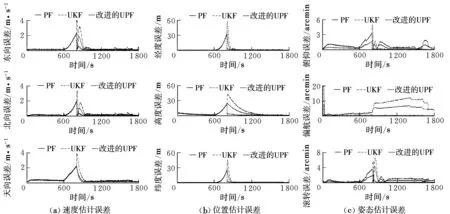
图1 三种方法仿真结果比较Fig.1 Comparison of simulation results obtained with the three methods

由仿真结果可以看出,所提方法在速度估计误差、位置估计误差和姿态估计误差等方面比UKF方法均有较大程度的改进;在位置估计误差、姿态估计误差两方面较标准PF方法有一定改进;在速度估计误差方面效果与PF方法接近。该方法可将东向、北向和天向速度的估计误差分别控制在0.15 m/s,0.15 m/s和0.2 m/s以内;位置估计误差在5 m以内;俯仰角、滚转角估计误差在0.2 arcmin左右,偏航角估计误差在0.8 arcmin左右。

5 结论

(1)与传统的PF方法相比,改进的UPF方法能够比普通的粒子滤波方法更准确地逼近状态向量的后验分布,提高了滤波精度。

(2)对系统状态突然发生变化的情况具有良好的反应能力;通过渐消因子自适应的调节权值,使有效信息得以充分利用,较好地抑制了滤波发散,增强了系统的鲁棒性;在GPS能够正常使用的情况下,该方法可使系统具有更精确的导航能力。

(3)采用权值优选算法克服粒子滤波中常出现的粒子贫化问题,较好地保持了粒子的多样性。

(4)该方法具有较为适中的计算量,能够满足MUAV组合导航系统对实时性的要求。

[1] Julier S,Uhlmann J,Durrant-Whyte H F.A new method for the nonlinear transformation of means and covariance in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477-482.

[2] 朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010:27-32.

[3] 鲍其莲,周媛媛.基于UKF的GPS/SINS伪距(伪距率)组合导航系统设计[J].中国惯性技术学报,2008,16(1):78-81.

[4] 臧荣春,崔平远,崔祜涛,等.基于IMM-UKF的组合导航算法[J].控制理论与应用,2007,24(4):634-638.

[5] 刘铮.UKF算法及其改进算法的研究[D].长沙:中南大学,2009.

[6] 周东华,席裕庚,张钟俊.一种带多重次优渐消因子的扩展卡尔曼滤波器[J].自动化学报,1991,17(6):689-695.

[7] 张琪,胡昌华,乔玉坤.基于权值选择的粒子滤波算法研究[J].控制与决策,2008,23(1):117-120.

[8] 刘建业,曾庆化,赵伟,等.导航系统理论与应用[M].西安:西北工业大学出版社,2010:350-354.

ImprovedUPFalgorithmanditsapplicationinINSofMUAV

SHAO Wei1, ZHU Xiao-ping2, ZHOU Zhou1, ZHAO Gang3

(1.National Key Laboratory of Special Technology on UAV, NWPU, Xi’an 710065, China;2.The UAV Research Institute, NWPU, Xi’an 710065, China;3.College of Astronautics, NWPU, Xi’an 710072, China)

In allusion to the nonlinear component in INS of MUAV, and the intermittent GPS signal caused by serious sheltering in special flight environment, an improved unscented particle filter (UPF) method is proposed. The UPF is constrained and improved by using self-adaptive fading method with residual constraints. By strengthening the effect of the new measurements in state estimation, the purpose of quick response to the sudden changes of the system and filter divergence slowed down could be reached and the system robustness is enhanced. The simulation results show that, compared with UKF and PF, the new method can effectively improve the filter performance, suppress the filter divergence, enhance the positioning precision of the integrated navigation system, and reposition more quickly when GPS recaptures the signals.

micro UAV; integrated navigation; unscented particle filtering; self-adaptive fading filtering

V249.328

A

1002-0853(2013)05-0462-05

2013-05-23;

2013-06-03; < class="emphasis_bold">网络出版时间

时间:2013-08-21 18:46

邵玮(1982-)，女，陕西西安人，博士研究生，主要研究方向为无人机组合导航及飞行控制。

(编辑：李怡)