倾转机身无人机俯仰角奇异问题研究

路平, 肖文健

(军械工程学院 无人机工程系, 河北 石家庄 050003)

倾转机身无人机俯仰角奇异问题研究

路平, 肖文健

(军械工程学院 无人机工程系, 河北 石家庄 050003)

针对传统四元数向欧拉角转换公式的奇异性,分析了尾坐式垂直起降无人机在倾转机身时俯仰角奇异的问题,提出一种新的四元数向欧拉角转换方法。将双欧法与四元数法相结合,利用正欧拉角与反欧拉角奇异倒挂的特点,克服了传统四元数向欧拉角转换时俯仰角出现的奇异性。仿真结果表明,该方法实现了俯仰角在全角度范围的变化,有效地解决了尾坐式垂直起降无人机在倾转机身时俯仰角奇异的问题。

倾转机身; 四元数; 双欧法; 奇异性; 全角度

0 引言

垂直起降飞行器对跑道无依赖,且具有可悬停的优势;与传统直升机相比,垂直起降飞行器具有更高的前飞速度、更远的航程。正因为具备这些优点,垂直起降飞行器尤其适用于需要悬停或对起降场地有特殊要求的场合。目前,垂直起降飞行器有许多种类,如英国的“鹞”式垂直起降飞机、美军的V-22双倾转旋翼飞机。“鹞”式飞机通过调整尾喷管方向来实现垂直起降,V-22则通过安装在飞机上部两侧的两个可倾转旋翼来实现这一功能。最近,一种新型尾坐式垂直起降方案引起人们的关注,采用机尾坐地式垂直起飞,达到一定高度后转入平飞。降落时先爬升且机头向上,随后减小推力垂直降落。这种方式结构简单、质量轻,尤其适用于不必考虑空乘人员生理极限的无人机。这种尾坐式无人机在起飞时俯仰角接近或超过90°,此时欧拉角定义的奇异性将给飞行器姿态的解算带来一系列问题。目前,克服欧拉角奇异性的方法主要有四元数法和双欧法等。捷联惯导多采用四元数来表示飞行器姿态,这样可以避免欧拉角带来的奇异。但是由于欧拉角比四元数更加直观,往往要将四元数转换为欧拉角,而在传统四元数向欧拉角转换的过程中又引入了奇异[1]。20世纪70年代末,中国的科技工作者提出了解决欧拉方程奇异性的双欧法,并从理论上对此方法进行了深入的论证,研究和计算结果表明,应用双欧法能够有效解决欧拉角的奇异问题[2-3]。但是,双欧法在解正反欧拉方程时会涉及大量三角函数计算,显然对于多采用嵌入式系统的微小型飞行器很难快速完成这么大的计算量。

本文将讨论如何将四元数法与双欧法相结合,实现俯仰、滚转和航向三轴欧拉角的全角度测量,以解决尾坐式垂直起降无人机在倾转机身时俯仰角奇异的问题。

1 奇异性研究

1.1 尾坐式无人机起降原理

尾坐式无人机采用尾坐式停放,以直升机模式垂直起飞。达到允许高度后,自动倾斜器前倾并配合升降副翼下偏,由此产生低头力矩使无人机转入固定翼飞机模式平飞。降落时,无人机爬升并使机头竖直向上,然后协调减小旋翼总距及转速,缓慢垂直下降直至着陆。起降过程如图1所示。

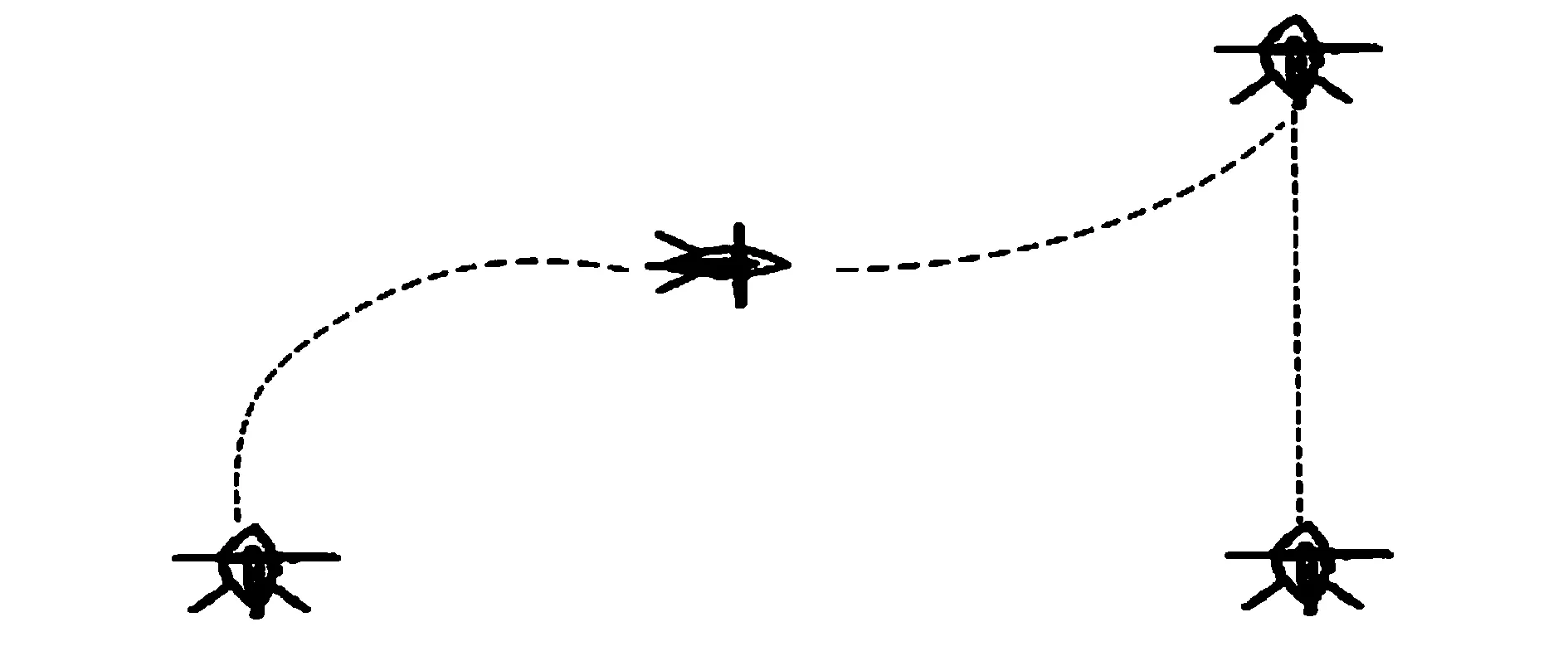
图1 尾坐式无人机起降过程Fig.1 Process of tail seated UAV taking off and landing

从图1可以看出,这种垂直起降的无人机起降时机头垂直向上,俯仰角接近甚至超过90°,而通常俯仰角的定义为-90°～90°。当俯仰角接近或者超过90°时,欧拉角法或四元数法在解算姿态角时都会不同程度地出现奇异问题,这给无人机飞行姿态的解算带来很大问题。

1.2 欧拉角法

确定载体的姿态,就是确定载体坐标系和大地坐标系之间的关系。在起始时刻两坐标系重合,经过绕z-y-x三轴转动到达新的坐标系,称三次转动角ψ,θ,φ为正欧拉角。由文献[4]提供的载体坐标系中角速度与正欧拉角的关系式得到正欧拉方程为:

(1)

由式(1)可以看出,当俯仰角θ趋近±90°时,第二项将趋于无穷而无法计算。当θ趋近0°或±180°时,方程解的精度较高。

当确定载体的姿态时,选取另一套与上述正欧拉角转动顺序不同的欧拉角θr,ψr,φr,其转动顺序为y-z-x,称此欧拉角为“反欧拉角”,为了与上述正欧拉角区别用下标r表示。其对应的“反欧拉方程”为[5]:

(2)

由式(2)可以看出,仅对反欧拉方程而言,也存在奇异性问题。当偏航角ψr趋近±90°时,第一项将趋于无穷而无法计算,方程出现奇异性。当ψr趋近0°或±180°时,方程解的精度较高。

1.3 四元数法

四元数形式的运动方程[6]为:

(3)

式中,q0,q1,q2,q3为描述飞行器姿态的四元数;ωx,ωy,ωz分别为飞行器绕x,y,z轴的角速度。

由于式(3)为线性微分方程组,所以没有奇异性。但是四元数描述飞行器姿态不够直观,当求出四元数q0,q1,q2,q3的值时,很难直观反映出此时飞行器的姿态。所以通常把四元数转化为欧拉角,其转化公式为:

(4)

由式(4)可知,俯仰角只能在-90°～90°之间取值,若俯仰角超过这个范围,则出现奇异。

2 全角度姿态角解算方法分析

由1.2节中对正反欧拉角的分析可以看出,正反欧拉方程都存在奇异性的问题,但两个出现奇异性的位置并不一样。如果综合考虑,能够避免欧拉方程在奇异处求解,即为“双欧法”[7]。

将出现奇异的角度附近区域称为奇异区,欧拉方程解的精度较高区域称为精华区。如果以±45°和±135°为界,可将0°～360°的区域按图2所示划分。

从图2可以看出,正、反欧拉方程之间精华区和奇异区存在倒挂的关系。双欧法正是基于这种思想并利用了这种倒挂关系,既摆脱了单组欧拉方程会出现奇异性的困难,又运用正、反欧拉方程的精华区提高了解算精度。

图2 正、反欧拉方程精华区与奇异区Fig.2 Essence and singular area of Euler equation

利用双欧法虽然能解决姿态解算时出现的奇异性问题,但是采用欧拉角进行姿态解算会涉及大量三角函数的运算,影响了算法的实时性。通过1.3节的分析可以看出,在四元数进行姿态解算时没有过多的三角函数运算,且在计算过程中不会出现奇异,仅在四元数转欧拉角时引入了奇异性。所以采用四元数进行姿态解算,在四元数转欧拉角时,借鉴双欧法的思路来解决出现奇异的问题。

由正欧拉角表示的从大地坐标系到载体坐标系的变换矩阵[8-9]见式(5),由反欧拉角表示的从大地坐标系到载体坐标系的变换矩阵见式(6)。

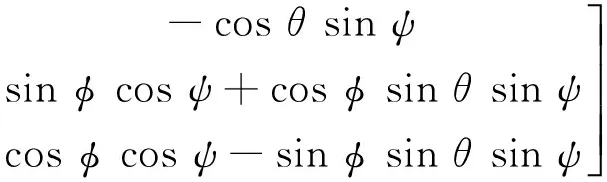
(5)

(6)

由四元数表示的从大地坐标系到载体坐标系的变换矩阵为:

(7)

因为从大地坐标系到载体坐标系的变换矩阵是唯一的,所以式(5)、式(6)和式(7)的右端矩阵相等,由此可以得到不同的四元数与欧拉角的转换关系。四元数与正欧拉角的转换关系为式(4),与反欧拉角的转换关系见式(8),通过式(4)和式(8)把四元数与双欧法结合起来。

(8)

在姿态解算过程中采用四元数法,避免了双欧拉角法中三角函数运算量大的问题;在解算结果输出过程中,通过采用双欧法推出不同条件下的欧拉角转换公式,避免了奇异性问题的出现。

3 全角度姿态角解算流程

全角度姿态角解算过程包括两套四元数转欧拉角的运算。四元数更新过程依据上一次四元数以及当前传感器数据进行更新运算,与解算出的欧拉角无关。当俯仰角的变化超过±45°时，将引起两套四元数转欧拉角公式的变换。因为前后两次姿态角解算之间俯仰角的变化非常小,所以在算法中采用上一次的俯仰角作为判断。其具体求解流程如图3所示。

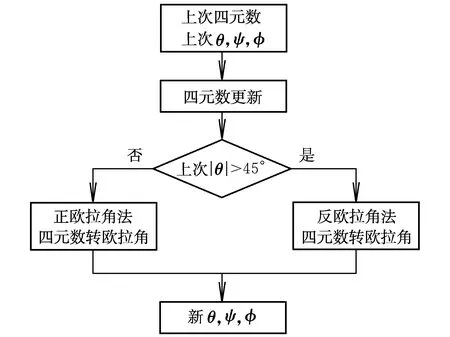
图3 全角度姿态角解算流程图Fig.3 Full-scale attitude angle resolving process

4 试验结果与分析

本文以某微小型无人机的航姿测量系统为平台,进行姿态解算得出姿态角。该系统由控制器、陀螺仪、加速度计和磁强计组成,控制器通过采集传感器数据进行姿态解算,并得出姿态角。为了验证该全角度姿态解算方法的效果,先不加入上述算法,直接将系统解算出的四元数转换为欧拉角输出。保持滚转角和偏航角为零,逐渐增大俯仰角,并记录三个欧拉角的变化情况;然后在系统中加入上述全角度姿态解算方法后,进行同样的仿真,并记录此时三个欧拉角的变化情况。记录仿真结果如图4所示。图中，姿态角采用不同线型表示,新方法通过加点以示区别。

图4 姿态角变化曲线Fig.4 Change of attitude angle

从图4可以看出,采用传统的方法,当俯仰角接近90°时,滚转角和航向角均出现突变,从0°分别变到-180°和180°。加入本文所述算法后，系统俯仰角在90°时没有了奇异性;俯仰角接近90°时,滚转角和航向角均没有出现突变的现象。

为了进一步验证该算法对俯仰角大幅度变化的跟踪性能,首先设定俯仰角持续跟踪幅度为175°的正弦信号,观测俯仰角输出以及误差情况,结果如图5所示。由图5可以看出,在俯仰角幅度连续大范围变化中,系统俯仰角跟踪效果良好,误差始终保持在±0.5°以内。

图5 俯仰角大范围变化跟踪曲线Fig.5 Tracking of pitch angle variation in wide range

5 结束语

将四元数与双欧法相结合可以有效地解决俯仰角在全角度范围内变化的跟踪问题,并且误差较小。此算法结合了四元数计算简单、欧拉角表示直观的优点,有效地解决了尾坐式垂直起降无人机在倾转机身时俯仰角奇异的问题,并且对于其他俯仰角变化幅度较大的飞行器也有借鉴价值。

[1] 登志红,付梦印,张继伟,等.惯性器件与惯性导航系统[M].北京:科学出版社,2012:20-135.

[2] 黄雪樵.克服欧拉方程奇异性的双欧法[J].飞行力学,1994,12(4):28-37.

[3] 熊志斌,刘喜斌.克服欧拉方程奇异性的方法研究[J].岳阳师范学院学报(自然科学版),2000,13(4):60-62.

[4] 陈廷楠,张登成.双欧法与四元数法的应用比较[J].飞行力学,1996,14(4):59-64.

[5] 张帆,曹喜滨,邹经湘. 一种新的全角度四元数与欧拉角的转换算法[J].南京理工大学学报,2002,26(4):376-380.

[6] 周亢,闫建国,屈耀红.全角度姿态角解算方法研究与仿真[J].系统仿真学报,2009,21(6):1697-1700.

[7] 王海峰,王成良.解决欧拉方程奇异性的方法探讨[J].飞行力学,2006,24(3):94-96.

[8] 袁绪龙,张宇文.运载器垂直出水弹道姿态角奇异性问题研究[J].弹箭与制导学报,2005,25(2):83-87.

[9] 周伟,张晓今,寇保华,等.双欧法在克服伞-弹系统欧拉方程奇异性中的应用[J].航天返回与遥感,2003,24(3):4-8.

ResearchonthepitchanglesingularityproblemoftiltingfuselageofUAV

LU Ping, XIAO Wen-jian

(Department of Unmanned Aerial Vehicle Engineering, Ordnance Engineering College,Shijiazhuang 050003, China)

For the singularity problem of transformation between quaternion and Euler, the pitch angle is singular when the vertical takeoff and landing (VTOL) UAV tilts the fuselage. A new transformation way between quaternion and Euler was proposed. This method utilized the inverse relationship between the ordinary and the reversed Euler equations and solved the singularity problem successfully. Simulation results show that this method could calculate the pitch angle in the full-scale and effectively solve the singularity problem when the VTOL UAV tilts the fuselage.

tilting fuselage; quaternion; Dual-Euler method; singularity; full-scale

V249.1

A

1002-0853(2013)05-0429-04

2013-01-23;

2013-04-06; < class="emphasis_bold">网络出版时间

时间:2013-08-21 16:14

路平(1961-)，男，河北石家庄人，教授，硕士生导师，研究方向为无人机通信链路与导航；肖文健(1989-)，男，河北张家口人，硕士研究生，研究方向为无人机姿态测量。

(编辑：李怡)