模糊综合评判在面实体匹配中的应用研究

熊天星 (新疆兵团勘测设计院(集团)有限责任公司，新疆 乌鲁木齐 830002)

模糊综合评判在面实体匹配中的应用研究

熊天星 (新疆兵团勘测设计院(集团)有限责任公司，新疆 乌鲁木齐 830002)

地图数据库合并是由同一地区2个或2个以上不同来源的地图数据库生成一个新的更好的地图数据库。面实体匹配是地图数据库合并的重要组成部分，综合分析常用的的面实体匹配方法，比较分析各自的优缺点，将模糊综合评判理论应用到面实体匹配中。通过试验实例，证明了其现实可行性，并与常用方法进行比较，证明了其优越性。

地图数据库合并；模糊综合评判；面实体匹配

地图数据库的各级应用部门，有时也需要将这些不同来源的地图数据库合在一起使用，因此研究城市地图数据库之间的实体匹配与合并技术是很有必要的[1]。现有的面实体匹配算法有整体-整体匹配(如面质心几何距离匹配法和模糊拓扑关系匹配法)和局部-整体匹配(如转向角函数面匹配方法)2大类。下面，笔者对模糊综合评判在面实体匹配中的应用进行了研究。

1 常用算法

1.1面质心几何距离匹配算法

面质心几何距离匹配算法通过质心来判断2个面的大致位置关系、通过面密度来判断它们的大致形状关系、通过面积来判断它们的大小差异来进行几何匹配。面质心几何匹配算法过程如下：先分析参与合并的数据库特点，将定位精度相对较高的作为参考图，属性信息相对较丰富的作为调整图，再求出调整图中面实体的质心点位置，利用点在面内的几何规则，判断该质心点是否在对应参考图中的某个面实体内，上述过程属于粗匹配。根据几何匹配方法的几何规则，利用多边形面积和面密度进行匹配检验，上述过程属于精匹配。经过粗匹配后选中的对应面实体，如果面积相等，还不能确定是否真正匹配，需要再结合面密度公式进行检验；如果面密度也基本相等，则可以认为是一对一(l∶1)的匹配关系，它们属于同名实体；如果参考图的多边形比对应的调整图多边形的面积明显要小，可以认为是多对一(M∶l)的匹配关系；反之，可以认为是一对多(1∶N)的匹配关系。对于多对一(M∶1)的匹配关系，需要进行2次检验来确定是否匹配正确，即把对应的多个多边形面积相加，看看它们的面积之和是否与对应的多边形面积相等，若相等，则是同名实体，否则就不是同名实体。对于一对多(l∶N)的匹配关系，可以通过人工交互来确定。质心匹配方法目前还不能解决多对多(M∶N)的复杂匹配类型[2]。

1.2面实体之间模糊拓扑关系匹配算法

拓扑关系“重叠”区分为“弱重叠”和“强重叠”，因而可以将空间拓扑关系归为2大类：第1类拓扑关系包括相离、相接和弱重叠；第2类拓扑关系包括强重叠、相等、覆盖，被覆盖、包含和被包含。“弱重叠”与“强重叠”的区分依据可以为：若2个面域内部相交的面积占最小面域面积的一半以上则归为强重叠，否则归为弱重叠，可通过下式计算确定[3]：

(1)

式中，AO,BO分别为2个多边形的内部区域；|AO|代表该区域的面积值。

若OF大于 0.5，则归为第2类拓扑关系，否则归为第1类拓扑关系。利用形态距离来计算2个面拓扑关系的隶属度，从而可以确定2个面实体之间拓扑关系。在地图数据库实体匹配与合并过程中，根据同名点

之间的距离值来确定2幅图的点位相对误差σ，然后根据σ来确定形态距离的隶属度函数，并根据隶属度的大小来确定最小和最大形态距离值的分类。

1.3转向角函数面匹配算法

转向角函数匹配算法原理如下：选取图形p的某一顶点作为参考点p1，t轴代表p1沿着多边形周边到多边形上各点的距离，θ轴代表各点沿着周边的转向角的叠加(见图1)。从p1点到p2点的距离为13.66，线段d的转向角为3π/4，这样依此类推，将每个线段边的距离和线段边的转向角反映到直角坐标系[4]。

图1 转角函数匹配模型

2 建立模糊综合评判的匹配算法模型

2.1模型计算依据

(2)

此时无论rij的值如何，ai∧rij的结果都不能大于ai，ai实际上没有起到加权的作用，而是起到“过滤”、“限制”的作用。在下一步运算中通过取大，在n个ai∧rij中只取一个最大值，淘汰了其他因素，故这种运算类型又称主元素决定型。

2.2模糊评判模型的建立

因素集为U={U1(因素1)，U2(因素2),…,Un(因素n)},评判集为V={V1(标准1)，V2(标准2),…,Vn(标准n)},再做总的综合评判得：

(3)

3 实例分析

根据模糊综合评判原理建立面实体匹配算法模糊评判模型。因素集为U={u1(面质心几何距离法)，u2(模糊拓扑关系分类法)，u3(转向角函数法)}。评判集为V={v1(匹配很好)，v2(匹配一般)，v3(匹配很差)}。权重向量为A=(a1,a2,a3)。在权重分配上，采用将符合条件的匹配实体与总计实体数量的比率作为其权重向量[6](如有100个匹配实体，面质心几何距离法匹配了30个，那么面质心几何距离法匹配的权重向量为0.3)，这样排除了主观因素，从而提高匹配精度和可靠程度。为了验证面实体综合匹配方法的正确性，以江西省东乡县某村1∶500的地籍图、地形图为参考进行匹配试验，参与匹配的实体个数为62个，其中1∶1的匹配个数为40个(见图2和图3)。2种图同名面实体的差异主要包括2方面：①对同一房屋要素(集)的解释不同，导致对房屋边界线的合并和分割的不同，在建筑物群的内部这种差异尤其明显；解释的差异还表现在同一个房屋在一个图中包含了小的附属结构，而另一幅图中则没有；②不同图的位置差异。从面实体匹配的角度而言，差异①更难确定，因为有时其与差异②往往混淆在一起。

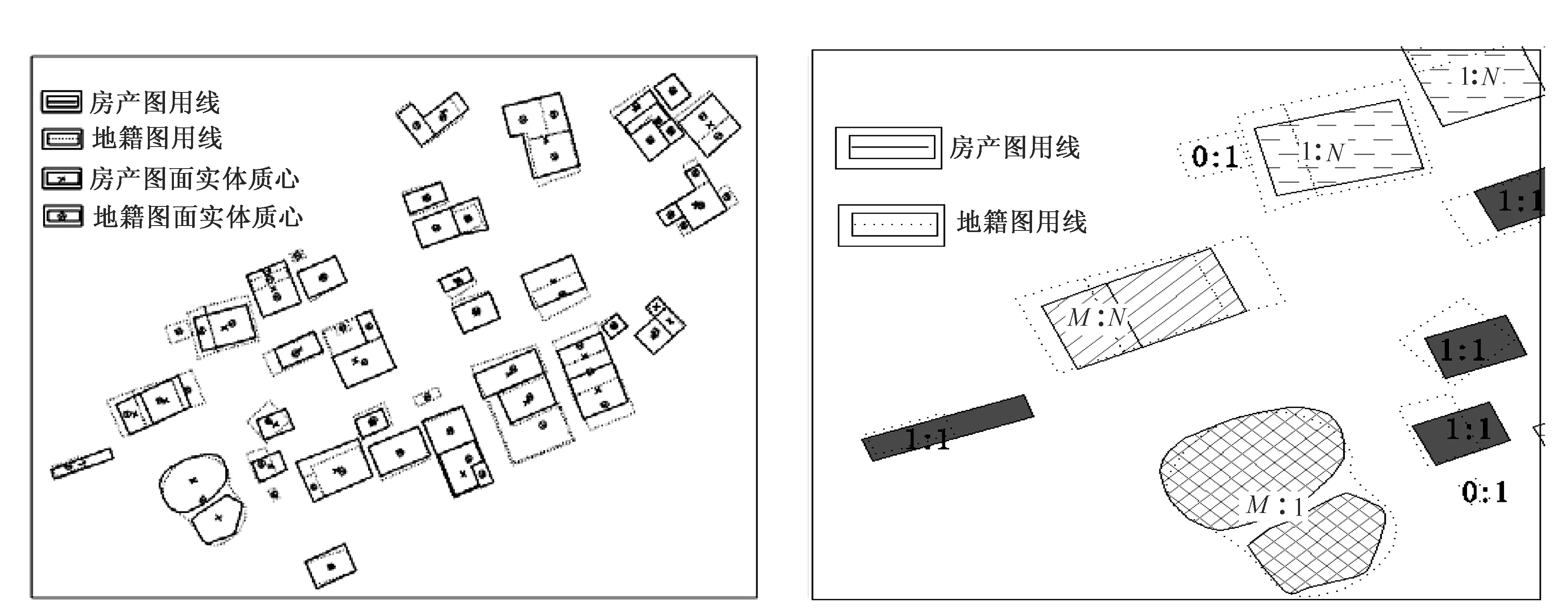
图2 匹配建筑物面实体质心显示图 图3 匹配建筑物面实体拓扑关系局部放大图

综合算法的匹配步骤如下：①按面质心几何匹配法的进行匹配，将1∶1面实体的匹配度在[0.9,1]以上的个数统计出；②将剩余的匹配实体按基于模糊拓扑关系的方法进行匹配，把匹配度在[0.9,1]以上的实体个数统计出；③剩余的匹配实体按转向角函数法进行匹配，把匹配度在[0.9,1]以上的实体个数统计出；④对完成以上步骤再剩余的实体，重复步骤①、②、③，其匹配精度定为[0.7,0.9]，依次类推，以下循环的匹配精度为[0,0.7]；⑤将以上的每步的匹配实体个数进行统计，建立统计结果表(见表1)，由权重分配方法得到权重分配表(见表2)；⑥根据权重分配表，得出每种算法的权重向量和评判矩阵，为模糊评判计算做好准备；⑦评判计算。根据参与计算的因素和要得到结果的特点，选择适当的评判计算方法。

表1 统计结果表

表2 权重分配表

由表2可得评判矩阵为：

按模糊综合评判的最大隶属度原则，综合算法的配准率在[0.9,1]之间，达到匹配很好的标准。

4 匹配算法比较

为了验证综合算法的实用性，将综合算法与单独使用面质心几何匹配法、模糊拓扑关系匹配法与转向角函数法进行比较运算，结果如表3所示。

表3 各算法独立匹配评判结果

由表3建立各算法独立匹配权重结果如表4所示。

表4 各算法独立匹配权重结果表

由表4得到各算法独立参与匹配的评判矩阵：

按最大隶属度原则，综合算法在匹配准确率上比其他算法独立匹配更有效，具体表现在在匹配类型和范围上，不但能处理所有的匹配类型，还可以处理变形和遮掩问题，既能顾全整体与整体的匹配，也可以考虑局部与整体的匹配。

5 结 语

在对3种常用的面实体匹配算法模型进行比较的基础上，提出模糊评判综合匹配算法，通过实例试验，证明模糊评判综合算法不但比其他算法具有更高的匹配准确率，而且能处理匹配类型以及变形和遮掩问题，因而能够应用在实际工作中。

[1]张桥平,李德仁,龚键雅.地图合并技术[J].测绘通报,2001,(7):50-53.

[2]丁险峰,吴洪,张宏江,等.形状匹配综述[J].自动化学报,2001,33(5):678-689.

[3]Winter S.Knowledge acquisition for the automatic interpretation of spatial data[J]. International journal of geographical information systems, 2000,14(1):1-4.

[4]章思亮,臧德彦.基于转向角函数的形状匹配算法[J].科技广场,2009,22(1):118-121.

[5]杨纶标.模糊数学原理及应用[M].第4版.广州：华南理工大学出版社,2008.

[6]黄涛.模板匹配在图像识别中的应用[J].云南大学学报(自然科学版),2005,27(5):327-332.

[编辑] 李启栋

O159

A

1673-1409(2013)25-0023-04

2013-06-24

熊天星(1982-)，男，助理工程师，现主要从事摄影测量与遥感方面的研究工作。