机动再入体的带落角约束扩展比例导引律设计

陶健, 陈洁,, 赵红超, 李世改

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100191; 2.海军航空工程学院 控制工程系, 山东 烟台 264001; 3.海军航空工程学院 训练部, 山东 烟台 264001)

机动再入体的带落角约束扩展比例导引律设计

陶健1, 陈洁1,2, 赵红超2, 李世改3

(1.北京航空航天大学 自动化科学与电气工程学院, 北京 100191; 2.海军航空工程学院 控制工程系, 山东 烟台 264001; 3.海军航空工程学院 训练部, 山东 烟台 264001)

传统的各种制导律都是以获得最小脱靶量为最终目标,没有考虑到导弹击中目标时刻的末端落角。为了保证非自旋再入体完成精确打击目标的任务,针对非自旋再入体垂直打击目标的制导问题,设计了一种带落角约束的扩展比例导引律。仿真研究表明,所设计的末制导律能够保证非自旋再入体命中目标时的脱靶量和末端落角都能满足要求,可以为开展近空间非自旋再入体制导问题的研究提供测试平台。

再入体; 带落角约束的末制导律; 机动; 精确打击

0 引言

机动再入体的精确打击能力一直受到各军事强国的高度重视,为了提高再入体的打击精度,需要在再入体上安装制导装置。机动再入体的打击目标主要是敌方机场、指挥中心、大型军舰、弹道导弹运输车、加固的地下工事等具有重大军事价值的目标,因此不仅希望再入体命中目标时能获得最小脱靶量,而且希望能以接近垂直下落的终端姿态打击目标,最大限度地发挥战斗部效能,取得最佳毁伤效果。这就需要在末制导律的设计中增加落角约束的指标要求。

近年来,许多研究者针对不同的工程应用问题,设计出了多种形式的带落角约束的制导律。文献[1]在经典比例导引律的基础上增加了时变偏置项来处理角度约束问题,其研究的前提条件是导弹速度为常量。文献[2]针对电视指令制导空地导弹,设计了满足落角约束的末制导律,其研究中假设导弹和目标的速度都为常量,将导弹自动驾驶仪视为一阶惯性环节,求得的扩展比例导引律形式比较复杂。文献[3-5]基于虚拟目标的思想,设计了不同形式的满足落角约束的扩展比例导引律,通过虚拟目标参数的设置来保证末端落角要求,虚拟目标设置的好坏对制导效果影响很大。文献[6]依据Lya-punov稳定性原理推导了一种扩展比例导引律,保证导弹以期望的大落角击中目标,在研究中假设导弹和目标的速度都为常量,并认为弹目距离变化率近似为常值。文献[7]研究了导弹垂直打击地面固定目标的自适应比例导引律,将三维空间制导问题分解为纵向平面和侧向平面的制导问题,采用自适应更新策略对导引系数进行调整。但以上研究大都针对特定的导弹对象,如何将现有技术应用进行扩展并加以工程化,成为当前研究的难点。基于此,本文针对非自旋再入体垂直打击地面固定目标或慢速运动目标的带落角约束制导问题进行了研究。

1 问题描述

非自旋再入体与前面研究的导弹相比有其特殊之处:(1)非自旋再入体的运动速度很大,在再入过程中仅受到重力和空气动力的作用,其速度是明显变化的,但不是常值;(2)弹头再入过程中的弹道倾角、弹目视线角都比较大,不满足制导过程中的小角度假设,因此不能对制导过程进行线性化处理。鉴于非自旋再入体的特殊性,设计了适用于非自旋再入体的三种形式的带落角约束的广义比例导引律。

为了简化制导问题,使求解的末制导律形式简单、工程上易于实现,提出如下假设:(1)非自旋再入体和目标均视为质点;(2)忽略非自旋再入体控制系统的动态特性,因为通常控制系统的动态特性要比制导系统的动态特性快得多。

2 带落角约束的扩展比例导引律

已有的文献研究的几种扩展比例导引律前提条件都是以导弹速度为常量,而非自旋再入体的运动速度变化很大,不能假设为常量。下面推导适用于非自旋再入体的扩展比例导引律形式。为了简化制导问题,将再入体-目标的相对运动关系分解为纵向平面内和侧向平面内的相对运动关系。

2.1 纵向平面的扩展比例导引律设计

在纵向平面内再入体-目标相对运动方程为:

(1)

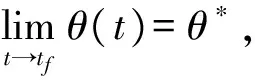
=0 (t=tf)

(2)

由制导几何关系可知:|θ*-q1|<90°,可得：

(3)

对式(1)的第2个方程求导,经整理可得:

(4)

(5)

构造Lyapunov函数为:

(6)

式中,c1>0。对上式求导可得:

(7)

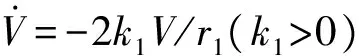
(8)

将f(x),g(x)的表达式代入式(8),整理得:

(9)

2.2 侧向平面的扩展比例导引律设计

在侧向平面内再入体-目标相对运动方程为:

(10)

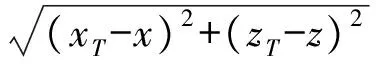
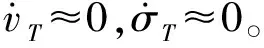
(11)

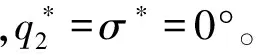
(12)

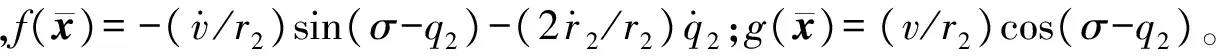
构造Lyapunov函数为:

(13)

式中,c2>0。根据Lyapunov稳定性理论,同理可得侧向平面的带落角约束的扩展比例导引律为:

(14)

3 仿真研究

为了检验所设计的带落角约束的扩展比例导引律的制导效果,以文献[8]的非自旋再入体模型为研究对象,进行仿真研究。以非自旋再入体再入下落到50 km高度时作为起始点开始仿真,假设在起始点飞行速度为2 300 m/s,弹道倾角θ为-25°,偏航角ψ和弹道偏角σ均为0°。首先进行惯性弹道仿真,惯性弹道也就是在两个质量块固定不动的情况下非自旋再入体的无控制飞行弹道;然后进行制导弹道仿真,并将所设计的扩展比例导引律与传统的比例导引律进行性能对比。

仿真实例1:打击固定目标的制导弹道仿真。非自旋再入体打击的目标为一般大型目标,脱靶量指标为不超过10 m。末端落角的期望值分别为:θ*=-90°,σ*=0°;末端落角要求分别为:-100°<θ(tf)<-80°,|σ(tf)|<2°。假设起始点弹头质心的侧向偏差为z=4 km,目标点位于:xT=90 km,yT=0 km,zT=0 km。当非自旋再入体由高度50 km下落到18 km时制导系统开始工作,导引弹头打击目标。

图1 采用比例导引律打击固定目标的仿真结果Fig.1 Simulation results of nonspinning reentry body attacking fixed target with PNG

由图1的仿真结果可知,采用比例导引律时,非自旋再入体打击地面固定目标的脱靶量为1.45 m,满足脱靶量指标要求;终端时刻非自旋再入体的弹道倾角为θ(tf)=-31.97°,弹道偏角为σ(tf)=1.58°。弹道倾角与期望值相差很大,不能满足末端落角要求。

下面采用上述的式(9)和式(14)的扩展比例导引律进行制导,导引再入体以期望的末端落角打击地面目标。通过仿真调试,确定制导律参数分别为:c1=0.045,k1=2.5,c2=0.08,k2=5.0。仿真结果如图2所示。

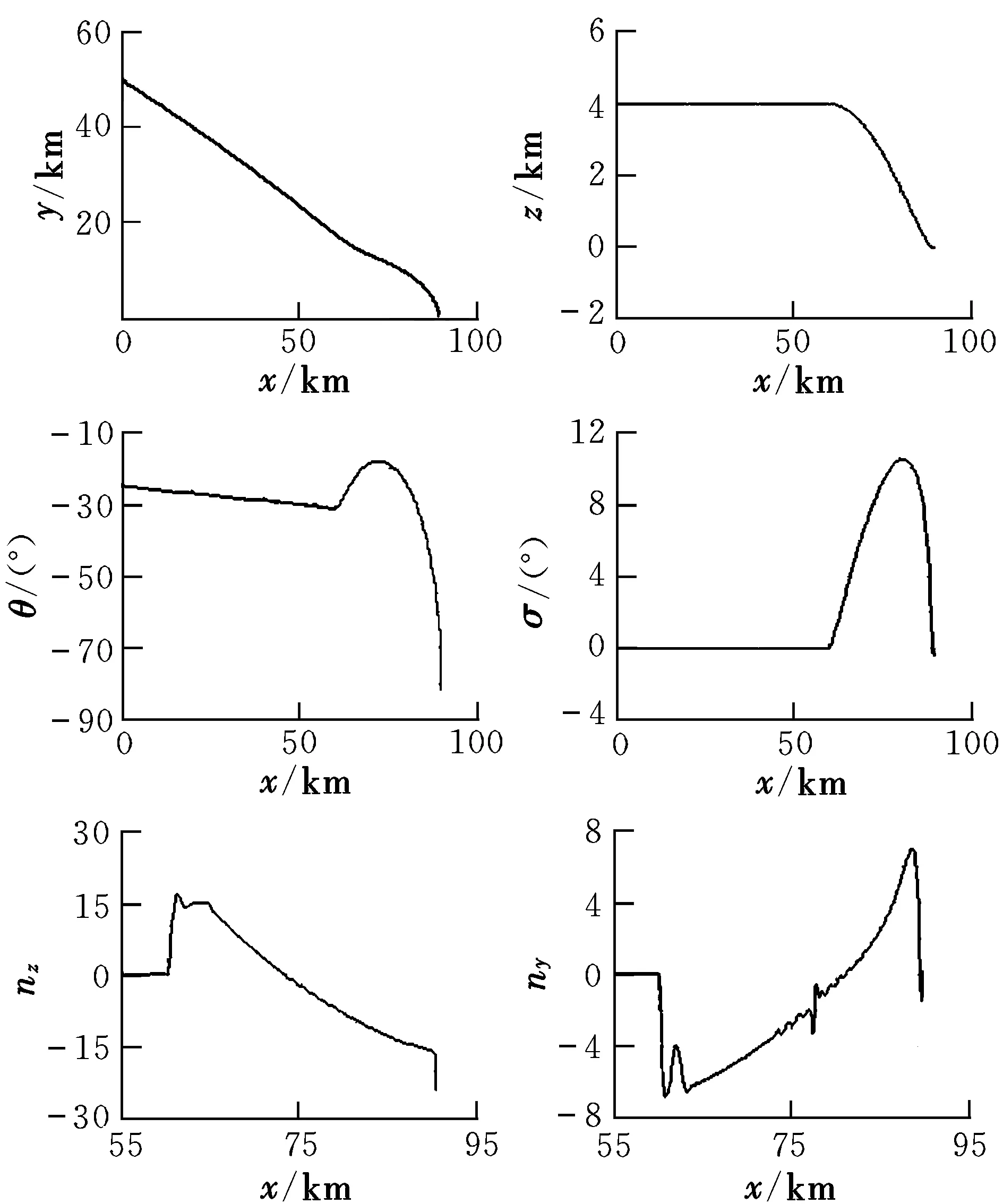
图2 采用扩展比例导引律打击固定目标的仿真结果Fig.2 Simulation results of nonspinning reentry body attacking fixed target with extended PNG

由图2的仿真结果可知,采用所设计的扩展比例导引律时,非自旋再入体打击地面固定目标的脱靶量为1.75 m,满足脱靶量指标要求;终端时刻非自旋再入体的弹道倾角为θ(tf)=-82.12°,弹道偏角为σ(tf)=-0.24°,同时也满足末端落角要求。由图可知,为了形成大角度攻击态势,非自旋再入体需要进行较大的弹道转弯,因此,制导过程中需要的机动过载比采用传统比例导引律时大很多。

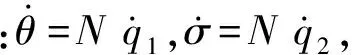
由图3的仿真结果可知,采用比例导引律时,非自旋再入体打击地面运动目标的脱靶量为1.12 m,满足脱靶量指标要求;终端时刻非自旋再入体的弹道倾角为θ(tf)=-29.94°,弹道偏角为σ(tf)=3.78°。弹道倾角与期望值相差很大,弹道偏角也超出了要求范围,不能满足末端落角要求。

图3 采用比例导引律打击运动目标的仿真结果Fig.3 Simulation results of nonspinning reentry body attacking moving target with PNG

采用所设计的扩展比例导引律进行制导,导引再入体以期望的末端落角打击运动目标。制导律参数仍然取c1=0.045,k1=2.5,c2=0.08,k2=5.0。仿真结果如图4所示。

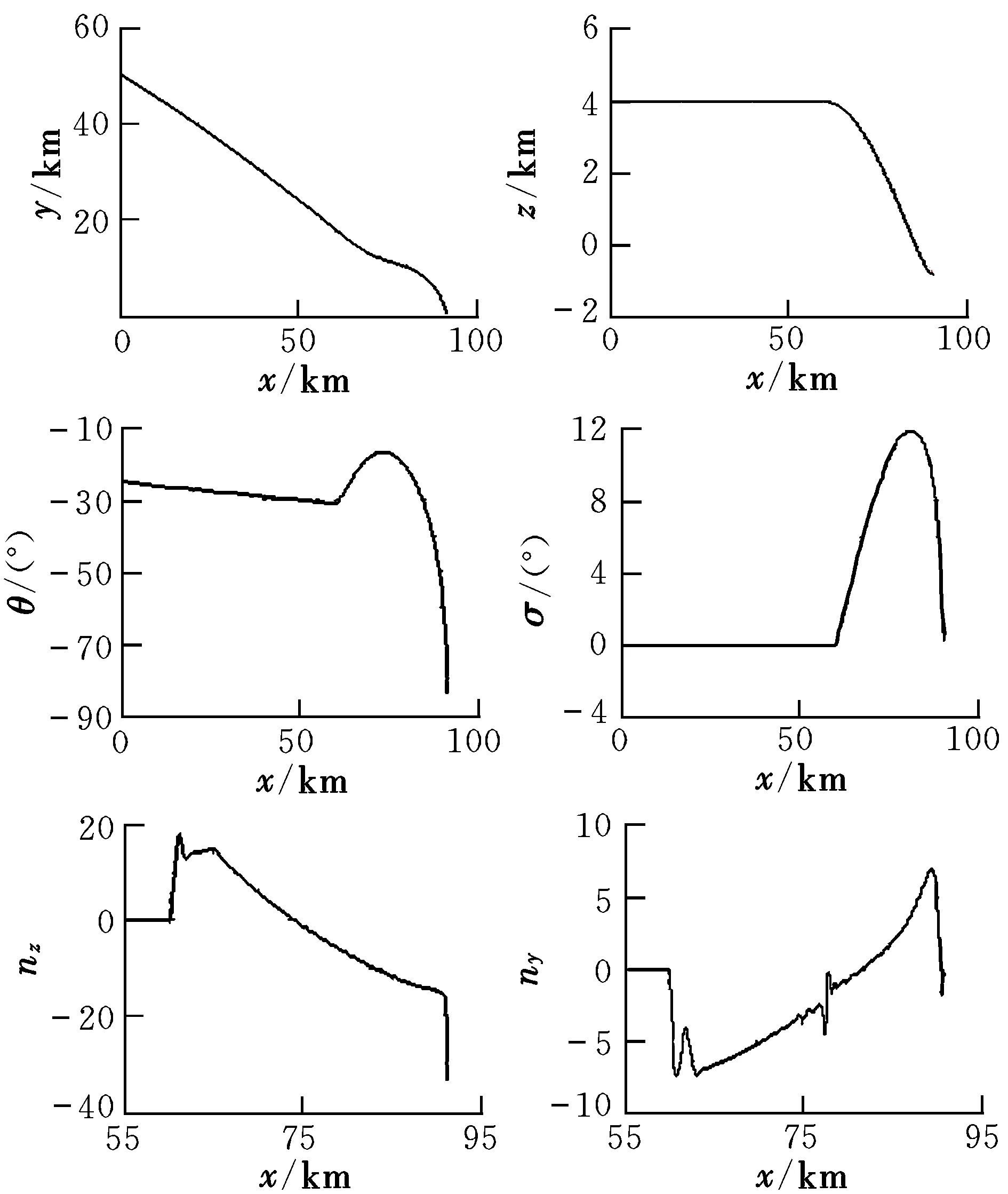
图4 采用扩展比例导引律打击运动目标的仿真结果Fig.4 Simulation results of nonspinning reentry body attacking fixed target with extended PNG

由图4的仿真结果可知,采用所设计的扩展比例导引律时,非自旋再入体打击地面运动目标的脱靶量为2.12 m,满足脱靶量指标要求;终端时刻非自旋再入体的弹道倾角为θ(tf)=-84.33°,弹道偏角为σ(tf)=0.92°,同时也满足末端落角要求。

4 结束语

针对非自旋再入体垂直打击地面固定目标或者慢速运动目标的制导问题,本文设计了非自旋弹头的扩展比例导引系统,将所设计的末制导律与传统的比例导引律进行对比仿真研究。国内对非自旋再入体的控制及导引的研究还不是很成熟,而且相关技术国内还没有得到工程应用,因此在此领域还存在许多理论问题和工程问题需要做进一步地深入研究。如何确定弹头纵轴与弹道间夹角的约束问题,将是下一步研究的内容。

[1] Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.

[2] 曹邦武,姜长生,关世义,等.电视指令制导空地导弹垂直命中目标的末制导系统研究[J].宇航学报,2004,25(4):392-396.

[3] 顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计[J].飞行力学,2006,24(2):43-46.

[4] 赵红超,顾文锦.基于Lyapunov稳定性的扩展比例导引律研究[J].飞行力学,2006,24(4):41-45.

[5] 张汝川,顾文锦,赵红超.带落角约束的超声速导弹制导方案研究[J].飞行力学,2009,27(3):45-49.

[6] 包一鸣,姜智超,彭琛,等.一种实现大角度打击的制导律设计[J].北京航空航天大学学报,2008,34(12):1375-1378.

[7] 胡正东,曹渊,蔡洪.一种打击地面固定目标的自适应比例导引律[J].系统仿真学报,2009,21(13):4084-4088.

[8] 李瑞康.再入体变质心动力学建模与仿真问题研究[D].哈尔滨:哈尔滨工业大学,2006.

Terminalguidancelawwithangularconstraintdesignformaneuveringreentrybody

TAO Jian1, CHEN Jie1,2, ZHAO Hong-chao2, LI Shi-gai3

(1.School of Automation Science and Electrical Engineering, BUAA, Beijing 100191, China; 2.Department of Control Engineering, NAAU, Yantai 264001, China; 3.Department of Training, NAAU, Yantai 264001, China)

In the traditional literatures, the aim of guidance law design was to obtain the minimum miss distance as the ultimate goal, without considering the limits from missile terminal angle when the missile hits the target. In order to ensure a nonspinning reentry body to complete the precise attacking task, we design one extended proportional navigation guidance law with terminal angle constraint for nonspinning reentry body vertical attack. Simulation research shows that above terminal guidance laws can ensure the nonspinning warhead to attack a target with required miss distance and required terminal angle,and provides a feasible test platform of nonspinning reentry body guidance system.

reentry body; terminal guidance law with angular constraint; maneuver; exact attack

TJ765

A

1002-0853(2013)04-0345-04

2012-05-22;

2013-05-07; < class="emphasis_bold">网络出版时间

时间:2013-06-06 13:21

国家自然科学基金资助(61004002);航空科学基金资助(20110184001);中国博士后科学基金资助(20110490266)

陶健(1982-),男,陕西商洛人,工程师,硕士,研究方向为控制理论与控制工程。

(编辑：方春玲)