鲁棒稳定性分析及其在飞行颤振试验中的应用

王东森, 吴志刚, 周友明

(1.中国飞行试验研究院 飞机所, 陕西 西安 710089； 2.北京航空航天大学 航空科学与工程学院, 北京 100191)

鲁棒稳定性分析及其在飞行颤振试验中的应用

王东森1, 吴志刚2, 周友明1

(1.中国飞行试验研究院 飞机所, 陕西 西安 710089； 2.北京航空航天大学 航空科学与工程学院, 北京 100191)

结合国内外的研究现状和工程应用需要,基于控制理论利用结构奇异值μ分析法将设计理论模型数据和实测试飞数据结合起来,可以在飞行试验过程中进行颤振边界预测,直接给出保守的颤振临界动压或者颤振临界速度,从而能够增加试验的安全性、缩短试飞周期、减少试验点并节省试验经费,是目前颤振试飞方法的有益补充。

颤振; 鲁棒稳定性; 结构奇异值; 颤振边界

0 引言

颤振飞行试验的主要目的是要验证飞机气动弹性稳定性边界是否满足相关设计要求[1-2]。由于颤振飞行试验存在激励力不足、测量点有限、数据信噪比低和模态稳定性水平低的特点,给模态参数识别带来非常大的困难,尤其是阻尼识别精度较差。另外,阻尼随飞行速度的变化呈非线性关系,阻尼外推曲线拟合还没有一个国内外公认通用的定量数学方法,传统颤振试飞最终结果一定程度上依赖于试飞技术人员的工程经验、技术水平等综合因素影响。

20世纪90年代末,美国学者提出了鲁棒颤振裕度分析方法[3],该方法降低了为扩展飞行包线而进行的飞行颤振试验的风险及试验成本,提高了颤振飞行试验的安全性和可靠性。本文讨论具体使用结构奇异值理论的工程方法并进行了实例计算[4]。

1结构奇异值理论(μ理论)

结构奇异值理论是鲁棒控制理论的一个分支[5]。任何含不确定性的控制系统经整理均可化为图1所示的P-Δ线性分式分析框架。

图中,P为广义的控制系统;Δ为结构不确定性算子;w为控制系统输入;z为控制系统输出,并且都与结构不确定性算子相关联。

在某一频率处,广义系统算子P∈Cn×n,不确定性算子Δ是由重复标量块和满块矩阵组成的复数块对角矩阵,其集合记为:

Δq):δi∈C,Δj∈Cmj×mj}

结构奇异值定义:复数矩阵P关于不确定性Δ的结构奇异值定义为:

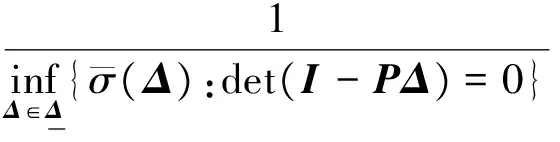
鲁棒稳定性定理:设α>0, 对于所有满足‖Δ‖∞

≤α的Δ(s),闭环系统鲁棒稳定的充分必要条件是结构奇异值的上界值满足:

(1)

2 飞机理论模型建立

弹性飞机系统颤振运动方程[6]为:

(2)

式中,q为与模态有关的广义坐标向量;M为广义质量对角阵;K为广义刚度对角阵;Q为广义非定常气动力系数矩阵。

2.1 非定常气动力系数拟合

给定的非定常气动力系数矩阵是一组与减缩频率相对应的离散形式,通常用拉氏变量描述的有理函数来近似非定常气动力。本文采用最小二乘(LS)法进行拟合。

气动系数矩阵Q的LS法有理函数近似式Qap为:

(3)

式中,Q0,Q1,Q2,Ej均为实系数矩阵;rj为实常数,称作气动力滞后根。另有:

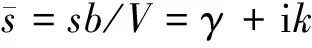
式中,b为参考长度;V为飞行速度;s=σ+iω,其中ω为振动圆频率,σ为运动衰减率。

Pyij=bij

(4)

式中,i=1,2,…,n;j=1,2,…,m;P中各元素为rj,kl的表达式;bij中各元素为F(kl),G(kl)的元素,均为已知。解关于式(4)的最小二乘问题可以得到拟合系数矩阵Q0,Q1,Q2,Ej中各元素值。

2.2 状态空间建模

将拟合得到的式(3)代入式(2),经过拉氏变换整理得到:

(5)

式中,xaj为气动力引起的附加状态向量,且有:

(6)

联立式(5)和式(6),得到以状态空间方程表达的飞机系统气动弹性运动方程:

简写为:

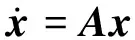
(7)

2.3 建模效果评估

本文算例取2个滞后根,以经典p-k法求得的颤振边界和以式(7)中状态矩阵A求取根轨迹得到的颤振边界之间的误差来衡量建模误差。由p-k法得到颤振边界为521.9 m/s,颤振频率为16.62 Hz;由根轨迹法得到颤振边界为523.1 m/s,颤振频率为16.62 Hz。两者颤振速度相对误差仅为0.22 %,颤振分支均对应平尾对称一弯模态。可见建模结果满足状态空间建模要求。

3飞机气动弹性系统μ框架建立与

分析

3.1 标称颤振μ分析系统

针对式(7)的飞机气动弹性系统,引入动压摄动,令:

(8)

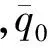
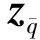
(9)

(10)

为便于表示及后续公式推导,将式(9)记为:

(11)

对上式进行拉氏变换得:

(12)

3.2 鲁棒颤振μ分析框架建立

由飞行试验测得的响应数据通过数据处理,可以辨识出相关模态的频率和阻尼并转化为系统特征值形式,因此用系统特征值实部和虚部的不确定性摄动来反映系统的建模误差。

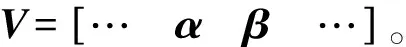
(13)

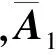
σi=σi0(1+WiσΔiσ)

(14)

ωi=ωi0(1+WiωΔiω)

(15)

式中,σi0和ωi0为标称值;Wiσ和Wiω分别为特征值实虚部的加权值;Δiσ和Δiω满足|Δiσ|≤1,|Δiω|≤1。将式(14)和式(15)代入式(13)中,引入反馈量zA,wA,可得:

(16)

(17)

对上式进行拉氏变换得颤振飞行试验中的广义系统算子P和不确定性算子Δ的关系为:

(18)

这样就得到考虑了动压摄动和特征值摄动的鲁棒气动弹性系统模型,式(18)可由图2所示的框图表示。

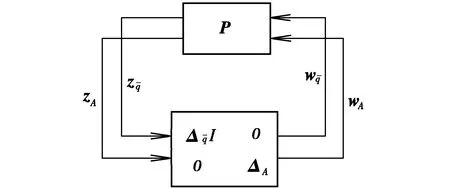
图2 试飞气动弹性鲁棒系统框图Fig.2 Aeroelastic robust system block diagram of flight test

3.3 模态特征值实虚部摄动量的估计

通过飞行试验测得第i阶模态的频率和阻尼比的n组值ωik和ζik(k=1,2,…,n),进行以下统计分析:

(19)

模态频率和阻尼比的摄动量为:

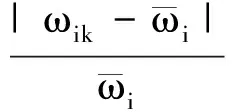
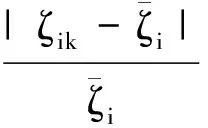
(20)

根据特征值实虚部与模态频率及阻尼比的关系,可得第i阶系统特征值虚部的摄动量即为Wiω,实部摄动量为Wiσ=Wiω+Wiζ。

3.4 颤振裕度与颤振边界预测

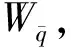
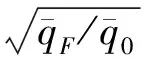
(20)

4 计算结果及分析

以海高0 km作为计算参考高度,首先计算标称颤振边界。图3为V=400 m/s飞行状态计算的标称μ曲线,颤振边界Vf=490 m/s,曲线峰值对应频率f=16.6 Hz。其次计算鲁棒颤振边界,假定根据试飞数据得到的模态频率和阻尼摄动量分别为5%和15%。图4为V=400 m/s飞行状态计算的鲁棒μ曲线,颤振边界Vf=454 m/s,曲线峰值对应频率f=16.6 Hz。由于引入了系统参数摄动,μ曲线不再光滑,得到的颤振边界趋于保守。

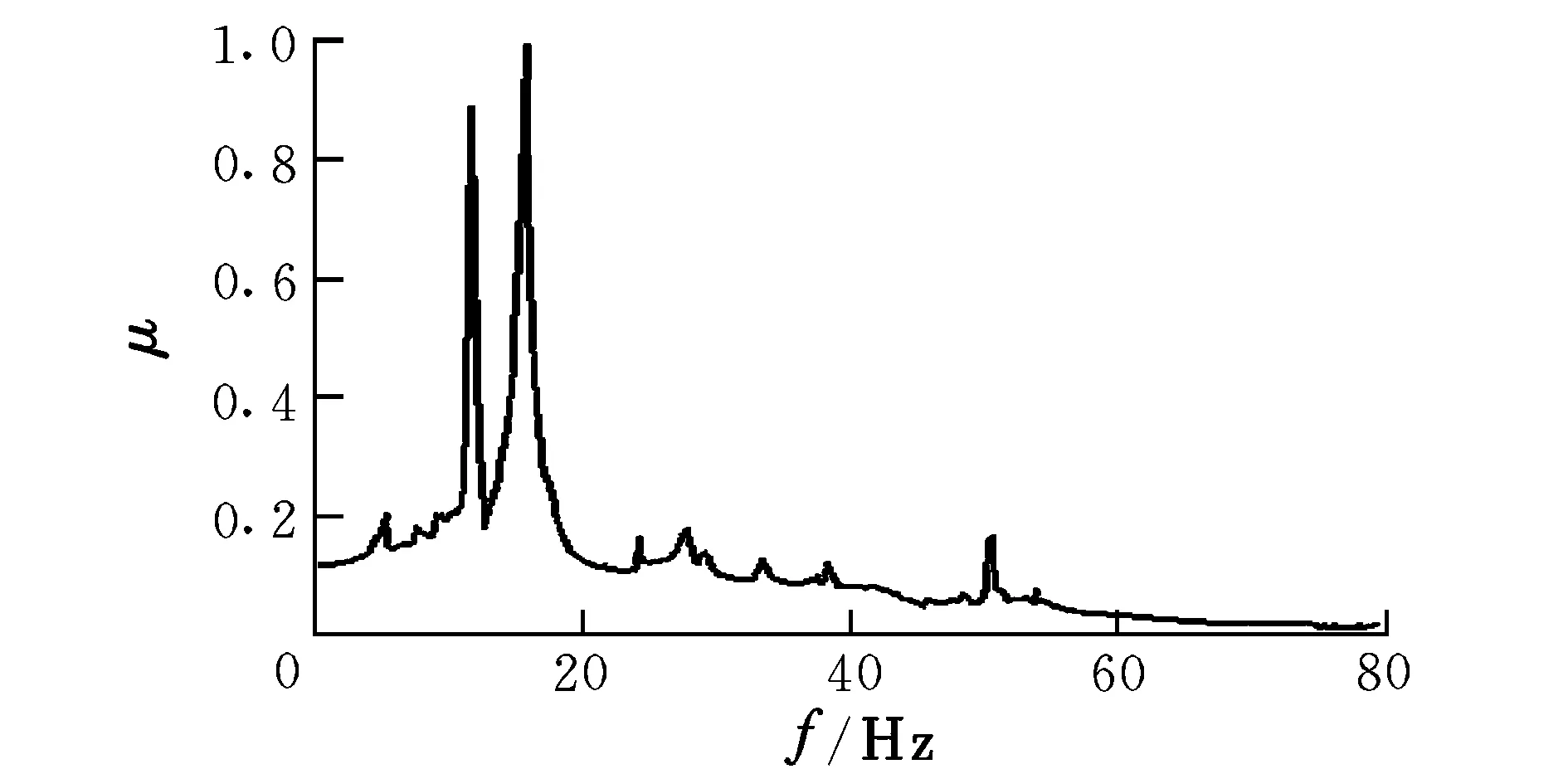
图3 对应标称颤振边界求解的μ曲线Fig.3 μ curve corresponding to the nominal flutter boundary

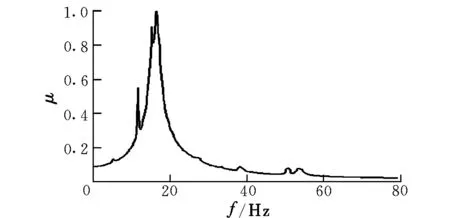
图4 对应鲁棒颤振边界求解的μ曲线Fig.4 μ curve corresponding to the robust flutter boundary

表1是几种方法得到的颤振边界结果。由表中数据可知,随状态点速度增大,标称系统得到的颤振边界趋于稳定并与p-k法得到的颤振边界一致;而计算得到的鲁棒颤振边界也趋于稳定,但明显小于标称颤振边界。

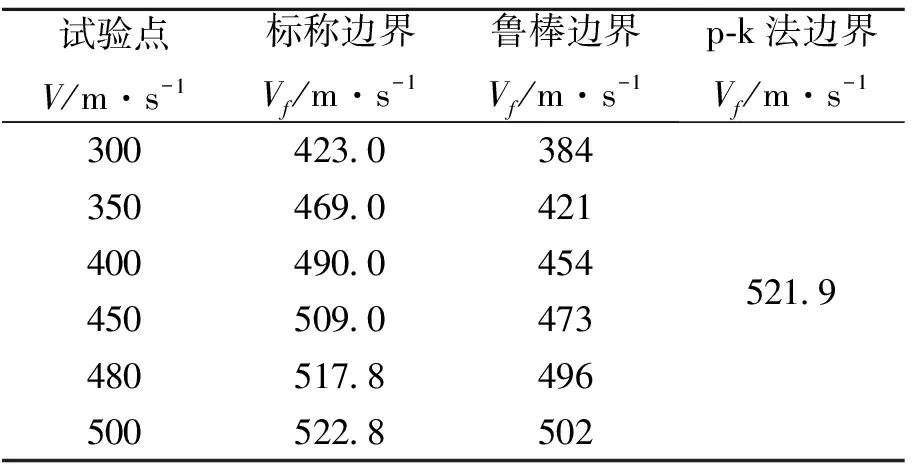
表1 海平面高度标称颤振边界预测与鲁棒颤振边界预测比较 Table 1 Sea level nominal flutter boundary compared with robust flutter boundary

5 结束语

鲁棒颤振裕度分析方法克服了传统的理论设计分析方法和飞行试验方法无法考虑误差的缺点,使得二者数据资源共享。在飞行试验过程中,根据安全飞行状态下的飞行数据确定模型误差的大小,通过计算鲁棒颤振裕度可以指明下一试验的安全测试点。这种方法与阻尼参数识别及外推不可靠时的情况相比,飞行试验状态点以及所需要的飞行时间明显减少,否则需要在试飞过程中慢慢扩展飞行包线。现代飞机具有自动控制系统,飞机结构与控制系统耦合产生了气动伺服颤振问题,本文讨论的鲁棒稳定性μ分析方法也适用于飞机气动伺服弹性飞行试验,同样具有前述优点[7]。

[1] 中国人民解放军总装备部.GJB 67.7A-2008 军用飞机结构强度规范 第7部分:气动弹性[S].北京:总装备部军标出版发行部,2008.

[2] 管德.飞机气动弹性力学手册[M].北京:航空工业出版社,1994.

[3] Lind R,Brenner M.Robust flutter margin analysis that in-corporates flight data[R].NASA/TP-1998-206543,

1998.

[4] 魏巍.MATLAB控制工程工具箱技术手册[M].北京:国防工业出版社,2004.

[5] 黄琳.稳定性与鲁棒性的理论基础[M].北京:科学出版社,2003.

[6] 宋晨,杨超,吴志刚.3种气动弹性状态空间建模方法的对比[J].航空学报,2007,28(S):1621-1626.

[7] Lind R,Brenner M.Analyzing aeroservoelastic stability margins using theμmethod[R].AIAA-98-1895,1998.

Robuststabilityanalysisanditsapplicationinflightfluttertest

WANG Dong-sen1, WU Zhi-gang2, ZHOU You-ming1

(1.Aircraft Flight Test Technology Institute, CFTE, Xi’an 710089, China； 2.School of Aeronautic Science and Engineering, BUAA, Beijing 100191, China)

This article combined with the present domestic and foreign research situation and the engineering application demands, combining the theoretical design model data and the flight measured data and using the structured singular valueμanalysis method based on the control theory, the flutter boundary can be predicted in flight test process, directly get conservative critical flutter dynamic pressure or flutter critical speed, which can increase the test security, shortening the flight test time, reduce test points and save test cost, it is a beneficial supplement of the currently flutter flight test method.

flutter; robust stability; structured singular value; flutter boundary

V217

A

1002-0853(2013)04-0372-04

2012-11-29;

2013-05-09; < class="emphasis_bold">网络出版时间

时间:2013-06-06 13:21

王东森(1972-)，男，陕西宝鸡人，高级工程师，硕士，研究方向为飞机颤振及振动试飞。

(编辑：方春玲)