一种改进的航路容量评估模型＊

张兆宁 王 霞 胡亚磊

（1.中国民航大学空中交通管理学院 天津 300300；2.中国联合航空有限公司 北京 100076）

0 引言

近年来，我国航空运输业的迅速发展，空中交通流量的急剧增加导致了空中交通网络的拥挤，飞行冲突和航班延误问题日益严重。航路，作为目前国内空域结构的基本组成单元，其容量评估的准确性将直接影响到流量管理实施的效果。航路容量是指在给定时间内，对于相对确定的高度层流量配置和机型配置，航路所能容纳的最大航空器架次。［1］在影响航路容量的诸多因素中，军事活动因素对航路容量产生了很大的影响。［2］而国内在这方面的研究还仅仅处于概念了解和定性分析阶段［3－6］，实际空管运行中也是采取粗放的隔离措施，造成了空域资源的浪费。所以，在航路最大容量的基础之上，研究加入军事活动因素的影响，对航路容量进行动态评估，可以为有效促进航空运输飞行安全、流畅运行提供保障。

1 航路最大容量计算模型

国外学者Janic［1］在考虑空域结构、交通流特征和管制规则等因素的基础上，初步实现了航路的容量估计。忽略备用高度层数量，以及主用高度层和备用高度层上航空器比例的影响，假设各个高度层都处于饱和状态，航路中飞行的航空器不允许超越，不考虑航路交叉点的影响，航路最大容量模型如下。

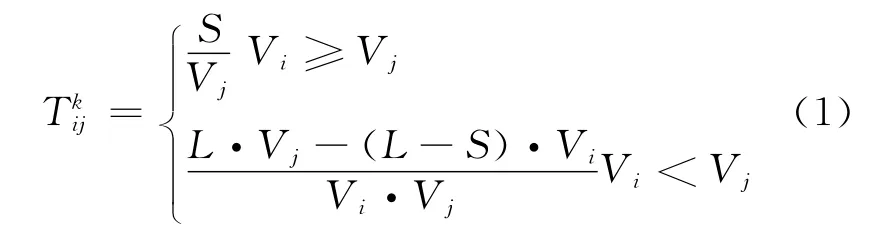
平均的时间间隔

第K 高度层的容量

航路总容量

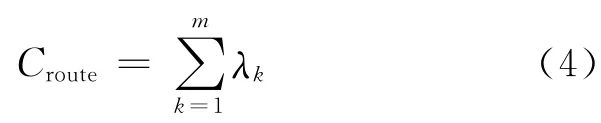
以上模型计算出的航路容量仅表明了理想情况下航路段所能容纳的最大航空器架次，而在实际运行中，航路受诸多可变因素影响，实际服务架次往往无法达到航路段的理论容量。在影响航路容量的诸多因素中，军事活动对航路容量的影响较为明显。

2 军事活动因素分析

由于军事活动影响，以上航路最大容量模型中各参数会发生相应的变化，本文重点讨论参数的选取。

多年来，民航空域中很少设有军航固定穿越地段，军航飞行可以随时、随地、随高度穿越航路航线。目前我国军、民航飞行间隔标准不同，如军航在高空飞行仍要求有1 000m的垂直间隔，而非民航所规定的600m 垂直间隔（6 000～12 000 m 空域）。以军航歼七常用的8 000m 高度为例，民航需空出7 200m、7 800m、8 400m3个高度层。一批次几架歼七编队飞行需要几万甚至上十万平方公里的范围让出上下2 000m的空域。［9］

炮射影响空域主要集中在靶场附近，人工降雨炮点，对空射击海域等。2005年以来，军航和工业部门对空发射任务迅速增多，由于任务特殊、飞行调配余地小，炮射活动一般都有固定的时限限制，造成航路无法使用。在避让方面，发射单位强调，发射任务特殊，一旦准备好，发射时间很难改变，加之现行避让规定中对发射任务没有规范，因此在避让原则问题上很难达成一致。在净空方面，有时首区、落区和飞行轨迹下方都净空；有时只首区、落区净空。首区、落区净空时，有时距离首区、落区较近的空域和航路、航线也要净空。［10］

为了便于分析军事活动对航路容量的影响，主要考虑以下4种情况：

情况1。军航飞机加入航路飞行。

情况2。军航飞行占用航路高度层。

情况3。军航飞行穿越航路。

情况4。军事炮射活动占用某一块空域。

3 航路动态模型的建立

情况1。当军航飞机加入航路飞行，但是遵循军航的纵向飞行间隔M，那么航路容量就有可能发生变化。当M＝S 时，航路的容量保持不变。

当M≠S 时，

此时K 高度层的容量为

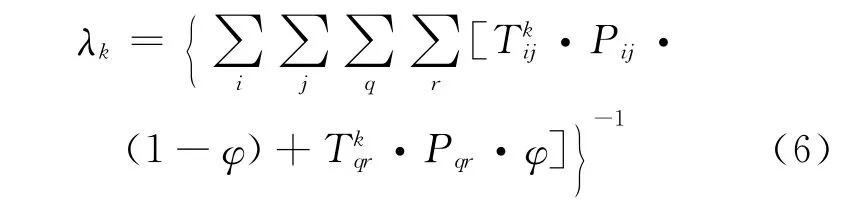
航路总容量

式中：q、r为航路上军用航空的种类；Vr为第r 类飞机在K 高度层的飞行速度；Tkqr为军机组合（q，r）达到军航最小飞行间隔M 时对应的时间间隔；Vq、Vr分别表示第q，r类飞机在K 高度层的飞行速度；Pq、Pr分别表示K 高度层上q、r类飞机所占的比例；φ为K 高度层军用航空器总的比例。

情况2。假设军航飞行只占用航路e个高度层（e≤m），其余高度层均为民航机飞行。则有以下结论。

有军用航空器飞行的K 高度层的容量同式（6）。

只有民航机飞行的L 高度层的容量为

航路总容量

情况3。当有军航飞行穿越航路时，假设穿越航路的时间段为t1（军航飞行首机和尾机安全飞行所需的时间间隔均包括在内），则在时间段t1内，民航的飞机均禁止通行。设影响的高度层为e个（e≤m），则有如下公式：

K 高度层的容量为

航路总容量为

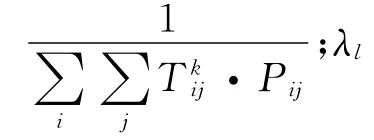
情况4。军事炮射活动占用某一块空域。在航路最大容量的基础上，通过分析影响因素影响系数，与最大容量相乘得到相应容量值为

则航路容量为

4 安全间隔计算

如果考虑军事活动占用航路的随机属性，并假设其服从正态分布；为了确保不以高于qc的概率违反空管最小间隔的规定，管制员一般需要在间隔规定之外加入额外的缓冲时间，见图1。

图1 相继到达飞机对的缓冲时间示例图Fig.1 The diagram of a pair of arriving aircrafts on the buffer time

假设：

1）军事活动占用航路的时间为T，且T～N（μt，σt）。

2）相继到达航路入口点的飞机对（i，j）之间的时间间隔为Rij，则有Rij－T≥0

计算安全概率（航路容量为C′route的概率）为

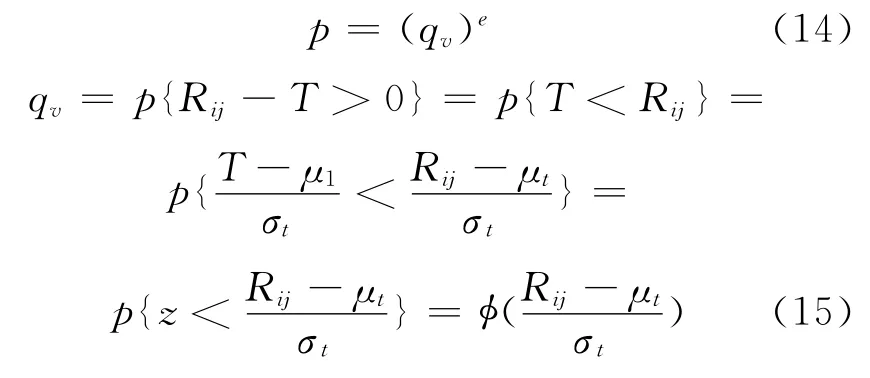
取其逆函数

则航空器相继到达航路入口点的飞机对之间的时间间隔应为：

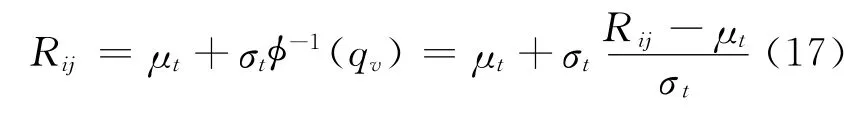
5 算例分析

以某航路为例，按照表1中的试验参数设置各种机型的比例、飞机架次和管制间隔进行算法试验，其中飞机架次和各机型比例参数主要用来产生1个随机的仿真飞机流，以此计算飞机在航路各高度层上飞行时的平均速度。

表1 算法试验参数表Tab.1 The form of algorithm parameters

根据文章第2部分设定的4种军事活动因素分别设置参数，作用于选定的航路，则该航路的实际容量发生变化，具体结果如下表所示。从算法试验结果可以看出：在单位时间内相同的仿真飞机流、相同起始点的航路段的容量随不同情况的军航活动因素影响而发生变化，多次试验结果表明，由该模型仿真计算得到的容量比较稳定，验证了该模型的可行性。

表2 算法试验结果Tab.2 The results of algorithm test

6 结束语

针对军事活动对空域容量的影响，考虑了4种影响航路容量的方式并进行了初步研究。建立了有军事活动影响下的航路容量评估模型，确定了军事活动影响航路容量的各个参数，推导出了相继到达航路入口点的飞机对之间的安全时间间隔，使容量评估结果具有相应的置信度。通过实例对航路容量进行了评估计算，得到了有军航活动影响时的航路容量，与实际情况基本符合。为评估有军事活动影响下的航路最大容量提供了理论依据。

模型中没有考虑随机性等其它不确定性因素对航路容量的影响，可在本文基础上深入研究，获得更精确的评估结果。

［1］Janic M，Tosic V.Enroute sector capacity model［J］.Transportation Science，1991，25（4）：215－224.

［2］窦 荣，胡明华.王艳军.基于飞行需求的航路动态管理［J］.航空计算技术，2008，38（6）：25－31.

［3］余 静，刘 洪.一种改进的航路动态容量计算模型［J］.四川大学学报，2007，44（5）：1005－1008.

［4］余 静，杨红雨，马博敏，等.证据理论在机场动态容量预测模型中的研究［J］.电子科技大学学报，2010，39（1）：141－144.

［5］中国民用航空局.2010 年民航行业发展统计公报［R］.北京：中国民用航空局，2011.

［6］王艳军.区域空中交通容量动态评估研究［D］.南京：南京航空航天大学，2007.

［7］Tofukuji.An airspace design and evaluation of en－route sector by air traffic control simulation experiments［J］.Electronics and Communications in Japan，Part 1（Communications），1996，79（8）：115－118.

［8］Zou J，Krozel J W，Krozel J，et al.Two methods for computing directional capacity given convective weather constraints［C］∥Proceedings of AIAA Guidance，Navigation，and Control Conference.Chicago：American Institute of Aeronautics and Astronautics，2009：1－15.

［9］吕人力.空域管理中的军、民航协商机制［J］.民航经济与技术，1997，184（4）：22－25.

［10］刘天成.关于缓解兰州管制区军民航飞行矛盾的思考［J］.空中交通管理，2007，35（8）：8－10.