基于神经网络的公路边坡稳定性实时判断＊

王树威 陈艳艳 陈 宁 赖见辉 吴克寒

（北京工业大学交通工程重点实验室 北京 100124）

0 引言

公路边坡稳定性实时预警是保障公路安全的重大关键问题之一。公路边坡稳定性安全系数Fs是衡量边坡稳定性的可靠指标，采用极限平衡理论计算Fs，并以此为依据进行公路边坡稳定的判断是1个可靠的方法，而且相关规范和文献中关于Fs的分级界定明确，可以避免人为设定变形值阈值引起的干扰，该方法已在公路边坡稳定性静态评价中得到了广泛的应用［1－3］。但Fs的计算需要岩土体的物理力学指标，而其中一些参数是不能实时获取的，导致不能通过直接计算Fs实现公路边坡稳定性的实时预警。

目前边坡工程的稳定性实时评价，采用监测变形值进行公路边坡失稳预警，如意大利Tele－Rilevamento Europa公司建立的永久散射体干涉合成孔径雷达边坡变形监测系统，通过对位移、裂缝等变形值的监测进行了Assisi滑坡的实时评价监测［4］；澳大利亚的Sirovision摄影测量与岩体结构分析系统对公路边坡进行连续摄影并分析比较相邻时段形变情况后，实现了边坡的稳定性实时评价［5］；美国Geokon Inc.的光纤光栅型位移监测系统采用实时监测位移值的方法，对公路桥梁、水利大坝、建筑结构等工程进行了安全监测［6］。上述监测系统通过实时监测到的变形值与预定变形阈值的对比分析，实现边坡失稳的实时预警。采用监测公路边坡变形值进行公路边坡失稳预警存在的最大问题为：因边坡稳定性与多个变形值相关，而各变形值的预警阈值受地质条件、水文条件、自然环境等多方面因素的影响，且阈值的设定与工程技术人员的经验密切相关，所以实时预警的效果易受人为因素的影响。

针对上述问题，本文采用极限平衡理论进行公路边坡的稳定性安全系数Fs计算，同时进行公路边坡的变形值（位移值、裂缝值、倾斜度）监测，采用神经网络方法建立Fs与变形值的关系模型，该模型可以通过实时监测的变形值直接计算输出Fs，从而实现通过Fs进行无粘性土公路边坡稳定性的实时预警，最后通过对某无粘性土公路边坡的实验证明了模型和方法的有效性。

建立Fs和变形值的关系表达式如下：

式中：p1为公路边坡位移监测值；p2为公路边坡裂缝监测值；p3为公路边坡倾斜度监测值。

显然，如果能得到上述函数关系，则通过实时监测位移值p1、裂缝值p2、倾斜度p3即可得出实时的公路边坡稳定性安全系数，从而实现采用Fs值进行边坡失稳预警的目的。

1 稳定性安全系数计算

公路边坡稳定性安全系数Fs通常采用极限平衡理论进行求解。以降雨诱发的覆盖层公路边坡平面型滑坡为例，其地质条件是上面是残坡积物或风化层，透水性较大，下为基岩透水性较小，破坏面常为两者的接触面。它类似于平面滑裂面滑坡。以Iverson［7］的解析解来描述降雨入渗引起的暂态渗流场，采用极限平衡理论中的Mohr－Coulomb强度理论和相适应的流动法则［8－9］对降雨诱发的平面型滑坡前的公路边坡坡体进行弹塑性分析，其力学计算分析简图见图1。

图1 力学分析简图Fig.1 Mechanical analysis diagram

同时，对其进行如下假定。

1）不透水面和初始地下水位分别在地面下深度为d和dw处，且都平行于坡面。

2）拟滑土体均匀且各向同性，为弹性－理想塑性材料，屈服服从Mohr－Coulomb准则，并遵循相适应的流动法则。

3）地下水的补给仅由降雨补给，不考虑蒸发等损失，且地下水位以上的土体也完全饱和，即整个拟滑土体具有相同的重度γsat。

4）不计降雨前土体下部因可能存在塑性区而具有的初始塑性应变，初始时假定平行于坡面的初始有效应力σ′x0正比于垂直于坡面的初始有效应力σ′y0，即

式中：k0为土的侧压力系数。

对于弹性材料，k0与泊松比μ的关系如下。

为简便起见，设降雨强度I在整个降雨期间T 内为不变。根据Iverson可得时刻t深度Y的孔隙水压头为

式中：K为饱和渗透系数；H（η）为Heavyside阶梯函数；α为坡脚；D0为饱和水力扩散系数，D1可由式（5）计算得到。

函数ierfc（η）定义如下。

式中：erfc（η）为互补误差函数。

另外，式（4）中求得的孔隙水压头φ（Y，t）应满足下式

这样，时刻t深度Y的稳定性安全系数计算如下。

式中：c′为土体的有效粘聚力；φ′为土体的有效内摩擦角；γw为地下水的重度。

式（8）中计算得到的最小值即为时刻t边坡的稳定性安全系数。

2 神经网络

公路边坡稳定性安全系数Fs与变形值的关系复杂，同时，神经网络可通过参数化逼近的方式获取非线性函数关系，并在非线性系统建模领域中得到了广泛的应用。所以，这里采用LM 神经网络建立Fs与边坡变形值的关系模型。神经网络学习的目的是通过改变各神经元的连接权值实现在给定输入xp下神经网络的输出yp与相应输入下样本的输出dp尽可能地接近，即神经网络的实际输出尽可能地接近期望输出。相对于本文，给定的一组样本［（x1，d1），（x2，d2），…，（xP，dP）］。式中：x为样本输入，即实时监测到的公路边坡变形值；d为给定输入下期望的样本输出，即1组变形值所对应的Fs；P为学习样本个数。

神经网络的结构见图2。

公路边坡稳定性安全系数Fs的每个神经元，输入值取公路边坡变形值（位移值、裂缝值、倾斜度）作为输入，输入维数为3，即x＝［P1，P2，P3］T；隐含层神经元输出为ho，其中，ho＝［ho1，ho2，ho3］T，隐含层神经元个数为3，隐含层神经元的输入为hi，其中，hi＝［hi1，hi2，hi3］T；Fs为输出层神经元的输出，记为y＝［y1，y2，…，yM］T，其中，M为输出神经元个数。输出模型如下。

图2 神经网络结构图Fig.2 The structure diagram of modular neural network

式中：y为公路边坡稳定性安全系数；wi为第i 种变形值所对应的权重系数；xi为第i 种公路边坡变形值。

BP算法的训练一般采用误差反向传播的梯度下降算法，这种算法在参数接近最优值附近时收敛速度较慢，为避免这个问题，这里采用Levenberg－Marquardt（LM）算法对神经网络的权值进行学习，LM 算法的优点在于网络权值数目较少时收敛非常迅速，并且可以获得较高的精确度［10－11］。LM 算法的基本原理：设定变量w 代入神经网络模型f（x，w），对模型进行不断的调整使得期望的Fs样本d与输出的Fs样本y的偏差平方和S（w）最小，即：

如同其他的极小化求解方法，LM 算法同样为1个重复迭代求解的过程，解题建模过程为：

第二，中华民族的百年复兴，绝非一帆风顺之事。随着13亿人民的脱贫致富，各种不适应、不甘心、不服气，会接踵而来。在敞开国门、融入全球化的同时，一定不要忘了首先把自己的事情做好，打铁先要本身硬，年轻一代，任重道远。

1）假定1 个参数变量w0，代入公路边坡变形值x求解得到偏差平方和S（w0）值。

2）取极小值δ得到参数变量w－1如下，即w1＝w0＋δ，代入得到函数f（xi，w1），使其满足线性化要求；

3）当偏差平方和S（w1）取得最小值，且S（w1）的值并不随着δ的取值而发生变化时，此时偏差平方和S（w1）如式（12）所示。

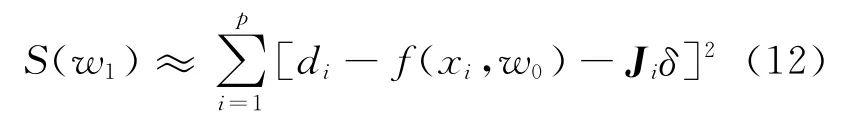
上式可采用向量形式表达，如式（13）所示。

4）偏差平方和S（w1）足够小时，可近似取值为零，得到式（14），并由此计算得到δ值。

5）引入非负参数λ和单位矩阵I，得到计算式（15），迭代过程中进行参数λ的调整，并采用高斯牛顿运算法则进行计算，直到计算得到的偏差平方和S（w）达到预先设定值，迭代停止，此时的w 值即为所求权重值。

3 模型试验测试

本文选用的力学计算参数和变形值数据为某城市道路K1＋280～K1＋320段西侧边坡，边坡坡角α＝20°，土体厚度d为1～4m，初始地下水位距地面深度dw为1～4m，K为渗透系数，且其取值I／K＝0.012，0.025，0.05，0.1，0.3 分别对应着小雨、中雨、大雨、暴雨、大暴雨的上限。同时，边坡共设立了6个变形监测点，某时间段内的边坡变形值以6个监测点中的最大值为准，监测时间为2010年2月22日至8月31日。

通过上述计算，得到公路边坡稳定性安全系数Fs与变形值的关系曲线如图3所示。

图3 边坡稳定性安全系数与变形值关系曲线Fig.3 The curve between safety factor of slope stability and deformation value

通过对公路边坡实时变形值分析得，此公路边坡的失稳表现为水平向外、竖直向下的破坏形式，且Fs值不断的降低，与公路边坡的实际情况相符，Fs值与变形值存在一定的关系，随着变形值增大而降低，但是降低的幅度慢慢的降低。

取2010年2月22日至7月31日的监测数据用于网络训练，2010年7月1日 至8月31日的监测数据用于模型的测试。按照时间顺序进行数据编号，稳定性安全系数Fs计算值及采用神经网络模型得到的稳定性安全系数Fs见图4。

图4 神经网络模型测试曲线Fig.4 The curves of modular neural network model

模型输出值和实际值的相对误差曲线见图5。

图5 神经网络模型测试误差曲线Fig.5 The test error curves of modular neural network model

将分析得到的神经网络模型、马崇武模型［12］和实际值进行误差比较，见表1。

进一步计算得到，由神经网络得到的公路边坡稳定性安全系数计算模型与实际值的误差为马崇武经验模型的29%～75%，模型精度有所提高。

表1 边坡稳定安全系数与实际值对比表Tab.1 Slope stability safety factor and the actual value comparison table

4 实例分析

由公路路基设计规范（JTGD30—2004）规定及公路边坡的具体适用条件，选此公路边坡稳定性安全系数Fs的失稳阈值为1.10，按照最不利原则在之后的监测中共出现3次失稳预警，见表2。

表2 监测结果统计表Tab.2 Statistics of monitoring results

从表2和实际监测知：①9月26日的6个测点的变形值如表所示，公路边坡处于基本安全状态，整体变化较小，仅坡脚有松动的迹象；②10月16日，公路边坡和建筑物存在一定的变形，公路边坡处于欠安全状态；③10月25日，且现场踏勘发现公路边坡处于不安全状态，边坡原有裂缝有所发展，局部发生滑塌破坏，施工支护体有外鼓、开裂的现象。

经工程实际应用检验后知，基于神经网络的公路边坡稳定性安全系数Fs和变形值模型能够满足工程所需，实现了公路边坡稳定性的实时监测判断。

5 结论

1）采用神经网络中的LM 算法建立了无粘性土公路边坡稳定安全系数Fs与变形值的模型，符合无粘性土公路边坡岩土体的特性，弥补和改善了确定性方法在无粘性土公路边坡实时稳定性判断中的不足，给出了无粘性土公路边坡实时稳定性判断的依据。

2）基于神经网络建立的无粘性土公路边坡稳定安全系数Fs与变形值的的关系模型，与其它模型曲线相比，精度有较大提高。

3）由于神经网络本身的学习能力和数据驱动特性，使模型具有较强的环境适应能力。随着样本的增多，可以采用定期重新学习的方式，进一步提高模型对变化环境的适应能力，从而扩大模型的实用范围。

［1］王庚荪.边坡的渐进破坏及稳定性分析［J］.岩石力学与工程学报，2000，19（1）：29－33.

［2］Cheng Y M，Lansivaara T，Wei W B.Two－dimensional slope stability analysis by limit equilibrium and strength reduction methods［J］.Computers and Geotechnics，2007（34）：137－150.

［3］Oztekin B，Topal T，Kolat C.Assessment of degradation and stability of a cut slope in limestone，Ankara－Turkey［J］.Engineering Geology，2006（84）：12－30.

［4］吕乐婷.重庆地区地表形变D－InSAR检测应用研究［D］.长春：吉林大学，2009.

［5］李焕强.台风暴雨引发公路水毁特征与边坡水毁机理［D］.杭州：浙江大学，2008.

［6］徐文杰，岳中琦，胡瑞林.基于数字图像的土、岩和混凝土内部结构定量分析和力学数值计算的研究进展［J］.工程地质学报，2007（3）：289－313.

［7］Iverson R M.Landslide triggering by rain infiltration［J］.Water Resources Research，2000，36（7）：1897－1910.

［8］陈祖煜.土质边坡稳定分析：原理·方法·程序［M］.北京：中国水利水电出版社，2003.

［9］Urciuoli G.Strains preceding failure in infinite slope［J］.International Journal of Geomechanics，2002，2（1）：93－112.

［10］Ranganathan A.The Levenberg－Marquardt algorithm［J］.SIAM Journal of Applied Mathematics，2004，11（2）：431－441.

［11］余正红，李志博，尹朝庆.基于遗传神经网络的货运量预测的研究与实现［J］.交通与计算机，2006，24（5）：93－99.

［12］马崇武，刘忠玉，田 君.地下水位升高时黏性土无限边坡的水平位移［J］.岩土力学，2008，29（5）：1249－1253.