货币时间价值中数学工具的应用

张占军

一、货币时间价值的内涵

货币时间价值是指货币在周转使用中随着时间的推移而发生的价值增值。该价值增值的实质是由于货币作为一种特殊的稀缺性商品，投资者因让渡其使用权而索要的对机会成本的补偿和对承担风险的补偿。时间价值原理揭示了不同时间点的单位货币的价值不相等，所以，不同时点上的货币收支不宜直接比较，必须将它们转换到相同的时点上，才能进行大小的比较和有关的计算。

二、货币时间价值的基本要素

货币时间价值的衡量对象是货币活动，而货币活动的两种基本类型是复利和年金，在利息不断资本化的条件下，复利是货币时间价值计算的基础，也就是说复利是年金的计算基础。年金按其每次收付款项发生的时点不同，分为普通年金、先付年金、递延年金、永续年金等类型。所以货币时间价值计算的关键是正确判断货币活动的类型，只要判断准确就能计算出相应的时间价值。在货币时间价值的计算中，所涉及的要素主要有终值（F）、现值（P）、利率（i）、计息期数（n）。

三、货币时间价值中数学工具的应用

为了形象的描述不同时点上货币之间的等值换算关系，我们经常会利用数学辅助工具来计算相应的货币时间价值。主要的数学辅助工具有：升（降）幂法、补割（割补）法、分割法、三角形相似法等。

（一）升幂法

在普通年金终值、现值公式的推导过程中，巧妙使用了降幂法，使公式的推导清晰明了。以推导普通年金终值的公式为例，普通年金终值（FVAn）是指一定时期内每期期末等额收付款项的复利终值之和，如图所示。

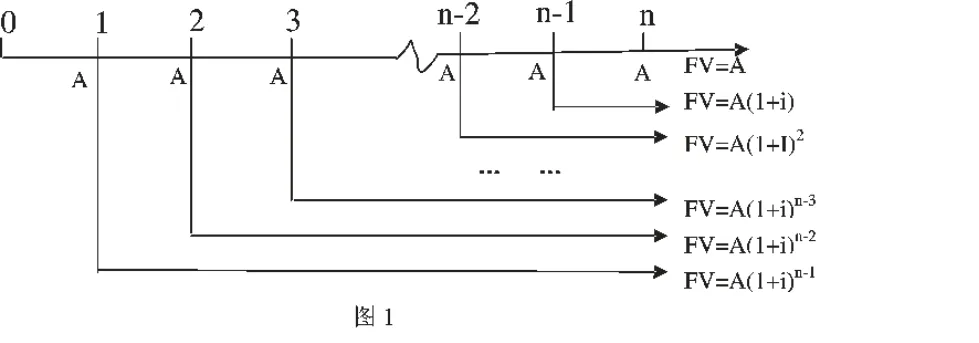
从图1 中可知：

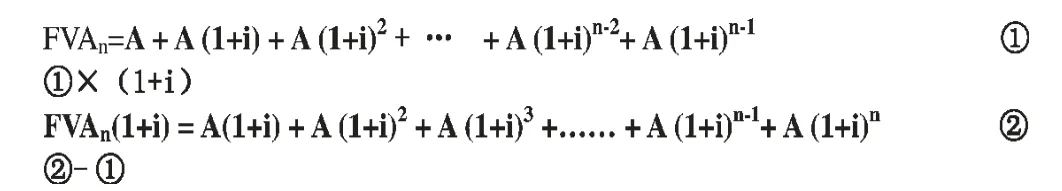
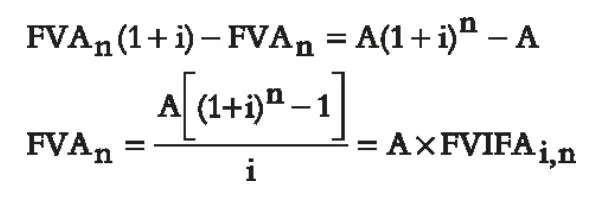
在普通年金现值公式的推导过程中也可以使用同样的方法。而在固定股利增长模型下的普通股资本成本的测算公式的推导可以用降幂的方法。

（二）补割（割补）法

在先付年金终值、现值公式的推导过程中，可以借用数学工具补割（割补）法可以形象的推导出其计算公式。以推导先付年金终值的计算公式为例。先付年金终值（XFVAn）是指一定时期内每期期初等额收付款项的复利终值之和。下例先付年金终值的计算公式既可以根据其含义用复利终值推导，又可以先把先付年金转换为后付年金，由后付年金来推导。下图是标准的先付年金，用转换方法推导其公式。

在图2 的基础上往前延长一年，把先付年金转换为后付年金转化成图3，再在图3 上第n+1年上补个A。则就变成了标准的后付年金终值的计算，在此基础上割去A 就推出了先付年金终值的计算公式，即：XFVAn=A×FVIFAi.n+1-A。先付年金现值可以用割补法来进行推导其计算公式，方法同理。

（三）分割法

还是以推导先付年金终值的计算公式为例，其原理是先把先付年金转换为后付年金，由后付年金来推导先付年金终值的计算公式。

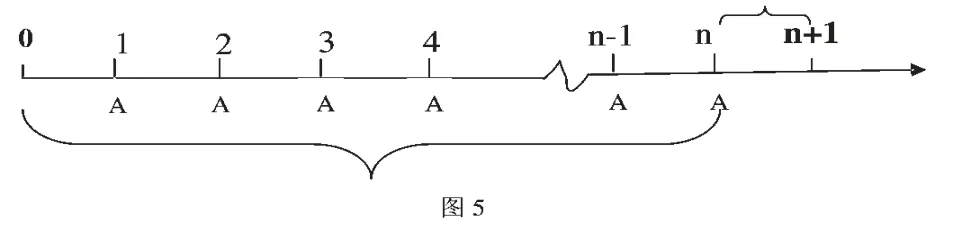
根据图3 分割后转化成图5，图5 前n年是一个标准的后付年金终值的计算，即FVAn=A×FVIFAi，n，这个值可以看作是第n+1年的复利现值，则就可以推导出先付年金终值XFVAn=A×FVIFAi，n×(1+i)。

（四）三角形相似法

三角形相似法主要用在货币时间价值要素中利率和期数计算，由于利率和期数包含在终值、现值系数中，所以只有计算出终值、现值系数的值才能通过系数表查出，查不出其值就只能用内插法来计算。以下以计算年金现值中的计息期数为例，原理是在其他要素不变的情况下，计息期数与现值系数成同方向变动的关系，利用这一关系构建相似三角形。

例：甲企业向银行贷款5000万元进行工程项目投资，假设银行借款利率为16%，该工程当年建成投产，投产后每年可获净利1500万元，全部用来归还贷款的本息，需要多少年才能还清？

解析：由PVIFA16%n=5000/1500=3.333。通过年金现值系数表，不能查到计息期数，此时只能用内插法找到3.333 的临界的两个现值系数值，及其对应的计息期数，然后根据三角形相似法求解。见下图。

临界值（5，3.685），（6，3.274）之间的弧线可以近似看作是直线，构建三角形△ABC∽△ADE，相似三角形对应变成比例。即

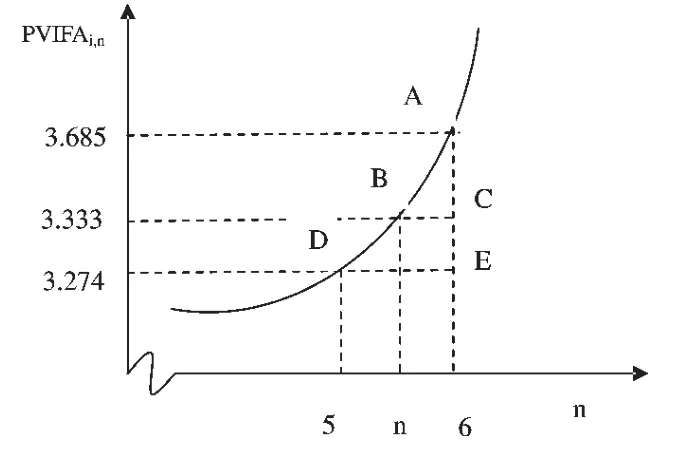
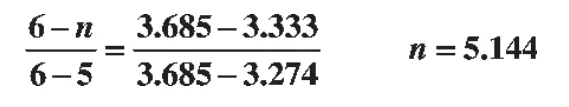
总之，财务管理中的定量分析很多，应该把数学的工具形象而巧妙的与之相结合。这样可以加深学生的理解，提高教学质量。

［1］荆新，王化成，刘俊彦.财务管理学【M】.北京：中国人民大学出版社，2012.

［2］郭巧丽,王彦东.《货币时间价值中插值图示法的运用》，《财会通讯》，2011年第4期.