供应链回购合同的权重效用利润函数分析
王军臣, 谢 燕
(南通大学 理学院, 江苏 南通 226007)
供应链回购合同的权重效用利润函数分析
王军臣, 谢 燕
(南通大学 理学院, 江苏 南通 226007)
引入供应链权重效用利润概念,研究在回购合同协调供应链前提下权重效用利润相对于传统效用利润能否增加的问题.在权重效用利润函数最大值问题的研究基础上,证明了可以通过修正相应的合同参数形成新的协调性回购合同使得利润增加,并给出相应的的合同条款并给出具体数值例子验证结论.
供应链; 供应链协调; 回购合同; 权重效用利润函数
0 引言
20世纪90年代,随着物流管理的逐步发展产生了供应链管理产业.由于供应链上下游企业成本结构的异质性,往往导致在供应链系统中出现“双重边际效应”,即供应链双方都有一定的市场力量,若两者缺乏协调的定价决策,就会导致最终价格高于使供应链总利润水平最大化时的价格,从而使得分散式供应链的效率很难达到集成式供应链的效率水平.因此,必须通过某种合同来使分散式的供应链双方达到协调运作目的.
本世纪初,对于由单一供应商和销售商构成的供应链性能的研究越来越多[1-2],尤其是对供应商和销售商能保证自己利益的前提下提高整个供应链性能的研究[3-4].2003年,Cachon[5]对协调供应链的合同给出了具体的特征描述:第一,该合同能够产生一族满足Nsah均衡的供应链优化决策;第二,该合同允许利润的任意分配;第三,该合同被双方接受.同时,Cachon 还充分证明了回购合同、数量弹性合同、数量折扣合同等是可以协调分散式供应链.2005年,Bernstein 和Federgruen提出了“完美协调机制”[6],指的是促使分散式供应链能像集成式供应链一样追求最大预期利润,但缺乏具体的解决方案.2010年,Behzad Hezarkhani和 Wieslaw Kubiak通过隐形价格机制提出供应链中关于双方运输的协调合同,但在价格制定等方面不够完善[7].2011年Jing Chen 和 Peter C. Bell 完善了两种回购价下合同的协调问题,但是需要另外安排供应链利润的分配[8].
本文在保证合同协调的前提条件下,对权重效用利润和传统效用利润进行分析比较.通过对最优订货量的确定来制定提高效用利润的新式合同.
1 权重效用利润函数

设当销售商的需求量达不到其订货量时,销售商赔付供应商的货物单价为gr,相反,若供应商无法提供给销售商足额的订货量,其赔付单价为gs.方便起见,记c=cs+cr,g=gr+gs.销售期结束后,供应商以单价v从销售商处回收剩余产品,要求v 基于上述给出的各个变量,我们得到销售商和供应商的利润函数分别为 πr(q)=pS(q)+vI(q)-grL(q)-crq-T (1) πs(q)=gsS(q)-csq-gsμ+T (2) 那么,供应链的利润函数为 π(q)=πr(q)+πs(q)=(p-v+g)S(q)-(c-v)q-gμ (3) 在供应链利润取得最优时,对应存在最优订货量.我们记q0为供应链最优订货量,即q0=argmaxπ(q).假设π(q0)>0,由于F是严格增函数,π是严格凹的且最优订货量是唯一的.进一步,q0满足: (4) 供应链的总利润π=πs+πr实际上就是建立在πs,πr两个目标上的一种特殊的效用函数,此时,供销双方的权重是相同的,我们称此时的供应链利润为传统效用利润, 对应的利润函数为传统效用利润函数. 由于市场供需情况的变化,决策者对商品的批发价格、销售价格、回购价格的决策时, 有时会考虑到供应双方利润追求在决策中的不同地位问题, 由此, 我们可以考虑权重效用利润函数.设λs,λr分别为供应商和销售商利润在决策中的权重,那么0≤λs≤1,0≤λr≤1,λs+λr=1,得到供应链权重效用利润函数[9]: π(λ)=λsπs+λrπr (5) 在回购合同中,记供应商对单位商品的报价为ω,在销售期结束后以单价b回购.然而,销售商剩余下来的这部分产品主要分为两种类型:一种是未销售完的剩余库存,另一种是消费者返还的不满意产品.2011年,Jing Chen 和 Peter C. Bell 考虑了当销售商面对顾客退货时的价格随机制定问题.在此问题中需要考虑顾客的返还率α以及销售商对顾客的赔偿价格r是如何协调供应链的,并且得到了下面相关结论. 定理1[8]在由销售商决定零售价格和销售数量的分散式供应链中,当价格基于市场需求的不确定性和顾客的返货率同销售量成比例时,实现供应链协调的条件为: 定理2[8]在给定销售商对顾客的赔偿价格r的情况下,随着顾客返货率α的增大,供应商必须相应提高产品批发价w和回购价v. 考虑到顾客退货的情况,销售期结束后的回购价b=rα+v(1-α),在现实意义下,销售商不可能从剩余库存中盈利,故b≤ω.则对应的预付款为 T(q,ω,b)=ωq-bI(q)=bS(q)+(ω-b)q (6) 同时,由(1)和(6)可得销售商的利润函数为 πr(q,ω,b)=(p-v+gr-b)S(q)-(ω-b+cr-v)q-grμ (7) 并且此时对于回购参数λ′≥0有 p-v+gr-b=λ′(p-v+g) (8) ω-b+cr-v=λ′(c-v) (9) 综合(7)、(8)和(3),得到 πr(q,ω,b)=λ′π(q)+μ(λ′g-gr) (10) 同样,供应商的利润可表示为 (11) 同时,比较(8)和(9)得到销售商的单位报价为 (12) 并且,对于λ′∈[0,1],该合同协调整个供应链. 在回购合同中,设供应商在供应链中的权重为λ,销售商的权重为1-λ.由此,根据(1)、(2)、(5)和(6),供应链的权重效用函数为 π(λ)=[λgs+(1-λ)(p-v+gr)+(2λ-1)b]S(q) -[λcs+(1-λ)(cr-v)-(2λ-1)(ω-b)]q-[λgs+(1-λ)gr]μ (13) 证明对于权重效用函数我们考虑回购合同中各个参数使得对于δ≥0: p-v+gr-b=δ[λ(p-v+g)+(1-2λ)(p-v+gr-b)] (14) ω-b+cr-v=δ[λ(c-v)+(1-2λ)(ω-b+cr-v)] (15) 由(14)和(15),此合同中销售商的利润函数可化为: πr=δ[λ(p-v+g)+(1-2λ)(p-v+gr-b)]S(q)- δ[λ(c-v)+(1-2λ)(ω-b+cr-v)]q-grμ= δπ(λ)+δ[λgs+(1-λ)gr]μ-grμ (16) (17) 分别对销售商和供应链权重效用函数求导数,我们有 对应的批发价为 显然,两种情况下上与(12)是等价的. (18) 由(12),(18)可化为 那么,在保证供应链协调的情况下,φ是可以取得极值的.为了确定φ取得最值的具体情况,考察其二阶导数: φ=[gs+b-(p-v+gr-b)]S(q)+(2ω-2b+cr-cs-v)q+(gr-gs)μ= (1-2λ′)(p-v+g)S(q)-(1-2λ′)(c-v)q+(1-2λ′)gμ= (1-2λ′)[(p-v+g)S(q)-(c-v)q-gμ], (19) 由以上分析,我们得到以下结论. 定理5 在确定新的意义下的合同时,回购合同对整个供应链的协调性是不变的. 定理6 回购合同中,在给定了对顾客赔偿价格r的情况下,通过提高产品满意度(即减小α)可以降低产品出厂价ω和回购价格b实现权重效用利润相对于传统效用利润的增加. 现在,我们给出简单的例子来验证本文相关结论. 假设市场需求分布函数为: 则 令r=6,cs=3.5,cr=0.5,gs=0.6,gr=0.4,θ=1000. 表1 不同的退货率情形下供应链权重效用利润与传统效用利润对比结果 如表1所示,当顾客的退货率一定时,我们可以得到新合同的各个参数值,并且此合同既能协调整个供应链又能保证权重效用利润最大.同时,权重效用利润相对于传统效用利润是增加的.此外,随着顾客退货率的上升,通过供应商提高批发价,销售商降低零售价并降低订货量的方式来确保上述性质不变.此合同中各个参数满足任意数值例子,所以我们可以通过此方法对合同进行改进得到既能协调供应链又能提高效用利润的合同. 此方法为我们提供了一个优化供应链效用利润的一个思路.当决策者在对整个供应链进行决策时,通过对权重效用利润的分析得到合同中不同参数所需要满足的条件,这样做即可以保证合同对供应链协调的不变性,又可以使得供应链权重效用利润相对于特殊效用利润是增加的.需要进一步研究的问题是,对于建立在供应商和销售商利润上的一般意义下的效用利润函数,如何通过修正合同中的有关参数使得效用利润较之传统效用利润增加;其次,给出一般意义下效用利润增值的实际市场背景并如何以此指导市场. 致谢: 作者感谢本文指导老师淮阴师范学院秦志林教授的热心指导和帮助! [1] Donohue K L. Efficient supply contracts for fashion goods with forecast updating and two production modes[J]. Management Science, 2000, 46(11): 1397-1411. [2] Corbett J C, DeCroix G A. Shared-savings contracts for indirect materials in supply chains: Channel profits and environmental impacts[J]. Management Science, 2001, 47(7): 881-893. [3] Lariviere M A. Supply chain contracting and coordination with stochastic demand[M]. //Boston: Kluwer Academic Publishers, 1999. 233-268. [4] Taylor T. Supply chain coordination under channel rebates with sales effort effects[J]. Management Science, 2002, 48(8): 992-1007. [5] Cachon G P. Supply chain coordination with contracts[M]. //Amsterdam: North-Holland Press, 2003. 227-339. [6] Bernstein F, Federgruen A. Decentralized supply chains with competing retailer under demand uncertainty[J]. Management Science, 2005, 51(3): 409-426. [7] Behzad Hezarkhani, Wieslaw Kubiak. A coordinating contract for transshipment in a two-company supply chain[J]. European Journal of Operational Research, 2010, 207(1): 232-237. [8] Jing Chen, Peter C. Bell. Coordinating a decentralized supply chain with customer returns and price-dependent stochastic demand using a buyback policy[J]. European Journal of Operational Research, 2011, 212(2): 293-300. [9] 王文秋, 秦至林. 多目标规划问题的棱锥有效解[J]. 南通大学学报: 自然科学版, 2011, 10(2): 79-84. AnalysisontheWeightedUtilityProfitFunctionofBuy-BackContractinSupplyChain WANG Jun-chen, XIE Yan (School of Sciences of Nantong University, Nantong Jiangsu 226007, China) In this paper,the concept of weighted utility profit in supply chain was introduced, and the problem whether the weighted utility profit increase or not relative to traditional profit of buy-back contract was studied in the premise the contract coordinating supply chain. On the basement of research on the maximization of weighted profit utility function, a new buy-back contract was formed which not only coordinating supply chain but also increasing profit by modifying relative parameters in supply chain. Lastly, a numerical example was performed to support above conclusion. supply chain; supply chain coordination; buy-back contracts; weight utility function 2012-12-13 教育部人文社会科学研究规划项目(10YJC630213) 王军臣(1988-), 男, 河南焦作人, 硕士研究生, 研究方向为运筹学与控制论. O211.6 A 1671-6876(2013)01-0025-05 [责任编辑李春红]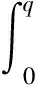
2 回购合同


3 回购合同中的权重效用函数

4 权重效用函数的极值分析
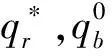




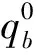
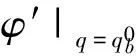

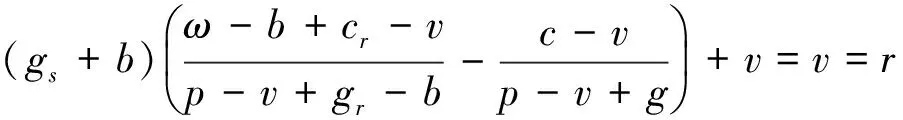
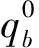





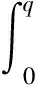
5 数值例子

6 总结

