广义集值变分不等式与互补问题的误差界
李 丽, 周厚春
(1.临沂大学 理学院, 山东 临沂 276005; 2.山东师范大学 数学科学学院, 山东 济南 250014)
广义集值变分不等式与互补问题的误差界
李 丽1,2, 周厚春1
(1.临沂大学 理学院, 山东 临沂 276005; 2.山东师范大学 数学科学学院, 山东 济南 250014)
引入了广义变分不等式的投影残量, 利用投影残量, 我们给出了集值映射为γ-严格单调(γ-一致P-映射)和 Hølder连续的广义集值变分不等式(广义集值非线性互补问题)的误差界,以上结论推广了一般的广义变分不等式(广义非线性互补问题)的相关结论.
集值映射; 广义变分不等式; 广义非线性互补问题; 误差界
0 引言
设F(x):C→2Rn为连续且具有非空紧值的集值映射,其中C是Rn上的非空闭凸集.广义集值变分不等式问题,记为GVI,就是求x*∈C,ξ1∈F(x*)使得
〈ξ1,y-x*〉≥0,∀y∈C
(1)

x*≥0,ξ1≥0, 〈x*,ξ1〉=0
(2)
广义变分不等式最早由Noor[1]提出,从误差界的角度,已取得很多重要成果[2-4].误差界是对任意一点到变分不等式解集合的距离估计,它在变分不等式的算法收敛性分析中起着重要作用[5-7].最近方长杰在文[8]中研究了广义集值变分不等式的误差界,在集值映射是Lipschitz连续和强单调的条件下,建立了误差界.本文在文 [8]的基础上对F是γ-严格单调(γ-一致P-映射)和Hølder连续的问题(1)(问题(2))的误差界进行研究.
1 预备知识
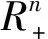
定义1 设集值映射F(x):C→2Rn,
(i) 称F在C上是Hølder连续,如果存在常数m>0,μ∈(0,1],对任意x,y∈C有H(F(x),F(y))≤m‖x-y‖μ,其中H表示Hausdorff度量.
(ii)称F在C上是γ-严格单调的,如果存在常数L>0,γ>0使得
〈u-v,x-y〉≥L‖x-y‖1+γ,∀u∈F(x),v∈F(y).
(iii)称F在C上是γ-一致P-映射,如果存在常数L>0,γ>0使得

对任意x∈Rn,令
PC(x)=argmin{‖x-y‖y∈C},
PC(x)称为x在C上的投影,PC(·)称为Rn到C上的投影算子.
性质1[9]设C为Rn上的非空闭凸集,对投影算子PC(·),有下面结论成立:
(i)对任意x∈Rn,y∈C有〈PC(x)-x,y-PC(x)〉≥0.
(ii)对任意x,y∈Rn有‖PC(x)-PC(y)‖≤‖x-y‖.
对任意x∈C,ξ∈F(x),变分不等式(1)的投影残量为e(x)=x-PC(x-βξ),为便于后面证明, 令β>0,且r(x)=‖e(x)‖.
引理1[10]x∈Ω的充分必要条件是r(x)=0.
2 广义集值变分不等式的误差界的估计
本节主要借助投影残量研究广义集值变分不等式(1)的误差界.根据引理1,有下面结论
引理2 假设F(x)在C上是γ-严格单调,若广义集值变分不等式(1)有解,则解惟一.
证明设x*∈Ω,所以存在ξ1∈F(x*),对任意y∈C满足
〈ξ1,y-x*〉≥0
(3)
对任意x∈C,ξ∈F(x),β>0,在式(3)中令y=PC(x-βξ),我们有
〈βξ1,PC(x-βξ)-x*〉≥0
(4)
由性质1的(i)和x*∈C知
〈PC(x-βξ)-(x-βξ),x*-PC(x-βξ)〉≥0
(5)
式(4)与式(5)相加得
〈PC(x-βξ)-(x-βξ)-βξ1,x*-PC(x-βξ)〉=
〈βξ-βξ1-e(x),e(x)+x*-x〉=〈β(ξ-ξ1)-e(x),e(x)〉+〈β(ξ-ξ1)-e(x),x*-x〉=
〈β(ξ-ξ1),e(x)〉-〈e(x),e(x)〉-〈β(ξ-ξ1),x-x*〉+〈e(x),x-x*〉≥0,
故可得到
〈β(ξ-ξ1)+x-x*,e(x)〉≥〈β(ξ-ξ1),x-x*〉
(6)
由于F(x)在C上是γ-严格单调的,所以存在常数L>0,γ>0使得
Lβ‖x-x*‖1+γ≤〈β(ξ-ξ1),x-x*〉,
结合式(6)得到
Lβ‖x-x*‖1+γ≤r(x)(β‖ξ-ξ1‖+‖x-x*‖)
(7)
若x∈Ω,由引理1知,r(x)=0,由式(7),我们可以得到x=x*.故结论成立.
根据引理2,建立问题(1)的误差界.
定理1 假设F(x):C→2Rn为Hølder连续和γ-严格单调,且满足

则对任意x∈C,ξ∈F(x)有
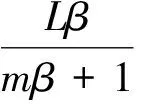

证明对任意x*∈Ω,存在ξ1∈F(x*),对任意x∈C,ξ∈F(x),由(7)和F(x)在C上Hølder连续知,
Lβ‖x-x*‖1+γ≤r(x)(β‖ξ-ξ1‖+‖x-x*‖)≤r(x)(βm‖x-x*‖μ+‖x-x*‖)
(8)
若‖x-x*‖≤1,则由(8)知
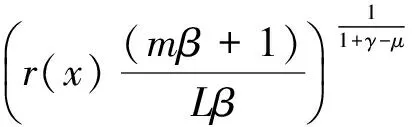
(9)
若‖x-x*‖≥1,则由(8)知

(10)
另外由引理1和性质1(ii)知
r(x)=‖e(x)-e(x*)‖=‖x-PC(x-βξ)-(x*-PC(x*-βξ1))‖≤
‖x-x*‖+‖PC(x-βξ)-PC(x*-βξ1)‖≤‖x-x*‖+‖x-βξ-(x*-βξ1)‖≤
2‖x-x*‖+β‖ξ-ξ1‖≤2‖x-x*‖+mβ‖x-x*‖μ
(11)
当‖x-x*‖≤1时,由式(11)知

(12)
当‖x-x*‖≥1时,由式(11)知

(13)
结合(9)和(12),我们得到

(14)
结合(10)和(13),我们得到
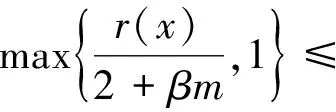
(15)
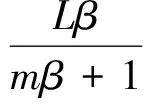

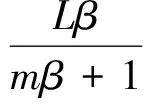
3 广义集值非线性互补问题的误差界
本节主要讨论了广义集值非线性互补问题(2)的误差界,首先给出以下引理.
引理3 如果a,b∈R,a*,b*∈R+,a*b*=0,则
[a-a*-min{a,b}][b-b*-min{a,b}]≤0.
证明当a≤b时,可得[a-a*-min{a,b}][b-b*-min{a,b}] =[a-a*-a]b-b*-a] =-a*[b-a] ≤0,同理当a≥b时,亦可得到[a-a*-min{a,b}][b-b*-min{a,b}]≤0,故结论成立.
根据引理3,对于广义集值非线性互补问题(2),在相对弱条件下,我们建立了问题(2)的误差界.

L≤(2+mβ)(1+mβ)/β,
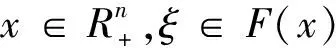
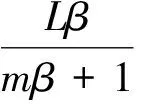
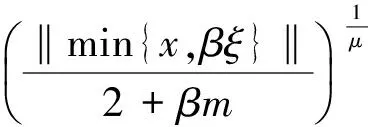
(ii)当‖min{x,βξ}‖≥2+mβ时,
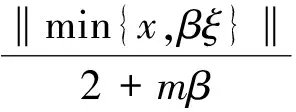


可得
0≥[βξi-β(ξ1)i-min{xi,βξi}][xi-(x*)i-min{xi,βξi}]=
β[ξi-(ξ1)i][xi-(x*)i]-β[ξi-(ξ1)i]min{xi,βξi}
-min{xi,βξi}[xi-(x*)i]+min{xi,βξi}min{xi,βξi}≥
β[ξi-(ξ1)i][xi-(x*)i]-min{xi,βξi}{β[ξi-(ξ1)i]+[xi-(x*)i]}.
所以
β[ξi-(ξ1)i][xi-(x*)i]≤min{xi,βξi}{β[ξi-(ξ1)i]+[xi-(x*)i]}.
由于集值映射F是Hølder连续的和γ-一致P-映射,结合上式得
Lβ‖x-x*‖1+γ≤‖min{x,βξ}‖[mβ‖x-x*‖μ+‖x-x*‖]
(12)
再结合式(11),类似于定理1证明,易推得结论(i)~(iii)成立.
[1] Noor M A. General variational inequalities[J]. Appl Math Lett, 1986, 1: 119-121.
[2] Xiu N H, Zhong J Z. Golbal projection-type error bound for general variational inequalities[J]. J Optim Theory Appl, 2002, 112(1): 213-228.
[3] Pang J S. A posterriorl error bound for the linearly-constrained variational inequality problem[J]. Math of Operations Research, 1987, 12: 474-484.
[4] Solodov M V. Convergence rate analysis of iterative alagorithm for solving variational inequality problem[J]. Math Programming, 2003, 96:513-528.
[5] Solodov M V. Merit functions and error bounds for generalized variational inequalities[J]. J Math Appl, 2003, 287: 405-414.
[6] Noor M A. Merit functions for generalized variational inequalities[J]. J Math Appl, 2006, 316: 736-752.
[7] Li F L, He Y R. An algorithm for generalized variational inequality with pesudomonotone mapping[J]. J Compute Appl Math, 2009, 228: 212-218.
[8] 方长杰, 何诣然. 广义变分不等式的优质泛函[J]. 四川师范大学学报, 2001, 34(4): 68-72.
[9] Facchinei F, Pang J S. Finite-dimensional varitional inequalities and complementarity problem[M]. New York: Springer, 2003.
[10] Kinderlehrer D, Stamppacchia G. An introduction to varitional inequalities and their applications[M]. New York: NY Academic Press, 1980.
ErrorBoundforGeneralizedVariationalInequalityandComplmentarityProblemwithSet-valuedMapping
LI Li1,2, ZHOU Hou-chun1
(1.School of Science, Linyi University, Linyi Shandong 276005, China)(2.School of Mathematical Science, Shandong Normal University, Jinan Shandong 250014, China)
Based on the projection residue of generalized variational inequality, we establish error bound estimation for generalized variational inequality with multi-valued mapping (generalized nonlinear complementarity problem with multi-valued mapping) over a closed convex polyhedral with the underlying mapping beingγ-strict monotone (γ-uniformP-mapping) and Hølder continuous, respectively, and our result which can be taken as an extension of the result of generalized for variational inequality(generalized nonlinear complementarity problem).
multi-valued mapping; generalized variational inequality; generalized nonlinear complementarity; error bound
2012-11-03
国家自然科学基金资助项目(11271226); 山东省自然科学基金资助项目(ZR2010AL005, ZR2011FL017); 2012年物流教改教研课题计划项目(JZW2012065)
李丽(1987-), 女, 宁夏吴忠人, 硕士研究生, 研究方向为图论与组合优化.
O242
A
1671-6876(2013)01-0005-04
[责任编辑李春红]

