Banach空间上的双参数正则化

李 想

(成都理工大学 应用数学系, 四川 成都 610059)

Banach空间上的双参数正则化

李 想

(成都理工大学 应用数学系, 四川 成都 610059)

在Banach空间中,研究了非线性不适定问题的正则化.引入并且推广了一种双参数的Tiknonv正则化方法,讨论了这种方法解得存在性、稳定性和收敛性.

非线性; 不适定问题; 双参数正则化; 收敛性

0 引言

Tikhonov正则化方法是求解非线性不适定算子方程

F(u)=v0

(1)

的常用工具.本文假设U、V是自反的严格凸的Banach空间,算子F:D(F)⊂U→V.Grasmair M.[1]考虑了罚项为lq的稀疏正则化;杨宏奇等[2]研究了Banach空间中的多值算子;李招文等[2]对于求解 Hilbert 空间非线性不适定问题引入了双参数正则化方法,即用极小化问题

其中α>0,β>0的解去逼近问题(1) 的解.本文将用双参数正则化问题解决Banach空间非线性不适定问题,将极小化泛函推广为

(2)

其中α>0,β>0,并研究其适定性.

为了下文叙述的方便,首先给出相关定义和假设条件.

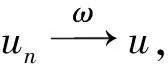
定义2u0是方程(1) 的一个u*-极小范数解(u*-MSS),即对于v0∈V,u*∈D(L),满足F(u0)=v0,并且‖Lu0-Lu*‖=min{‖Lu-Lu*‖:F(u)=v0}.

定义3 在D(L) 中引入一个新的范数‖u‖L=‖u‖U+‖Lu‖W,记为空间H=(D(L),‖·‖L).易知,H仍是一个Banach空间.

本文假定下列条件满足

(i)D(F)⊂D(L);

(ii) (F,L):D(F)⊂U→V×W弱序列闭,即,任意序列{un}⊂D(F),若

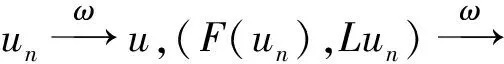
(iii) {un}⊂D(F),若{F(un),Lun}有界,则{un}有界;

1 最小化问题解的存在性和稳定性

这部分我们将证明最小化问题解的存在性和稳定性.

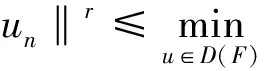
又根据范数的弱下半连续性可知

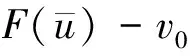
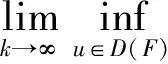
而

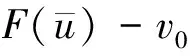
定理2 若假设条件(ii)、(iii)满足,对于给定的α,β,{vn}⊂V,vn→v0,un为极小化问题

(3)

的一个解,则序列{un}一定存在一个在H中收敛的子序列{unk},且其极限是极小化问题(2) 的一个解.

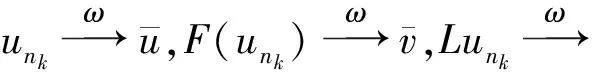
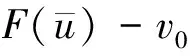
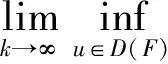
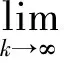
‖F(u)-v0‖p+α‖Lu-Lu*‖q+β‖u‖r,

由范数弱下半连续性有

(4)

所以,存在正整数N,使得k≥N时有

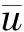
又由vnk→v0,可知‖F(u)-vnk‖p→‖F(u)-v0‖p,故k≥N时有

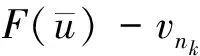
即

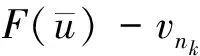
由(4) 知,当k≥N时有

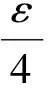
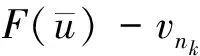
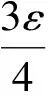
‖F(unk)-vnk‖p+α‖Lunk-Lu*‖q+β‖unk‖r+ε-βρ<

‖F(unk)-vnk‖p+α‖Lunk-Lu*‖q+β‖unk‖r,

2 正则解的收敛性

这部分我们将证明最小化问题解的存在性和稳定性.

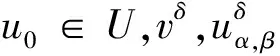
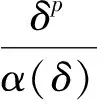
则对δk→0αk=α(δk),βk=β(δk),我们有结论

所以F(uk)有界,从而{(uk,F(uk),Luk)}在空间U×V×W有界.

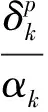
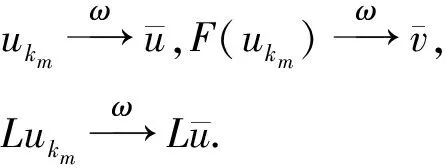
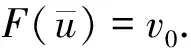
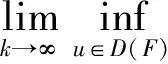
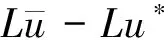
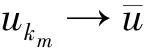
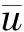
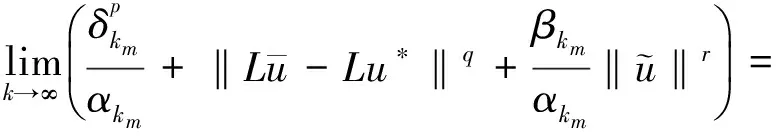
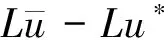
[1] Grasmair M, Haltmeier M, Scherzer O. Sparse regularization with lqpenalty term[J]. Inverse Problems, 2008, 24(5): 55-20.

[2] 杨宏奇, 侯宗义. 非线性不适定算子方程的双参数正则化方法[J]. 数学物理学报, 2004, 24A(1): 129-134.

[3] 李招文, 李景, 刘振海. 非线性不适定问题的双参数正则化[J]. 中国科学, 2007, 37(9): 1117-1124.

[4] Groetsch C W.The Theory of Tikhonov Regularization for Fredholm Equations of the First Kind[M]. Boston: Pitman,1984.

Two-parameterRegularizationMethodinBanachSpace

LI Xiang

(Department of Applied Mathematics, Chengdu University of Technology, Chengdu Sichuan 610059, China)

This paper deals with the regularization of a nonlinear ill-posed problem in Banach space. We present and popularize a kind of two-parameter regularization method, and discuss the existence, stability, convergence of the solution of this method.

nonlinear; ill-posed problem; two-parameter tikhonov regularization; convergence rate

2012-10-12

李想(1989-), 女, 山东威海人, 硕士研究生, 研究方向为应用泛函分析.

O177.91; O241.7

A

1671-6876(2013)01-0021-04

[责任编辑李春红]