序列{Un}模素数幂的同余式

朱长艳

(1.江苏师范大学 数学科学学院, 江苏 徐州 221116; 2.淮阴师范学院 数学科学学院, 江苏 淮安 223300)

序列{Un}模素数幂的同余式

朱长艳1,2

(1.江苏师范大学 数学科学学院, 江苏 徐州 221116; 2.淮阴师范学院 数学科学学院, 江苏 淮安 223300)

设{Un}是如下定义的序列:

这里[x]为取整函数,本文利用孙智宏建立的同余式,获得U2n(mod 35),U2n(mod 2α+16)(n≥8且2α|n)以及U32k+b-Ub(mod 256)的同余式．

序列; 求和公式; 同余式

0 引言

设[x]表示不超过x的最大整数,Euler数{En}由下式给出:

在文[4]中孙智宏引入类似于Euler数的如下序列{Un}:

在文[5]中孙智宏证明了恒等式

和

还证明了同余式

U2n≡1-3n(mod27)

(1)

和

U2n≡-16n-42(mod27)(n≥3)

(2)

在文[6]中孙智宏还证明了当n≥5且2α|n时有

3U2n+27n(2n-1)U2n-2≡2(72n+62n-42n-32n+1)+216+2α(n-1)

-23·213n(n-1)+7·215n(n-1)3(mod2α+19)

(3)

和当n≥7且2α|n时有

3U2n≡-3072n4+4608n3+2240n2+1680n+2(mod2α+14)

(4)

本文用式(1)证明了

U2n≡-72n3+108n2-39n+1(mod35).

用式(2)、式(3)和式(4)证明了当n≥8且2α|n时有

3U2n≡5120n4+12800n3-30528n2-31088n+2(mod2α+16).

最后还证明了孙智宏的猜想U32k+b-Ub(mod256),见定理3.

1 相关引理

为了证明文中的主要结论,首先引入一个引理

引理1 设n≥5为自然数,则有

U2n≡-448n2-464n+342(mod210).

证明由

及式(2)知

+43·22n+42)(mod210).

由二项式定理知

又

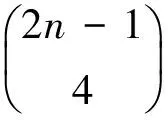
故

当n≥5时

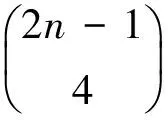
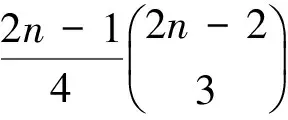
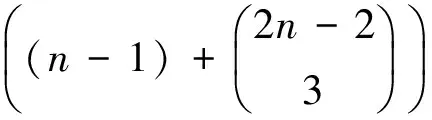
显然有

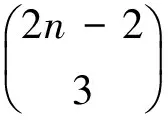
3(n-1)((6-2n)+1)=3(n-1)(7-2n)(mod8),

和

27n(2n-1)·3(n-1)(7-2n)=-3·27n(n-1)((2n-1)2-6(2n-1))≡

-3·27n(n-1)(1-6(2n-1))=-3·27n(n-1)+9·27n((2n-1)2-(2n-1))≡

-3·27n(n-1)+9·27n(1-(2n-1))=-21·27n(n-1)(mod210).

从而

3U2n≡-21·27n(n-1)+21·26n2+16n+2=

21·26n(n-2(n-1))+16n+2=21·26n(2-n)+16n+2≡

5·26n(2-n)+16n+2=-320n2+656n+2≡-320n2-368n+2(mod210).

于是

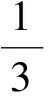
5×320n2+21×368n-682=1600n2+7728n-682≡-448n2-464n+342(mod210).

2 主要结论

定理1 设n为自然数,则有

U2n≡-72n3+108n2-39n+1(mod35).

证明由于

故由式(1)知

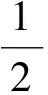
由二项式定理知

和

则有

从而

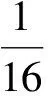
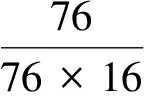
76(81n4-90n3+54n2-141n)+2+54n3-81n2+27n≡

81n4-36n3-27n2-24n+2+54n3-81n2+27n=

81n4+18n3-108n2+3n+2≡-162n4+18n3-108n2-240n+2(mod35).

于是

U2n≡-81n4+9n3-54n2-120n+1=

-81[(n-1)n(n+1)(n+2)-2n3+n2+2n]+9n3-54n2-120n+1≡

-81(-2n3+n2+2n)+9n3-54n2-120n+1=

171n3-135n2-282n+1≡-72n3+108n2-39n+1(mod35).

定理2 当n≥8为自然数且2α|n时,有

3U2n≡5120n4+12800n3-30528n2-31088n+2(mod2α+16).

证明当n≥6时,由引理1知

U2n-2≡-448(n-1)2-464(n-1)+342=-448n2+432n+358(mod210),

由式(3)得

3U2n+27n(2n-1)(-448n2+432n+358)≡

2(72n+62n-42n-32n+1)-23·213n(n-1)+7·215n(n-1)3(mod2α+16).

当2n≥α+15时,有62n≡42n≡0(mod2α+15),且有

27n(2n-1)(-448n2+432n+358)=28(-448n4+656n3+142n2-179n).

由于

24·213n(n-1)=3·216n(n-1)≡0(mod2α+16),

8·215n(n-1)3=218n(n-1)3≡0(mod2α+16).

故

3U2n≡28(448n4-656n3-142n2+179n)+2(72n-32n+1)+

213n(n-1)-215n(n-1)3(mod 2α+16).

由二项式定理知

故

40n+1120n(n-1)+7424n(n-1)(n-2)-5632n(n-1)(n-2)(n-3)=

-5632n4+41216n3-83104n2+47560n≡

-5632n4+8448n3+15200n2+14792n(mod 2α+15).

于是

3U2n≡28(448n4-656n3-142n2+179n)+2(-5632n4+8448n3+15200n2+

14792n+1)+213n(n-1)-215n(n-1)3=

70656n4-52736n3-96064n2+99984n+2≡

5120n4+128003-30528n2-31088n+2(mod 2α+16).

定理3 设k为正整数,b为非负偶数,则有

证明由引理1知

U2n≡64n2+48n+86(mod256)(n≥4).

故

U32k+b-Ub≡16(32k+b)2+24(32k+b)+86-Ub≡16b2+24b+86-Ub(mod256).

从而

当b=0时,U32k-U0≡86-1=85(mod256),

当b=2时,U32k+2-U2≡16·22+24·2+86+2=200(mod256),

当b=4时,U32k+4-U4≡16·42+24·4+86-22≡96+86-22=160(mod256),

当b=6时,U32k+6-U6≡16·62+24·6+86+602=1048≡128(mod256),

当b≥8时,U32k+b-Ub≡16·b2+24·b+86-(16·b2+24·b+86)=0(mod256).

致谢: 作者感谢本文指导老师淮阴师范学院孙智宏教授的悉心指导!

[1] Chen K W. Congruences for Euler numbers[J]. Fibonacci Quart, 2004,42:128-140.

[2] Magnus W, Oberhettinger F,Soni R P. Formulas and Theorems for the Special Functions of Mathematical Physics[M]. 3rd edition. New York: Springer,1979,139-159.

[3] Sun Z H. Euler numbers modulo 2n[J].Bull Austral Math Soc, 2010, 82: 221-231.

[4] Sun Z H, Congruences for sequences similar to Euler numbers[J]. J Number Theory, 2012, 132: 675-700.

[5] Sun Z H. Identities and congruences for a new sequence[J]. Int J Number Theory, 2012, 8: 207-225.

[6] Sun Z H. Some properties of a sequence analogous to Euler numbers[J]. Bull Austral Math Soc, 2013,87(3). http://journals.cambridge.org/action/displayAbstract fromPage=online&aid=8607855.

CongruencesfortheSequences{Un}ModuloPrimePowers

ZHU Chang-yan1,2

(1.School of Mathematical Science, Jiangsu Normal University, Xuzhou Jiangsu, 221116, China)(2.School of Mathematical Science, Huaiyin Normal University, Huaian Jiangsu, 223300, China)

The sequence {Un} is defined by

where [x] is the greatest integer not exceedingx. In the paper,by using the congruences established by Zhi-Hong Sun, we obtain the congruences forU2n(mod 35),U2n(mod 2α+16)(n≥8 and 2α|n) andU32k+b-Ub(mod 256).

sequence; summation formula; congruence

2012-09-26

朱长艳(1986-), 女, 江苏连云港人, 硕士研究生, 研究方向为运筹学与控制论.

O231

A

1671-6876(2013)01-0009-06

[责任编辑李春红]