Fibonacci数的标准分解式中素因数17的指数

林伟芬, 尤利华

(华南师范大学 数学科学学院, 广东 广州 510631)

Fibonacci数的标准分解式中素因数17的指数

林伟芬, 尤利华

(华南师范大学 数学科学学院, 广东 广州 510631)

研究了Fibonacci数Fn的标准分解式中素因数17的指数与下标n的关系,证明了Fibonacci数Fn的标准分解式中素因数17的指数由下标n的分解式中因数9的指数与17的指数来确定.

Fibonacci数; 标准分解式; 素因数; 指数; 同余

0 引言

Fibonacci数起源于数学家P.Leonardo提出的“兔子问题”[1].因为Fibonacci数具有一些特殊性质以及重要应用,所以一直引起许多学者的关注,同时也吸引着许多理论和应用研究专家的研究兴趣.

定义1[2-3]Fibonacci数列是指由初始条件F0=0,F1=1和递推关系Fn=Fn-1+Fn-2(n≥2)所确定的数列{Fn}n≥0,这里称Fn为Fibonacci数.

对于Fibonacci数的标准分解式中素因数的指数的有关研究,文[4-9]得到了素因数为2,3,5,7,11,13的相关结果.文[10-11]给出了Fibonacci数的一些整除性质.尤利华[12]对一般的奇素因数p与d(p)=min{w:p/Fw}的整除关系进行了研究,并提出了一个关于在p的Fd(p)标准分解式中的指数的猜想.本文在上述工作的前提下,证明了Fibonacci数Fn的标准分解式中素因数17的指数可由下标一的分解式中因数9的指数与17的指数来确定.

引理1 设m,n为正整数,若m|n,则Fm|Fn,这里记号“a|b”表示a整除b.

引理2 设m,k为正整数,则Fm+k=FmFk-1+Fm+1Fk.

引理3 设m为非负整数,则 (Fm,Fm+1)=1.

引理4 设n为正整数,则17|Fn⟺9|n.

证明由同余式

Fn+36=FnF35+Fn+1F36=9227465Fn+19430352Fn+1≡9227465Fn≡Fn(mod17),

且由Fibonacci数列的定义及同余的可加性,计算Fi(0≤i≤35)关于模17的最小非负剩余,可得:

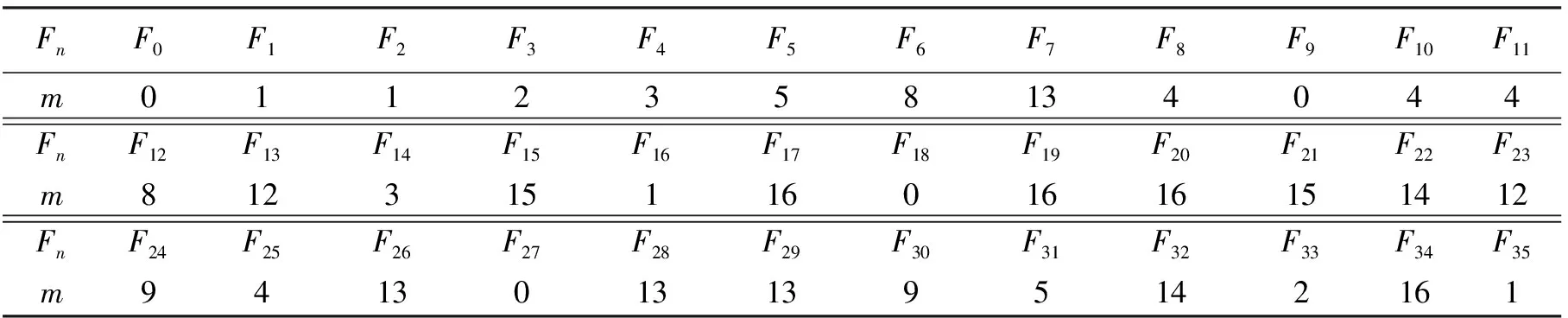
表1 关于模17的最小非负剩余

故在Fibonacci数列中,Fn关于模17的最小非负剩余是以36为周期变化的,且Fn≡0(mod17)当且仅当n≡0(mod9),即17|Fn⟺9|n.

引理5 设m是正整数,则F9m+1≡F9m-1(mod17)

证明由引理4及Fibonacci数的定义知,F9m=F9m+1-F9m-1≡0(mod17),故引理5成立.

1 主要结果及其证明

引理6 设m,p为正整数,则

证明(i)对p应用数学归纳法:

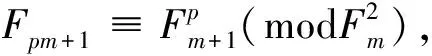
由引理1知Fm|Fpm,又由引理2有

(ii)同样对p应用数学归纳法:

由引理2知

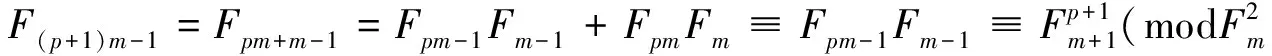
定理1 设k,p为正整数,则F9kp与F9k+1p的标准分解式中素因数17的指数相同.

证明由引理4易得17|F9kp,故在F9kp的标准分解式中,素因数17的指数必大于0,可设为s(s≥1),又设n=9kp,对取定的正整数p,对Fn的下标n的分解式中因数9的指数k用数学归纳法证明.

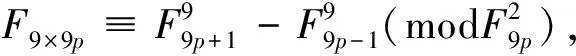
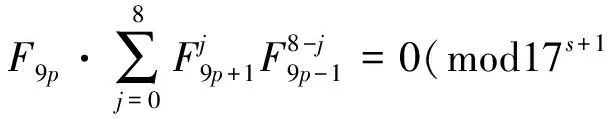
(ii) 假设当k≥1时结论都成立,即F9kp与F9k+1p的标准分解式中素因数17有相同的指数s(s≥1).下证对k+1也能成立,等价于证明F9k+1p与F9k+2p的标准分解式中素因数17的指数也为s.

因为9k+1p|9k+2p,由引理1有F9k+1p|F9k+2p从而有F9k+2p≡0(mod17s).

综上(i)(ii)所述知,定理1得证.

定理2 设p为不含9和17的正整数,则F9p的标准分解式中素因数17的指数为1.

证明因为9|9p,由引理1有F9|F9p,从而有F9p≡0(mod17),下证F9p不能被172整除.

不妨设p=17m+r,1≤r≤16,则F9p=F9×(17m+r)=F9×17m+9r=F9×17mF9r-1+F9×17m+1F9r.

运用同样的证明方法可得下面定理3.

定理3 设p为不含9和17的正整数,则F9×17p的标准分解式中素因数17的指数为2.

定理4 设n=9×17sp,其中p为不含9和17的正整数,而s是任意非负整数,则F9×17sp的标准分解式中素因数17的指数为s+1.

证明对任意取定的正整数p,对n的分解式中17的指数应用数学归纳法证明.

(i) 当s=0时,n=9p,由定理2知,F9p的标准分解式中素因数17的指数为s+1=1,此时结论成立.

(ii) 当s=1时,n=9×17p,由定理3知,F9×17p的标准分解式中素因数17的指数为s+1=2,此时结论也成立.

令m=9×17sp,则由引理2有

F9×17s+1p=F17m=F(9+8)m=F9mF8m-1+F9m+1F8m

(1)

(2)

(3)

(4)

由引理5知F9×17sp+1≡F9×17sp-1(mod17)即Fm+1≡Fm-1(mod17),又17|Fm,且由引理1,引理6可得

(5)

由式(1)-(5)可得

由F9×17sp的标准分解式中素因数17的指数为s+1可知

所以

(6)

当s≥1时,有2(s+1)≥s+3,则由引理5及9|m知,Fm+1≡Fm-1(mod17)且其最小非负剩余不是0,代入式(6)得

(7)

下证17s+3不能整除F9×17s+1p.

由式(6)有

(8)

由引理5及表1不妨设Fm+1=17q1+r,Fm-1=17q2+r,这里r=1,4,13,16,q1,q2为非负整数.从而

(0×17q1r15+16×17q2r15+r16)+(1×17q1r15+15×17q2r15+r16)

+…+(8×17q1r15+8×17q2r15+r16)+8×(9×17q1r15+7×17q2r15+r16)≡

(1+2+…+8)×17q1r15+(16+15+…+8)×17q2r15+

9r16+72×17q1r15+56×17q2r15+8r16≡

17×(r+108q1+164q2)r15(mod172)

(9)

综上所述及数学归纳法可知,定理4成立.

最后给出一个总结性定理如下.

定理5 设n为正整数,且n=9k×17s×p,这里k,s为非负整数,p为不含因数9和17的正整数,则

1) 当k=0时,Fn的标准分解式中素因数17的指数为0;

2) 当k≥1时,Fn的标准分解式中素因数17的指数为s+1.

证明1)当k=0时,n不被9整除,由引理4知,17不能整除Fn,即Fn的标准分解式中素因数17的指数为0.

2)当k≥1时,由定理1知,在F9kp与F9k+1p的标准分解式中素因数17的指数相同,所以只需考虑k=1的情形.又由定理4可知,F9×17sp的标准分解式中素因数17的指数为s+1.

从而定理5成立.

[1] 曹汝成. 组合数学[M].广州:华南理工大学出版社,2006:91-98.

[2] 闵嗣鹤,严士建. 初等数论[M].3版.北京:高等教育出版社,2003.

[3] [苏]瓦罗别耶夫. 斐波那契数列[M].哈尔滨:哈尔滨工业大学出版社,2009.

[4] 袁明豪. 正Fibonacci数的标准分解式中因子2的指数[J].数学通讯,2003(15):26-27.

[5] 袁明豪. 正Fibonacci数的标准分解式中因子3的指数[J].荆州师范学院学报:自然科学版,2003,26(2):12-13.

[6] 袁明豪. 正Fibonacci数的标准分解式中因子5的指数[J].数学的实践与认识,2007,37(7):166-170.

[7] 王念良,张洁. Fibonacci数的标准分解式中因子7的指数[J].商洛学院学报,2007,21(4):4-7.

[8] 林丽荣,尤利华. Fibonacci数的标准分解式中素因数11的指数[J].甘肃联合大学学报,2008,22(6):4-10.

[9] 黄荣辉,尤利华. Fibonacci数的标准分解式中素因数13的指数[J].江西师范大学学报,2012,36(3):234-237.

[10] 袁明豪. Fibonacci数的一组整除特征[J].数学通讯,2004(15):29-31.

[11] 吴佃华,贾小英. Fibonacci数的整除性[J].广西师范学院学报,2007,24(3):28-29,60.

[12] 尤利华,黄荣辉.Fibonacci数的标准分解式中诸奇素因数的指数[J].广西师范大学学报,201l,29(3),18-22.

TheExponentofFactor17intheStandardFactorizationofFibonacciNumber

LIN Wei-fen, YOU Li-hua

(School of Mathematical Science, South China Normal University, Guangzho Guangdong 510631, China)

In this paper, the relationship between the exponent of factor 17 in the standard factorization of Fibonacci NumberFnand its subscript n are studied, and it is shown that the exponent of factor 17 in the standard factorization of Fibonacci NumberFncan be found out by the exponent of 9 and 17 in the factorization of the subscriptn

fibonacci number; standard factorization; factor; exponent; congruence

2013-06-26

国家自然科学基金青年基金项目(10901061)

林伟芬(1990-), 女, 广东汕头人, 硕士研究生, 研究方向为数学教育.

O156

A

1671-6876(2013)03-0213-05

[责任编辑李春红]