关于单个总体均值的半参数假设检验方法

方 芳

(南京财经大学 应用数学学学院, 江苏 南京 210023)

关于单个总体均值的半参数假设检验方法

方 芳

(南京财经大学 应用数学学学院, 江苏 南京 210023)

提出一种半参数的假设检验方法,将它应用于对单个总体均值的假设检验.最后给出了实例分析．

半参数; 假设检验; 总体均值

0 引言

近些年有不少学者致力于在半参数密度函数比模型下建立半参数统计方法,比如Qin[1]研究了在密度函数比模型下如何对混合比例进行半参数的统计推断.Zhang[2]研究了半参数的分位数估计方法,Qin和Zhang[3]建立了在半参数函数密度比模型下进行ROC曲线估计的半参数方法Folkianos[4],Cheng和Chu[5],以及Qin 和 Zhang[6]建立了半参数的密度函数估计方法Wan 和 Zhang[7-8]建立了在半参数函数密度比模型下进行ROC曲线比较和估计的半参数方法.Wan[9]提出了用半参数方法对两总体均值差进行假设检验.

对于总体均值的检验,在知道总体分布服从正态分布的情况下可以用t检验.在样本量很大时用u检验,那么在总体分布未知或者样本量不大的情况下有没有一种有效的方法呢?Wan已经在两总体半参数密度比模型下对两总体均值差进行了假设检验.本文致力于在两总体半参数密度比模型下,对两总体中的任一总体均值进行假设检验.

对于两样本{x1,x2,x3,…xn0}{z1,z2,z3,…zn1},QIN和Zhang[10]建立了半参数密度比模型:

x1,x2,x3,…,xn0相互独立并且密度函数为g(x),

z1,z2,z3,…,zn1相互独立并且密度函数为f(x)=exp(α+xβ)g(x).

此模型为有偏样本模型,权函数为exp(α+xβ),α,β为一维标量.在这里我们可考虑多维形式,则改进后的模型为:

x1,x2,x3,…,xn0相互独立并且密度函数为g(x),

z1,z2,z3,…,zn1相互独立并且密度函数为f(x)=exp(α+βTr(x))g(x).

这里α是一个标量参数,β为p×1的向量函数,r(x)是一个p×1的关于x的光滑的向量函数.由于模型中不要求g(x),f(x)是某个具体的分布,因而不是传统的参数模型,同时又含有参数α,β,故又不是传统的非参数模型在这里我们称之为介于参数与非参数之间的半参数模型.

1 主要理论知识

我们可以将两总体的样本{x1,x2,x3,…,xn0}和{z1,z2,z3,…,zn1}合并为样本{t1,t2,…,tn},则根据上面改进后的模型里观察到的数据,可以写出相应的半参数经验似然函数:

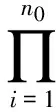
我们根据文献[9]知在改进后的模型下G(t)的最大半参数似然估计量为

于是我们可以通过代入G(t)的估计量来获得分布函数为G(t)的总体均值的最大似然估计量

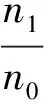
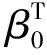
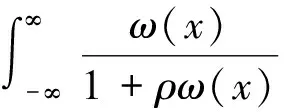
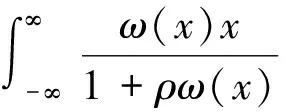
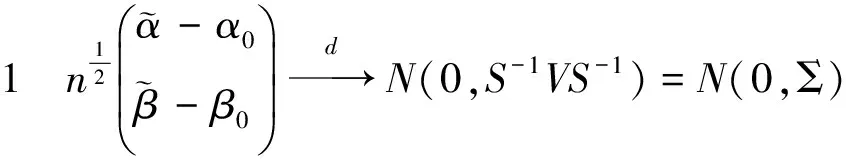
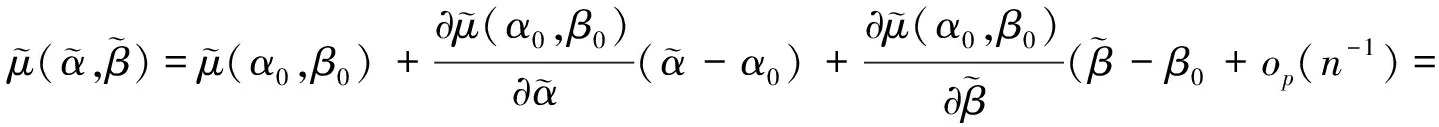
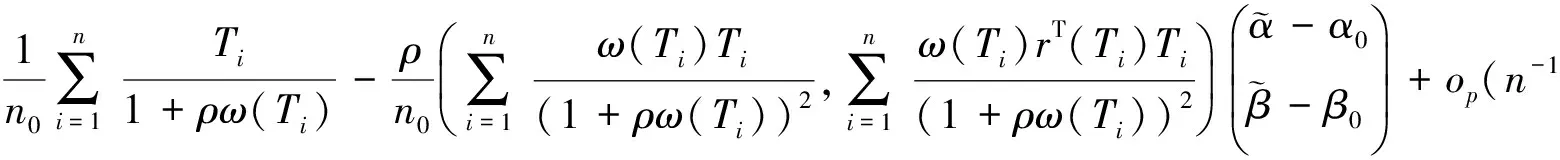
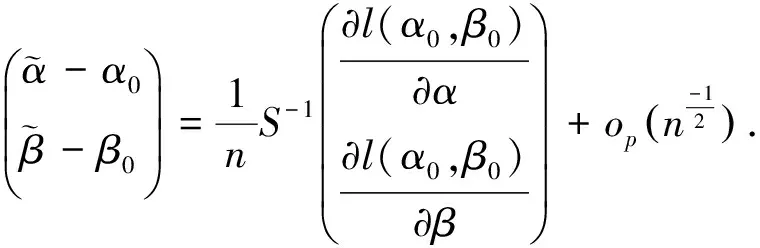
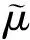
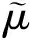
则经过计算得

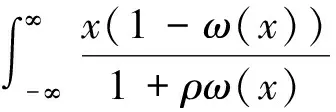
化简可得

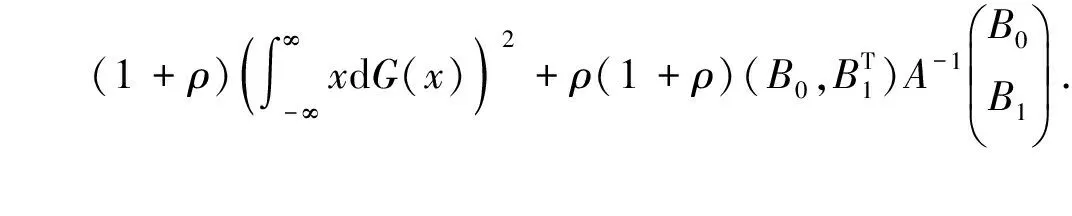
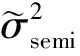
其中

现在考虑在改进后的模型下进行假设检验H0:μ=θ0,H1:μ≠θ0.

根据定理1可以构造一个半参数的Wald统计量

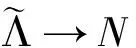
2 实例分析

例1 某切割机在正常工作时, 切割每段金属棒的平均长度为10.5cm, 今从一批产品中随机的抽取15段如:10.4,10.6;10.1,10.4,10.5,10.3,10.3,10.2,10.9,10.6,10.8,10.5,10.7,10.2,10.7进行测量, 则该机工作是否正常．

建立假设检验H0:μ=10.5H1:μ≠10.5.

(i) 若切割的长度服从正态分布,且标准差已知,假定标准差为0.15,则可以根据单个总体均值u检验,得到

因此我们不可以拒绝原假设．该机工作正常.

(ii) 若切割的长度服从正态分布,且标准差未知,则根据单个总体均值t检验,得到

[1] Qin J. Empirical likelihood ratio based confidence intervals for mixture proportions[J].Ann Statist,1999,27:1368-1384.

[2] Zhang B.Quantile estimation under a two-sample semi-parametric model[J].Bernooulli,2000,6:491-511.

[3] Qin J. Zhang B.Using logistic regression procedures for estimating receiver operating characteristic curves[J].Biometrika,2003,90:585-596.

[4] Fokianos K. Merging information for semiparametric density estimation[J].J Roy Statist Soc Ser B,2004,66:941-958.

[5] Cheng K,Chu C. Semiparametric density estimation under a two-sample density ratio model[J].Bernoulli,2004,10:583-604.

[6] Qin J,Zhang B. Density estimation under a two-sample semiparametric model[J].J NonparametrStatist,2005,17:665-683.

[7] Wan S,Zhang B. Smooth semiparametric receiver operating characteristic curves for continuous diagnosic tests[J].Statist Med,2007,26:2565-2586.

[8] Wan S,Zhang B. Comparing correlated ROC curves for continuous diagnostic tests under density ratio models[J].Comput Statist Data Anal,2008,53-245.

[9] 万树文,方芳. 关于两总体均值差的一种半参数假设检验方法[J].中国科学:数学.2012,42(7):671-679.

[10] Qin J,Zhang B. A goodness of fit test for logistic regression models based on case-control data[J].Biometrika,1997,84:609-618.

ASemiparametricHypothesisTestingMethodonthePopulationMean

FANG Fang

(School of Applied Mathematics, Nanjing University of Finances and Economics, Nanjing Jiangsu 210023, China)

In this paper, we propose a semi-parametric hypothesis testing method,it would be applied to a single population mean hypothesis testing, and gives examples of analysis

semi-parametric; hypothesis testing; the population mean

2013-05-20

方芳(1988-), 女, 安徽六安人, 硕士研究生, 研究方向为数理统计．

O211

A

1671-6876(2013)03-0204-04

[责任编辑李春红]