基于数据的MATLAB系统辨识工具箱模型识别
陈岚峰,张亚琴,程立英,张志美
(1.沈阳师范大学 物理科学与技术学院,沈阳 110034;2.沈阳师范大学 实验教学中心,沈阳 110034)
0 引 言
利用控制理论去解决实际问题时,首先需要建立被控对象的数学模型[1]。现代复杂工程系统越来越趋近于多元化、模块化[2],实际工程中存在着大量控制对象要建立用于描述其行为特性的数学模型,系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型,是现代控制理论中的一个分支。随着各门科学的定量化,系统辨识的应用越来越广泛,不仅是航空、航天、电力、化工等工程应用领域,还延伸到生物信息科学、医学工程、社会经济等各学科[3]。
1 系统辨识基本理论
系统辨识是在对输入和输出观测的基础上,在指定的一类系统中,确定一个与被识别的系统等价的系统[4]。系统辨识理论是通过考察输入输出数据来建立动态系统模型的科学技术,是联系控制理论和数学模型的抽象世界与实际应用的现实世界的接口[5]。对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
2 系统辨识方法
辨识的实质就是从一组模型类中选择一个模型,按照某种准则,使之能最好地拟合所关心的实际过程的静态或动态特性。常用的系统辨识方法有最小二乘法和辅助变量法。
2.1 最小二乘法
首先给出模型类型,在该类型下确定系统模型的最优参数。这种具有格式规范的辨识方法可以演绎成递推形式。递推的最小二乘算法计算量小,可以用于在线辨识,即使辨识对象随时间发生变化,模型也可以对其进行跟踪,不断地进行更新和修正辨识参数,从而成为一种被广泛采用的辨识方法。
应用最小二乘法对系统模型参数进行辨识的方法有离线辨识和在线辨识两种[6]。离线辨识是在采集到所需全部输入输出数据后,用最小二乘法对数据集中处理,从而获得模型参数的估计值;而在线辨识是一种在系统运行过程中进行的递推的辨识方法,所应用的是实时采集的系统输入输出数据,应用递推算法对参数估计值进行不断修正,以取得更为准确的参数估计值。
2.2 辅助变量法
由于最小二乘估计是非一致的、有偏差的,为了克服它的缺点,形成了一些以最小二乘法为基础的辨识方法:广义最小二乘法(GLS)、辅助变量法(IVA)和增广矩阵法(EM),以及将一般的最小二乘法与其他方法相结合的方法[7]。辅助变量法是很有使用价值的辨识方法,尤其当噪声是有色的,而噪声的模型结构又不好确定时,辅助变量法更能显示出它的优势[8]。
辅助模型辨识思想(auxiliary model identification idea)是借助于系统的可测信息,建立一个辅助模型,用辅助模型的输出代替系统的不可测变量的一种辨识方法[9]。它的基本思想是在辨识过程中设法构造一种新的变量信号,称这个信号变量为辅助变量。这个辅助变量的特点是它与过程误差是不相关的,但与过程中的有用信号则是相关的。利用这个相关法的思想,可以估计出模型的参数[10]。
3 系统辨识工具箱的简介
Matlab的系统辨识工具箱提供了进行系统辨识的有力工具[11]。系统辨识中的模型是考虑了噪声影响的随机模型[12]。MATLAB工具箱包括模型类和模型结构参数的确定两部分内容。利用MATLAB编程环境,开发图形界面和多种辨识模型与算法等[13]。模型类的确定主要是根据先验知识对过程的特性进行一定程度的假设,明确所要建立的模型是静态的还是动态的,是连续的还是离散的、是线性的还是非线性的、是参数模型还是非参数模型。支持的模型类主要有:非参数模型类中的脉冲响应模型;参数模型中的(ARX)模型、(ARMAX)模型、Box-Jenkins模型和状态空间模型等。在模型结构确定以后,就可以进行模型参数的辨识了,MATLAB中对模型进行参数辨识方法包括最小二乘法、误差预报估计法、辅助变量法、几何网络法等。基于最小二乘法[14],在MATLAB仿真环境下,待辨识模型的输入输出数据的导入如图1所示。
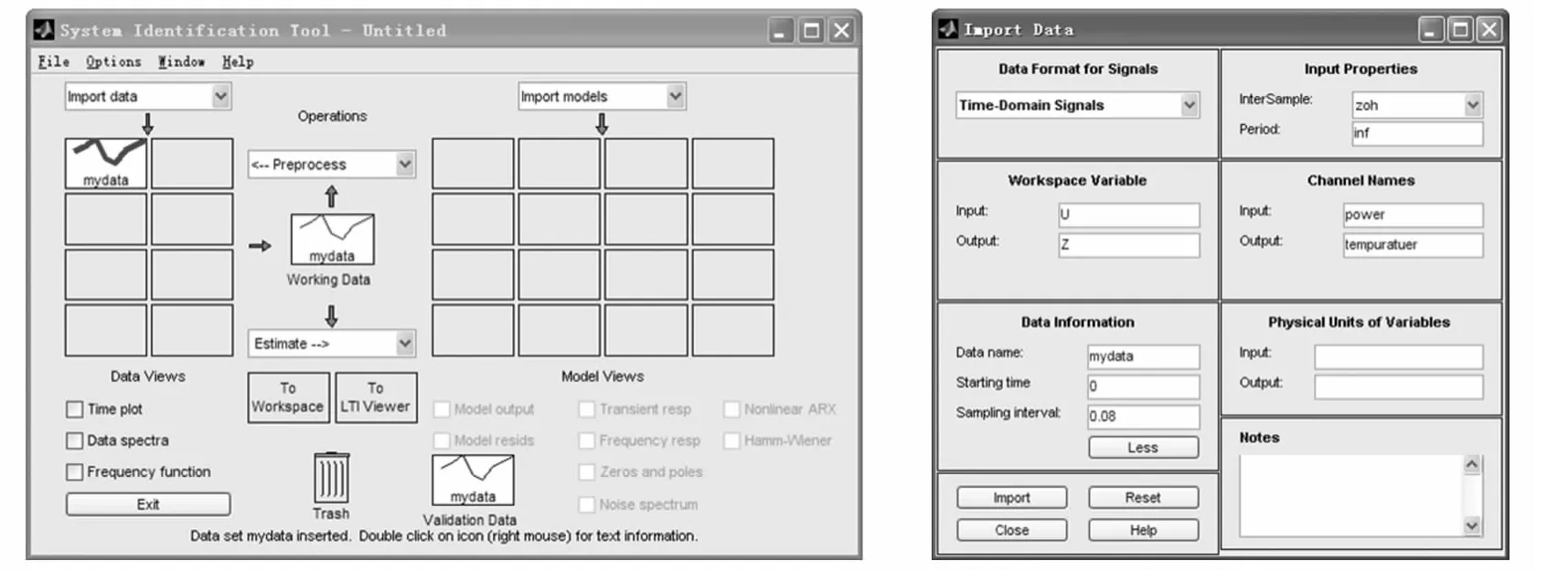
图1 数据的导入
工具箱中提供交互式的图形界面工具,能方便实现数据的预处理、模型类型的选择和参数估计以及模型验证和比较等功能[15]。
4 应用实例
4.1 待辨识实验数据
假设已知某实际系统在正弦信号作为输入情况下的响应如表1所示。
4.2 模型参数辨识
针对表1中的数据采用最小二乘法进行模型参数辨识,其中模型采用自回归各态经历(ARX)模型,如图2所示。经过估算得到传递函数如图3所示。

表1 系统输入输出数据
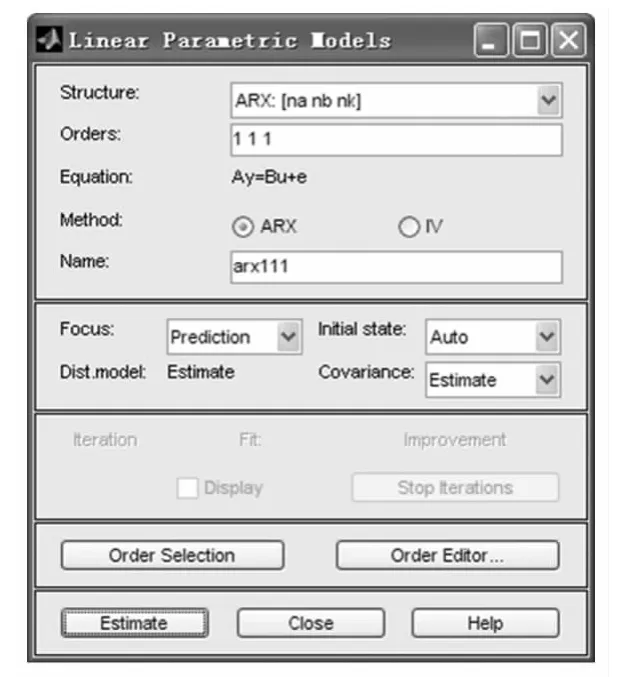
图2 最小二乘法辨识参数设定
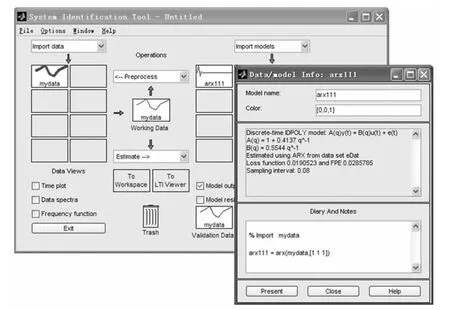
图3 最小二乘法辨识结果
所以得到的传递函数为:
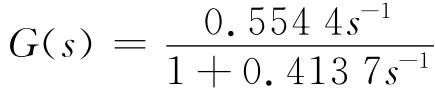
若针对表格中的数据采用近似最优4阶辅助变量法进行模型参数辨识,如图4所示。经过估算得到传递函数如图5所示。
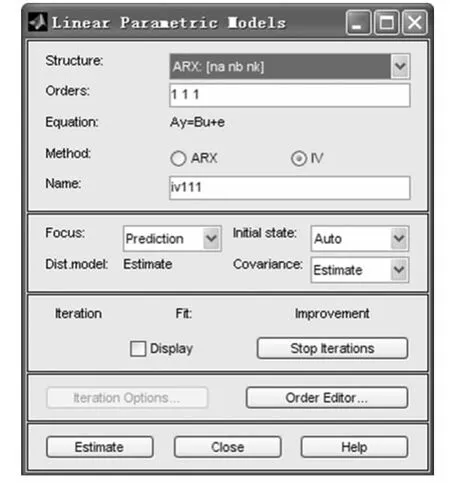
图4 近似最优4阶辅助变量法辨识参数设定
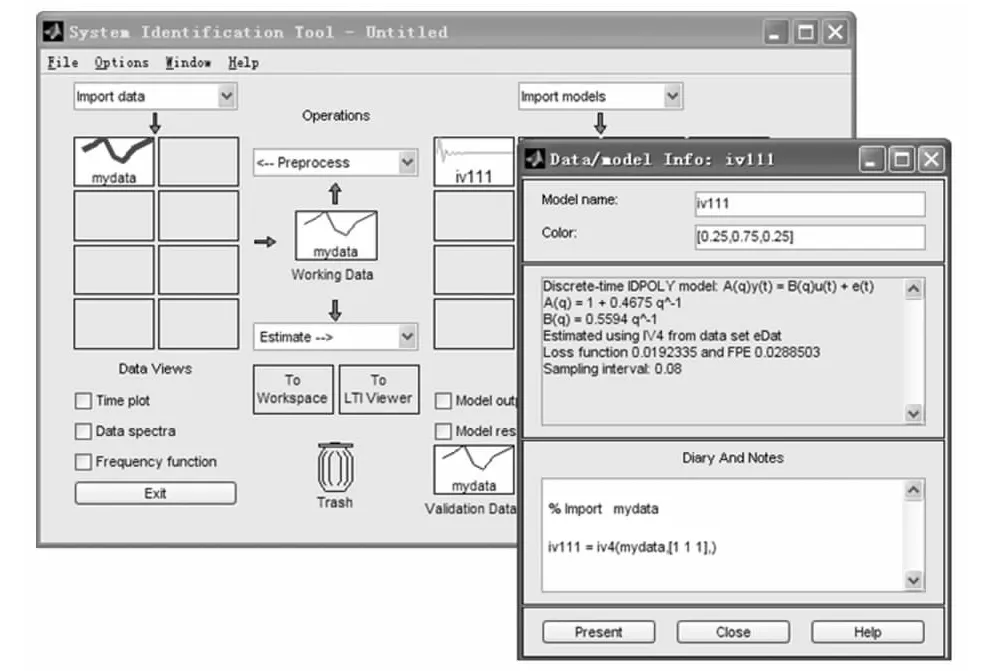
图5 近似最优4阶辅助变量法辨识结果
所以得到的传递函数为:
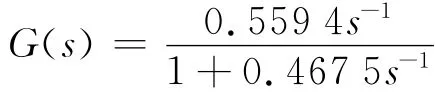
4.3 模型验证
经过两种方法的辨识得到的模型还要经过验证来证明其正确性。对两种模型和实验对象采取相同的输入信号,观察输出信号,如果模型输出和实际输出幅度拟合很好就说明模型的正确性。最小二乘法所得模型输出和实验对象输出对比如图6所示,近似最优4阶辅助变量法所得模型输出和实验对象输出对比如图7所示。
从图6和图7所示结果可见两种方法所得模型和实验对象有较好的拟合效果,较好地完成了模型的辨识。而近似最优4阶辅助变量法所得模型拟合精度高于最小二乘法所得模型。当噪声的模型结构不好确定时,最优4阶辅助变量法更显示出对系统辨识的优越性。而MATLAB系统辨识工具箱中提供了各种各样的系统辨识函数,为我们提供了一个可实现方便、快捷的系统建模方法。
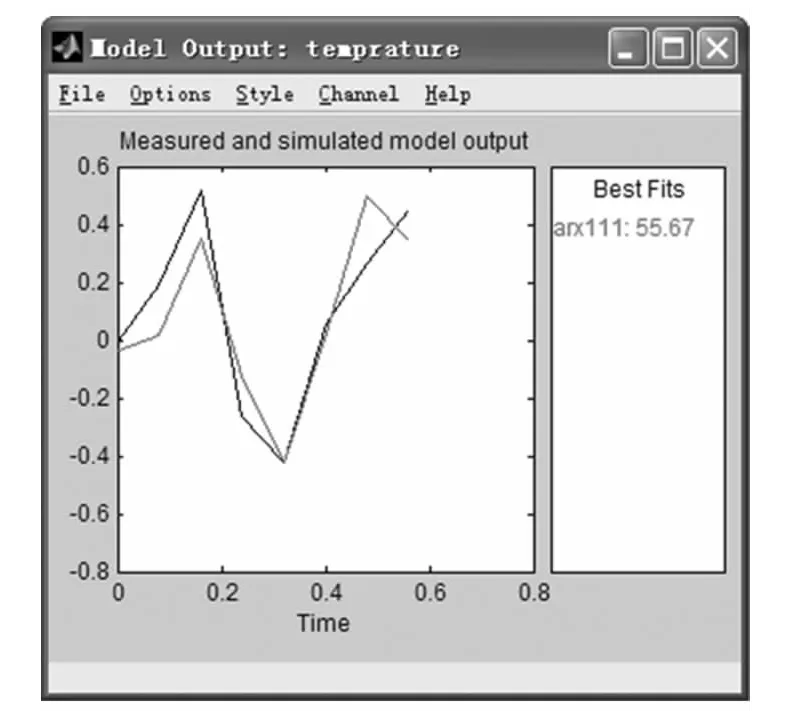
图6 最小二乘法辨识曲线拟合
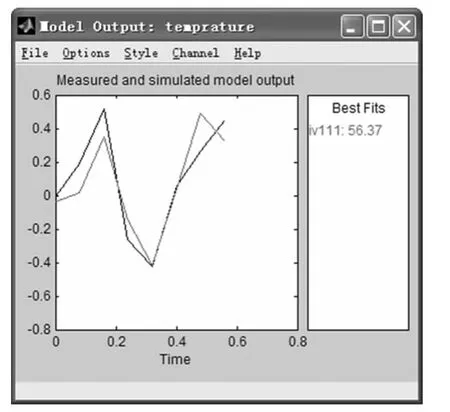
图7 近似最优4阶辅助变量法辨识曲线拟合
[1]郭利辉,朱励洪.基于 MATLAB的最小二乘法系统辨识与仿真[J].许昌学院学报,2010,29(2):24-27.
[2]陈杰,朱琳.基于混合最小二乘支持向量机网络模型的非线性系统辨识[J].控制理论与应用,2010,27(3):303-309.
[3]吕秋霞,李继容.Matlab在系统辨识中的应用[J].仪器仪表用户,2008,28(3):60-61.
[4]ZADEH L A.From circuit theory to system theory[J].Proc IRE,1962,50(5):856-865.
[5]郑剑翔.MATLAB系统辨识工具箱在系统控制设计中的应用[J].福州大学学报:自然科学版,2010,38(5):703-707.
[6]刘静纨.最小二乘法在系统辨识中的应用[J].北京建筑工程学院学报,2004,20(3):19-22.
[7]王琳,马平.系统辨识方法综述[J].电力情报,2011,63(4):63-66.
[8]鲁照权,胡焱东.具有限定记忆的辅助变量参数辨识法与仿真研究[J].系统仿真技术,2009,5(2):105-121.
[9]丁峰.系统辨识(4):辅助模型辨识思想与方法[J].南京信息工程大学学报:自然科学版,2011,3(4):289-318.
[10]严晓久,周爱国.基于辅助变量法的系统参数辨识[J].计算机应用与软件,2004,21(7):127-129.
[11]史贤俊,廖剑.基于 MATLAB的广义最小二乘参数辨识与仿真[J].计算机与数字工程,2009(8):173-175.
[12]郑征,田书.基于 MATLAB的辅助变量法参数辨识与仿真[J].机床与液压,2006(12):180-184.
[13]倪博溢,萧德云.MATLAB环境下的系统辨识仿真工具箱[J].系统仿真学报,2006,18(6):1493-1496.
[14]李颖,林洪生.基于相对误差的曲线最小二乘拟合[J].沈阳师范大学学报:自然科学版,2012,30(3):338-342.
[15]齐晓慧,田庆民.基于 Matlab系统辨识工具箱的系统建模[J].软件开发与应用,2006,25(10):88-90.

