最小二乘支持向量机在API预测中的应用

柳 春，李四海，魏邦龙

（1.甘肃中医学院 信息工程学院，兰州 730000；2.兰州城市学院 信息工程学院，兰州 730070）

0 引 言

近年来，小波分析及BP神经网络被广泛应用于大气污染物浓度时间序列的分析和预测。通过对空气污染指数时间序列进行连续小波变换，依据小波模极大值理论，可以发现序列的长期趋势性及局部波动性和随机性［1］。BP神经网络［2］具有很强的自学习及非线性映射能力，可用于建立气象因子与大气污染物SO2、NOx、可吸入颗粒物PM10等之间的非线性映射［3－6］。但是单纯以气象因子作为网络输入，并没有很好地挖掘时间序列本身的有用信息，导致在时间序列非平稳阶段的预测精度不高，并且由于BP网络本身采用梯度下降学习算法，容易陷入局部极小，网络的训练误差和泛化能力无法很好地平衡，这些问题将导致使用BP网络预测污染物浓度时其结果并不稳定。

LS－SVM是建立在标准支持向量机之上的一种小样本机器学习方法，具有坚实的理论基础，能够在经验风险和结构风险之间取得平衡，泛化能力好，预测结果稳定。首先使用小波分解充分挖掘时间序列本身的趋势性和波动性信息，提取时间序列在不同小波尺度下的高低频信息；然后以各尺度上的小波系数单支重构序列和重要的气象因子作为最小二乘支持向量机的输入，对兰州地区的空气污染指数进行实例预报，结果显示，该模型在预测精度及稳定性方面均明显好于传统的BP神经网络。

1 影响空气污染指数的气象因子

兰州位于青藏高原东北边缘，地处南北两山夹峙之中，市区海拔1 518m，两山相对高度300～600 m，构成哑铃型河谷盆底，特殊的地形条件使其一直以来空气污染严重，主要原因在于低空脱地逆温和贴地逆温年发生频率高、贴地逆温层厚度年均564m，脱地逆温层底的年均相对高度为1 527m，这对空气污染物的扩散产生不利影响［7］。

研究表明［8］，静风、逆温是构成兰州大气污染的基础原因。空气污染指数通常是根据SO2、NO2、PM10的浓度计算得出，这3种污染物浓度与平均风速、平均温度呈负相关，与相对湿度呈正相关［9］。

2 相关理论

2.1 离散小波变换

小波分析是通过一个基本小波的伸缩和平移构成一系列小波函数用于对信号进行多尺度逼近和分析。小波变换具有良好的时频局部化能力，信号在小波域上将被分解为任意系列频带的直和，小波变换享有信号处理的“数学显微镜”美誉。小波具有许多良好的性质，如消失矩、正交性等，小波变换主要用于信号去噪、信号压缩及特征抽取。离散小波变换在处理波动性较大的离散序列时十分有效［10］。

设信号f（t）在Vj空间中的离散采样序列为f（k），k＝0，1，2，…，n－1，则 Mallat小波分解算法为：

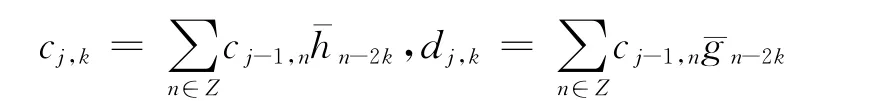
其中，和分别为信号的低频和高频部分，h（n）和g（n）分别为低通滤波器H和高通滤波器G的系数，且

Mallat重构算法为：

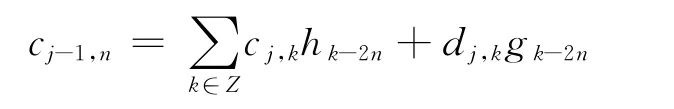
2.2 LS－SVM回归

LS－SVM是Suykens等人在标准支持向量机的基础上提出的一种机器学习方法，通过将标准支持向量机中的损失函数设为误差的二次项，将不等式约束设为等式约束后，将二次规划问题转化为求解线性KKT方程组，这样就降低了参数优化的难度，提高了模型的适应性和精度，拓展了支持向量机的应用空间［11－12］。

设训练样本为：

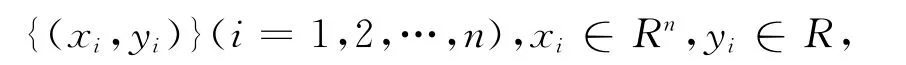
通过非线性映射函数φ（·）将样本映射到高维特征空间进行线性回归：

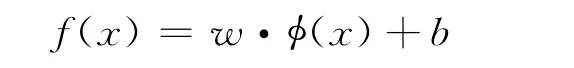
其中，w为权值向量，b为偏置量。

根据结构风险最小化原则，并注意到最小二乘支持向量机的损失函数为误差ξ的二次项，故优化问题为：

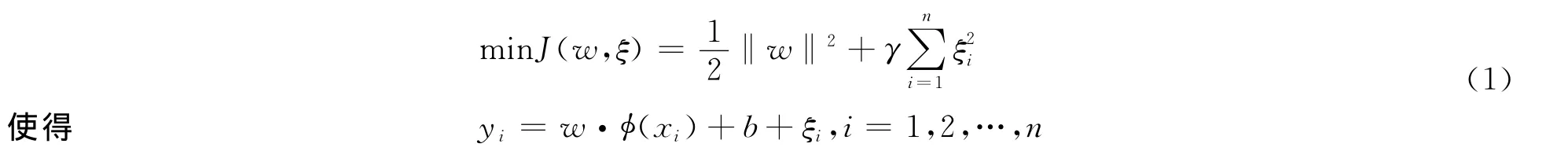
其中，γ为正则化参数。使用拉格朗日乘子法将上述问题转化为无约束对偶空间优化问题并根据优化条件，可得：

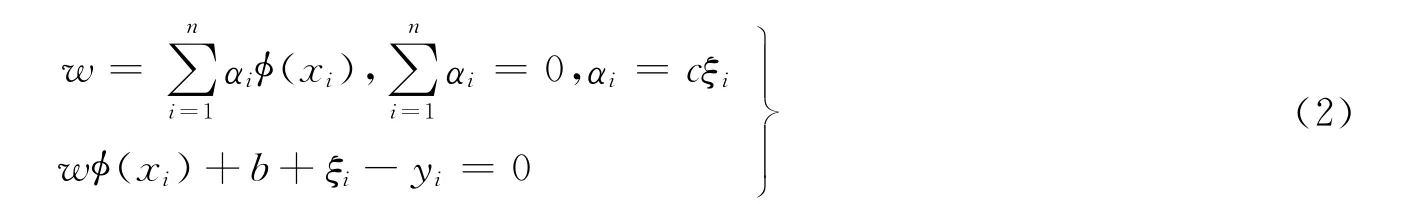
根据 Mercer条件，定义核函数：K（xi，xj）＝φ（xi）·φ（xj）。

将式（2）的优化问题转化为求解线性方程组：

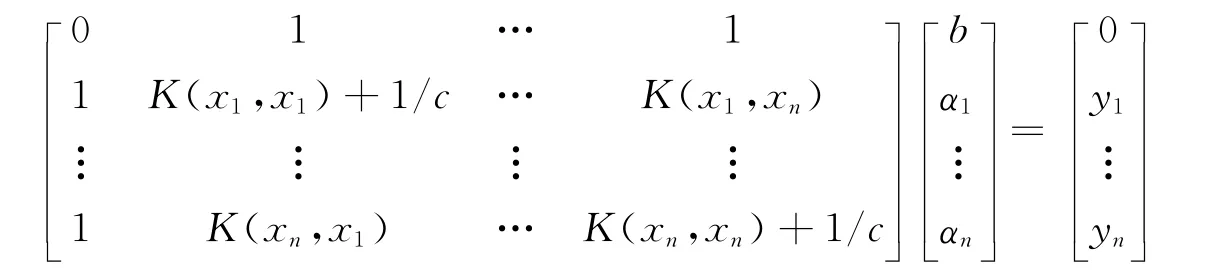
最后得到LS－SVM回归方程为：

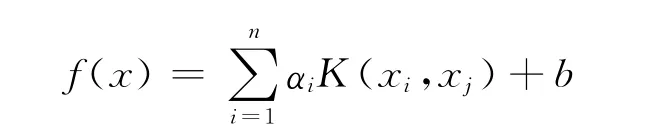
常用的核函数有径向基核函数：

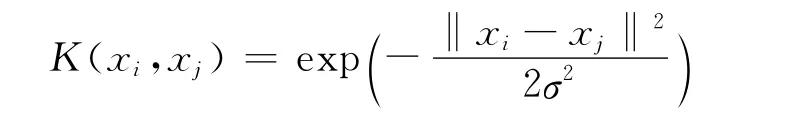
3 LS－SVM预报模型

3.1 小波特征提取

选用db3小波，使用Matlab R2009中的小波工具箱对2011－04－21—2012－04－20的兰州地区空气污染指数序列进行三层小波分解，根据分解得到的小波系数对原始信号进行单支重构，得到原始序列的单支重构序列｛a3，d3，d2，d1｝，其中a3为低频子序列，是原始序列的近似，反映了空气污染指数的长期变化趋势；d3，d2，d1是高频子序列，是原始序列的细节，反映了空气污染指数在不同“焦距”下的波动性。小波分解的结果如图1所示。

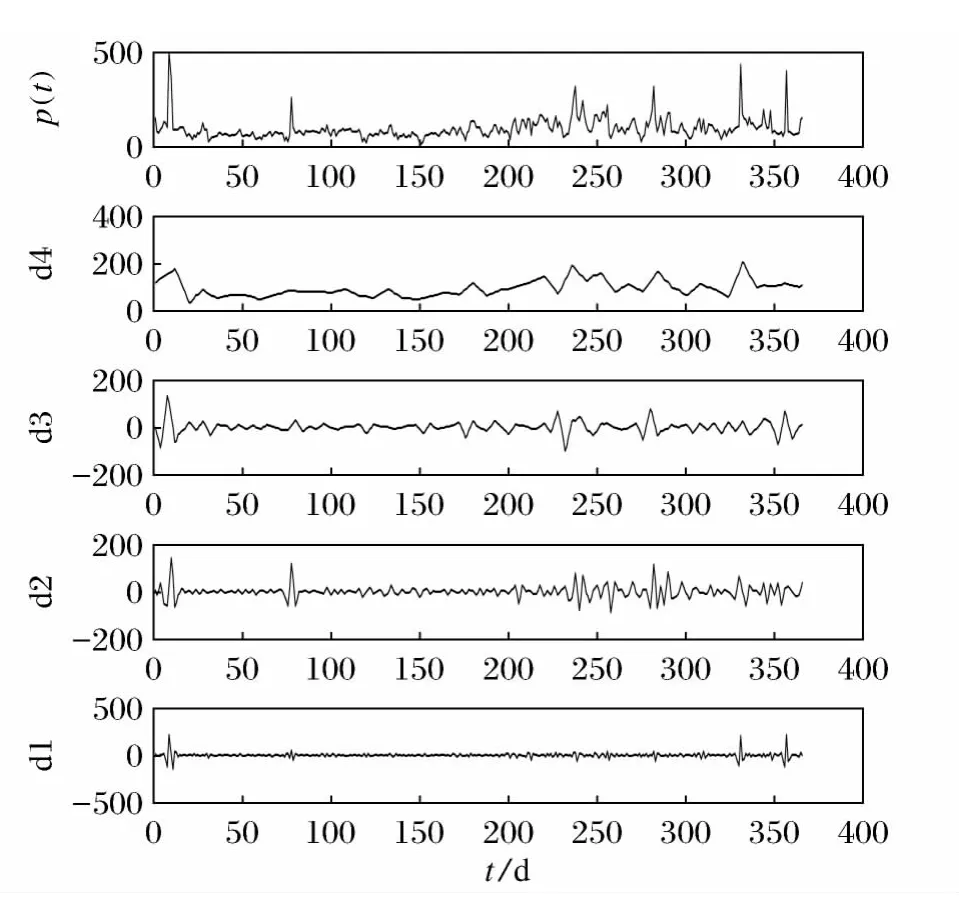
图1 原始时间序列的小波分解

3.2 模型结构

取2011－04－21—2012－04－20气象数据中的前一日空气污染指数、最高温度、最低温度、平均风速、相对湿度及小波单支重构序列｛a3，d3，d2，d1｝作为最终输入，共9个输入，以空气污染指数为最终输出，模型结构如图2所示。

3.3 模型训练和仿真

实验平台为 LSSVMlabv1＿8［13］及 Matlab R2009，核函数选用径向基核函数。2011－04－21—2012－04－20日的数据作为训练样本，训练样本的输入X为366×9矩阵，输出Y为366×1向量，将数据按维度归一化至［－1，1］。

基于径向基核函数的LS－SVM的预测性能与正则化参数γ及核函数宽度σ密切相关，参数优化方法主要有网格搜索法、遗传算法及粒子群算法。本文使用网格搜索法进行参数寻优，具体流程如图3所示。

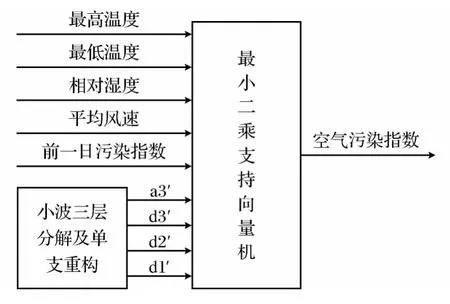
图2 LS－SVM结构图

经过网格搜索法寻优后，得到最优的γ＝740，σ＝20，建立并训练LS－SVM模型。部分代码如下：

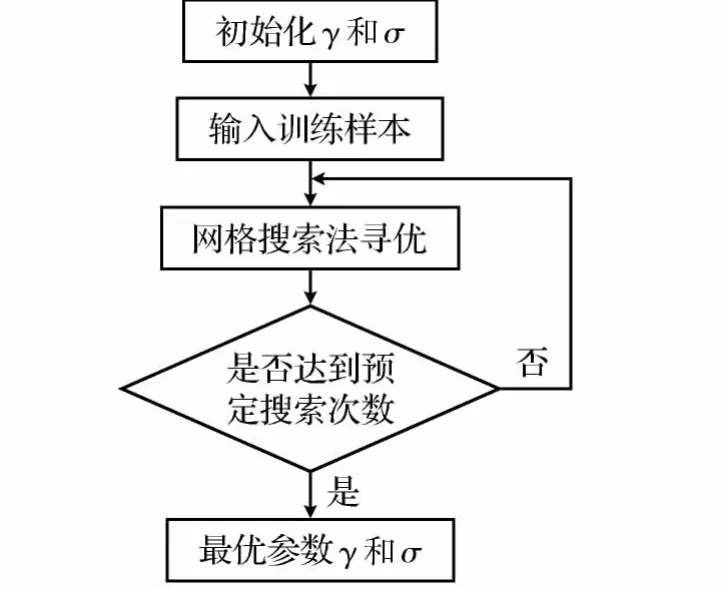
图3 网格搜索法对LS－SVM参数寻优流程图

将2012－04－21—06－17日的58个样本作为测试样本，使用LS－SVM模型进行测试，测试结果如图4所示。

由于特殊的地形条件，兰州地区的空气污染冬重夏轻的特点明显，且由于春季多出现浮尘天气，往往伴随春季污染指数的次高峰。从图4可以看出，2012－04－21—04－30日污染指数波动较大，其余阶段较为平稳。分析该阶段的气象因素，由于自23日凌晨起兰州地区出现首次区域性沙尘暴天气，致使连续几天污染指数较高，到27日凌时污染指数到达250，为重度污染。自5月开始，污染指数逐步进入平稳阶段。

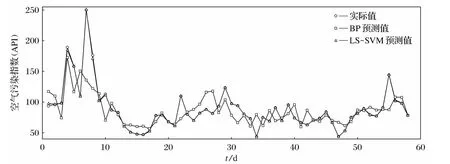
图4 LS－SVM和BP网络测试结果对比

从LS－SVM的预测精度看，对58个点的精度都很高，最大相对误差仅为3.66%。从稳定性来看，LS－SVM的稳定性相当好，连续运行多次，结果不会发生变化。原因在于LS－SVM通过对训练样本的学习，能够得到一组稳定、最优的训练样本参数αi及偏置量b，通过这些参数及训练样本能够得到未知样本与给定参数相对应的预测结果。

为进一步比较验证LS－SVM模型的优越性，建立了BP神经网络的预测模型。以最高温度、最低温度、平均风速、相对湿度4个气象因子及前一日污染指数作为输入，网络结构为5－13－1，各层传递函数为sigmoid函数，采用traingdx算法进行学习，误差设为0.001，学习率lr＝0.015。使用训练好的BP网络对相同的58个测试样本进行预测，两种模型的测试结果对比如图4所示。

对比发现，LS－SVM模型能够准确反映序列的总体变化趋势，BP网络仅能反映序列在平稳阶段的变化趋势。对比两种模型的预测精度，BP神经网络预测精度较好的阶段集中在时间序列的平稳阶段，但在时间序列波动较大的阶段，预测精度较差，这是由于网络需要设置的参数较多且最佳隐层单元数不易确定，模型推广能力不高，稳定性不好，更重要的原因在于没有充分挖掘有限样本中的趋势性及波动性信息，输入中缺少序列本身的变化信息。LS－SVM模型的输入中包含原始序列的低频及高频信息，低频序列能够表现空气污染指数序列的长期变化趋势，各尺度上的高频子序列则反映了空气污染指数序列的波动性，从模型结构分析，由于LS－SVM模型只需根据训练样本对正则化参数γ及核函数宽度σ进行寻优，参数设置少，模型使用简单。综合来看，LS－SVM模型预测精度高，泛化能力好、稳定性高。将两种模型各连续运行100次，表1对比了两种模型的性能，其中MAE为平均绝对误差，MSE为均方误差。从表1可以看出，与BP神经网络相比，LS－SVM模型具有更高的预测精度及更好的稳定性。

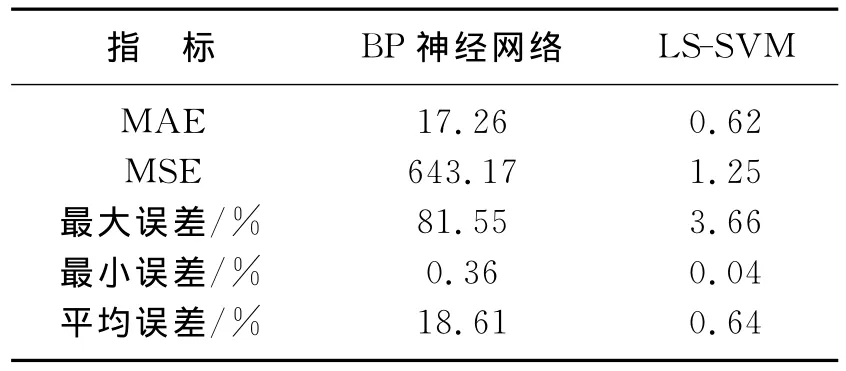
表1 BP神经网络和LS－SVM仿真结果对比

4 结 论

本文基于BP神经网络预测空气污染指数时在时间序列的非平稳阶段预测精度低、网络收敛速度慢且泛化能力较差，提出了LS－SVM预测模型并对模型参数进行了寻优。通过对空气污染指数的仿真实验，表明该模型对空气污染指数的所有阶段均具有较高的预测精度和稳定性，将该模型用于空气污染指数预报是可行的。基于改进的支持向量机及各种智能算法对正则化参数γ和核函数宽度σ进行优化［14－17］，进一步提高LS－SVM模型的预测精度及稳定性将是下一步的研究方向。

［1］王海鹏.基于小波变换的兰州市近十年空气污染指数变化［J］.环境科学学报，2011，31（5）：1071－1076.

［2］邹丽娜，丁茜.基于BP算法的成绩预测模型［J］.沈阳师范大学学报：自然科学版 ，2011，29（2）：226－229.

［3］郭庆春，何振芳，寇立群，等.BP神经网络在北京市 API预报中的应用［J］.环境工程，2011，29（4）：106－108.

［4］王俭，胡筱敏，郑龙熙，等.基于BP模型的大气污染预报方法的研究［J］.环境科学研究，2002，15（5）：62－64.

［5］张静，李旭祥，许先意，等.大气环境数据分析预测方法对比研究［J］.中国环境监测，2010，26（6）：66－70.

［6］王芳，程水源，李明君，等.遗传算法优化神经网络用于大气污染预报［J］.北京工业大学学报：自然科学版，2009，35（9）：1230－1234.

［7］姜大膀，王式功，郎咸梅，等.兰州市区低空大气温度层结特征及其与空气污染的关系［J］.兰州大学学报：自然科学版，2001，37（4）：133－139.

［8］高建华.兰州市大气污染规律及治理对策［J］.西安石油学院学报：自然科学版，2003，18（4）：85－88.

［9］周秀杰，苏小红，袁美英.基于BP网络的空气污染指数预报研究［J］.哈尔滨工业大学学报，2004，36（5）：582－585.

［10］王西锋，高岭，张晓孪.基于小波技术的网络流量分析和预测［J］.计算机应用与软件，2008，25（8）：70－72.

［11］周子英，段建南，李萍，等.基于最小二乘支持向量机的耕地面积预测研究［J］.计算机应用研究，2012，29（3）：873－876.

［12］李文莉，李郁侠.基于粒子群最小二乘支持向量机的水文预测［J］.计算机应用，2012，32（4）：1188－1190.

［13］BRABANTER K D，KARSMAKERS P，OJEDA F，ALZATE C，et al.LS－SVMlab Toolbox User's Guide［EB／OL］.［2011－08－09］.http：∥www.esat.kuleuven.be／sista／lssvmlab.

［14］张豪，罗亦泳，张立亭，等.基于遗传算法最小二乘支持向量机的耕地变换预测［J］.农业工程学报，2009，25（7）：226－231.

［15］杨红，罗飞，许玉格，等.基于混沌优化的LS－SVM 非线性预测控制方法［J］.计算机工程与应用，2010，46（5）：229－232.

［16］徐勇，张广辉，钱锋.基于改进克隆选择算法的最小二乘支持向量机［J］.华东理工大学学报：自然科学版，2008，34（5）：729－733.

［17］毛晓娟，何小阳，温伟峰.一种改进的最小二乘支持向量机软测量建模方法［J］.自动化仪表，2011，32（5）：39－45.