高等数学中的辅助函数设计

成丽波，刘振文

（长春理工大学 理学院，长春 130022）

0 引 言

辅助函数即是辅助解决问题所用的函数，构造辅助函数的方法是在讲授一元函数微分中值定理之后出现的一种重要方法，在文献［1－10］中从不同角度进行了论述，文献［11－13］对于微分中值定理证明中关于辅助函数的做法也进行了讨论。微分中值定理［14－15］的理解和应用是教学中的难点，因此如何应用中值定理证明一些问题也给一些教师和学生带来不少困惑，本文通过例子总结一下在教学过程中做辅助函数的一些体会，希望能引起同行的共鸣。

1 关于利用微分中值定理证明问题中辅助函数的做法

微分中值定理是Rolle定理、Lagrange中值定理、Cauchy中值定理和Taylor定理的统称，这几个定理的核心是Lagrange中值定理，证明过程都是以Rolle定理为基础，适当构造满足Rolle定理条件的辅助函数，使中值定理成为一个整体。本段介绍如何构造适当的辅助函数，利用中值定理完成证明过程中的一些题。

首先，Rolle定理适合于证明导数在个别点ξ处的值为等式的问题，即在ξ点处使得F′（ξ）＝0的问题。解决这类问题的关键是找到这个辅助函数（即原函数）F（x），使其满足Rolle定理的3个条件，则有F′（ξ）＝0成立，需要注意的是有些问题还需要寻找满足定理条件的闭区间。下面作者给出几个具体例子，介绍用逆推法观察得到辅助函数（原函数）和利用不定积分求出辅助函数（原函数）的方法。

例1 设f（x）在［0，1］上连续，在（0，1）内可导，且证明存在ξ∈（0，1），使

分析 题目中是要证明某个函数的导数在个别点ξ处的值为等式的问题，可以考虑用Rolle定理解决。即找到一个辅助函数F（x），使得ξ是F′（x）＝0的根，亦即F′（ξ）＝0，因此找辅助函数F（x）就是解决此问题的关键。从结论入手开始逆推：要证明ξ是F′（x）＝f′（x）－1＝0的根，也就是要找到函数F（x）在某个闭区间［a，b］上满足Rolle定理条件，且使F′（x）＝f′（x）－1，由求导法则很容易观察出F（x）＝f（x）－x，需要注意这个函数满足Rolle定理条件的区间并不是题目给定的闭区间［0，1］，因此，还需要寻找新的闭区间，通常情况下此区间的端点应该在题目给定的闭区间［0，1］上，可通过闭区间上连续函数的性质定理得到此区间的端点。由于F（x）＝f（x）－x在［0，1］上连续，且所以可由闭区间上连续函数的介值定理找到一点这样对F（x）在闭区间［0，x］上应用Rolle定理问题就可以顺0利解决了。详细证明过程如下：

证明 作辅助函数F（x）＝f（x）－x，由已知条件可知F（x）＝f（x）－x在［0，1］上连续，又因为利用闭区间上连续函数的介值定理知至少存在一点使F（x）＝0，又F（0）＝0，因此F（x）在［0，x］上满足Rolle定理的00条件，故至少存在一点ξ∈（0，x0）⊂（0，1），使得F′（ξ）＝0，即f′（ξ）＝1。证毕。

如果在寻找辅助函数（原函数）时不容易直接观察得到，也可以通过不定积分法求得原函数，就是所要寻找的辅助函数，如下例所示。

例2 假设f（x）和g（x）在［a，b］上存在二阶导数，并且g″（x）≠0，在（a，b）内g（x）≠0，证明在（a，b）内至少存在一点ξ，使

分析 本题同样可考虑使用Rolle定理。要证明ξ是的根，因此，需要寻找辅助函数（原函数）F（x），使

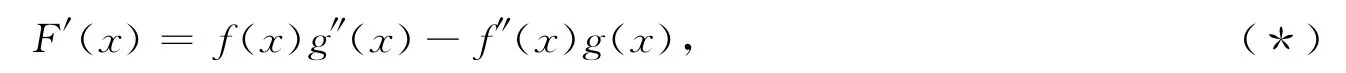
此题不同于例1能直接观察出原函数，所以可通过求不定积分得到原函数F（x）。因此将式（＊）两端同时求不定积分得

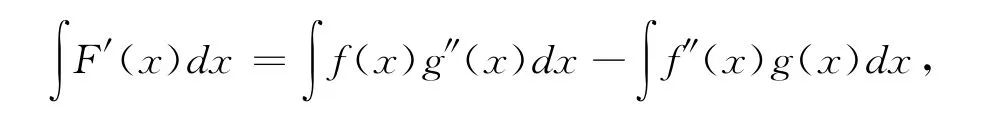
再利用分部积分法可知

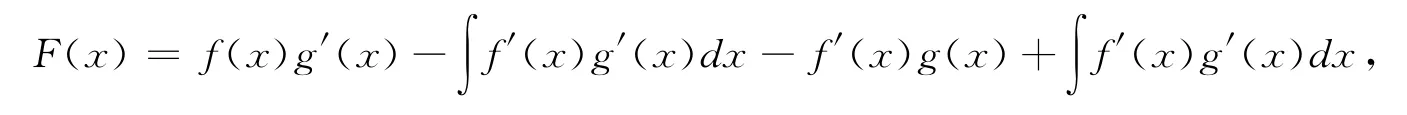
因此F（x）＝f（x）g′（x）－f′（x）g（x），再由Rolle定理即可解决问题。证明过程如下：

证明 设辅助函数F（x）＝f（x）g′（x）－f′（x）g（x），由已知条件可知F（x）在［a，b］上连续，在（a，b）内可导，且F（a）＝f（a）g′（a）－f′（a）g（a）＝0，F（b）＝f（b）g′（b）－f′（b）g（b）＝0。

由Rolle定理知在（a，b）内至少存在一点ξ，使F′（ξ）＝0，即f（ξ）g″（ξ）－f″（ξ）g（ξ）＝0，又因为证毕。

以上2例都是从结论入手采用逆推法寻找辅助函数，但有时也可从已知条件入手采用正推法，再结合积分上限函数作辅助函数也是比较方便的，下举一例。

例3 设f（x）在［0，π］上连续，且试证在（0，π）内至少存在2个不同点ξ1和ξ2，使得f（ξ1）＝f（ξ2）。

分析 与例1和例2类似知此题可考虑用Rolle定理解决，但是如果采用前2例的方法很难做出辅助函数，知道积分上限函数是被积函数的原函数，结合已知条件启发考虑函数作为辅助函数，再通过与例1类似的方法找出使Rolle定理条件成立的闭区间，2次使用Rolle定理即可得出所要求的2个不同点ξ1和ξ2，使F′（ξ1）＝0，F′（ξ2）＝0，这样f（ξ1）＝f（ξ2）成立。证明过程如下：

在讨论代数方程根的唯一性问题中也可以涉及到引入辅助函数的方法，请看以下例子：

例4 证明方程x3＋x－1＝0在（0，1）内只有一个实根。

分析 此类问题通常考虑两个方面，即根的存在性和唯一性。存在性往往需要做一个在［0，1］上连续的辅助函数，一般可将方程的一端作为辅助函数，利用连续函数的介值定理说明根的存在性；唯一性可用反证法或单调性加以说明即可。证明过程如下：

证明 先证存在性.做辅助函数F（x）＝x3＋x－1，则因F（x）在［0，1］上连续，且F（0）＝－1＜0，F（1）＝1＞0，故由连续函数的介值定理知方程在（0，1）内至少有一个实根；

再证唯一性，采用反证法：假设方程在（0，1）内有两个不同的实根x1，x2（不妨设x1＜x2），即F（x1）＝F（x2）＝0，对F（x）在［0，1］上应用Rolle定理即知必存在一点ξ∈（x1，x2）⊂（0，1），使F′（ξ）＝3ξ2＋1＝0，这在实数域上是不可能的，所以方程在（0，1）内只有一个实根。证毕。

2 关于不等式证明问题中辅助函数的做法

不等式的证明是微积分中的常见问题之一，运用单调性及Lagrange中值定理结合辅助函数是比较常用的方法。在利用单调性证明不等式问题中，通常情况下是将不等式两边相减之后的函数作为辅助函数，请考虑如下例题。

例5 设x∈（0，1），证明不等式成立。

分析 因x∈（0，1），故1－x＞0，于是所证的不等式变为（1－x）e2x＜1＋x，所以可对f（x）＝（1－x）e2x－（1＋x）利用单调性得到结论。证明过程如下：

证明 设辅助函数f（x）＝（1－x）e2x－（1＋x），x∈（0，1），则由f′（x）＝（1－2x）e2x－1，f′（0）＝0，f″（x）＝－4xe2x＜0，得知f′（x）在（0，1）上单调减少，故在（0，1）内f′（x）＜0，从而f（x）在（0，1）上单调减少，再由f（0）＝0知在（0，1）内f（x）＜0，即（1－x）e2x－（1＋x）＜0，从而得证当x∈（0，1）时，成立。证毕。

利用Lagrange中值定理证明不等式也是比较常见的方法，解决这类问题一般采用逆推法，适当选取辅助函数，通过Lagrange中值定理中个别点ξ满足的不等关系可将问题解决。考虑如下例题：

例6 设a＞b＞0，证明

分析 因a＞b＞0，故a－b＞0，这样要证明的不等式可化为中间部分可由f（x）＝lnx在［b，a］上使用Lagrange中值定理得到，即再通过b＜ξ＜a即可得到结论。证明过程如下：

证明 设辅助函数f（x）＝lnx，则f（x）在［b，a］上连续，在（b，a）内可导，由Lagrange中值定理知至少存在一点ξ∈（b，a），使故而a－b＞0，所以即证毕。

3 结 语

本文谈到的关于辅助函数的做法是在教学过程中总结的一点体会，经过分析总结，学生很容易就能够接受这些问题。通过学习如何设计辅助函数，许多同学反映不再害怕利用中值定理作证明题这个拦路虎了，也达到了事半功倍的教学效果。

［1］李君士.两个微分中值定理证明中辅助函数的多种做法［J］.数学的实践与认识，2004，34（10）：166－169.

［2］刘文武.两个微分中值定理中辅助函数做法探讨［J］.数学的实践与认识，2005，35（8）：242－247.

［3］宋振云，陈少元，涂琼霞.微分中值定理中辅助函数的构造［J］.高师理科学刊，2009，29（2）：11－12.

［4］陈静，王来生，周志坚.浅析一元微积分学中的构造辅助函数法［J］.高等数学研究，2006，34（6）：28－29.

［5］刘勇.浅谈构造辅助函数的基本方法［J］.湖北广播电视大学学报，2009，29（4）：155－156.

［6］任树联.谈微分中值定理运用中辅助函数的构建［J］.长沙通信职业技术学院学报，2006，15（1）：103－107.

［7］陈志惠.根据微分中值公式构造辅助函数的3种类型及其方法［J］.沈阳工程学院学报：自然科学版，2008，10（2）：18－20.

［8］唐秋林，吴美云.数学分析中构造辅助函数的几种方法［J］.数学学习与研究，2012，17（8）：89－90.

［9］江婧，田芯安.在数学分析中做辅助函数解题［J］.重庆文理学院学报：自然科学版，2009，29（4）：17－21.

［10］李志飞.罗尔定理应用中辅助函数的构造［J］.高等数学研究，2006，34（5）：19－21.

［11］唐帅，王志华.微分中值定理中辅助函数的构造方法［J］.邵阳学院学报：自然科学版，2009，6（4）：26－30.

［12］左飞.例谈微分中值定理中辅助函数的构造方法［J］.科技信息，2008，24（7）：399－401.

［13］谭洁琦.浅谈微分中值定理中辅助函数的构造［J］.四川教育学院学报，2008，24（7）：101－103.

［14］同济大学数学系.高等数学［M］.6版.北京：高等教育出版社，2007：128－154.

［15］四川大学数学学院高等数学教研室.高等数学［M］.4版.北京：高等教育出版社，2009：140－188.