具有学习效应且加工时间可控的单机排序问题

王 方，赵传立

（沈阳师范大学 数学与系统科学学院，沈阳 110034）

带有可控加工时间的排序问题［1－10］，自1980年以来备受关注，并取得了许多研究成果。本文将学习效应与可控加工时间相结合，拓展了文献［7］的主要结果。问题可描述如下。

设有n个相互独立的工件的集合，记为｛J1，J2，…，Jn｝，工件在0时都已到达，且加工过程中中断不被允许。工件J［j］的正常加工时间为P［j］，需要确定工件的加工顺序、划分、工期和资源分配量，极小化一个包含加权总误工数、工期分派、最大完工时间，和总资源消耗的费用函数。即目标函数为以下形式：

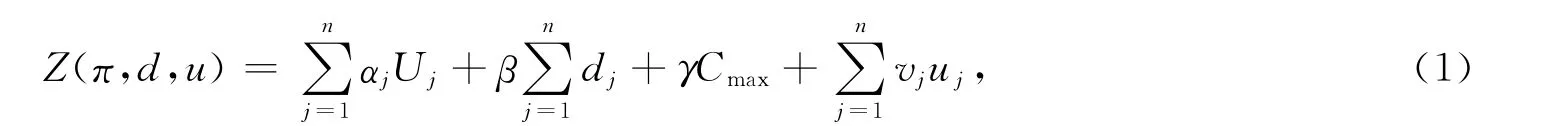
其中，Cj是工件Jj的完工时间是最大完工时间。Uj是工件Jj的延误指示变量，即当Cj＞dj时，置Uj＝1；否则，置Uj＝0，dj≥0是工件Jj的工期。αj是工件Jj的延误费用，非负参数α和β分别表示工期的单位费用和最大完工时间的费用。uj是分配到工件Jj上的资源量，vj是分配到工件Jj上的资源量的单位费用。

研究带有以下两种工期分派方法的问题。

1）CON型：共同工期分派方法。这里所有工件都分派一个共同工期，即dj＝d，j＝1，2，…，n

2）SLK型：松弛工期分派方法。这里所有工件都有一个相同的松弛时间，即dj＝pj＋slk，这里slk≥0是一个确定的变量。

文献［11］考虑了一种机器具有学习效应的模型，当工件Jj排在序列的第r个位置时，其实际加工时间为pj＝，aj≤0是一个与工件相关的学习指标。本文中工件Jj的实际加工时间为：

I线性资源消耗函数：

凸资源消耗函数：

式中，k是一个正的常数。

1 预备结论

容易验证，带有CON型和SLK型工期分派方法的加工时间为常量的排序问题中的某些结论，仍然可以推广到可控加工时间的情形。并且带有SLK型的问题与CON型类似，因此以下本文均以CON型为例讨论。

在CON型工期分派方法下，工件可以划分为2个相邻的集合：

1）集合E。这里所有工件的加工时间总和定义为工期d的值，且这里的工件都在它的工期前完工，故称E为提前工件集合。

2）集合T。这里所有工件都在它的工期后完工，故称T为延误工件集合。

引理1 在CON型工期分派方法下，存在一个最优排序，任意两个工件的加工过程之间都没有空闲时间，且第一个工件的开始时间为零。

文中带有［j］的下标均表示工件排在第j个位置。

引理2 存在一个最优排序，在CON型工期分派方法下，集合E排在集合T前。

2 线性资源消耗函数的解

在CON型工期分派方法下，当资源分配与工件所排位置确定后，工件的加工时间被固定，就简化为找最优划分τ＊和工期d，极小化这个问题已被文献［12］解决，并在O（n）时间内给出以下算法。

算法1：

步骤2 集合E排在T之前，并且每个集合内部的次序无关。

步骤3 最优工期为集合E的完工时间，即

由算法1可知，最优工期和工件的划分是由加工时间决定的。然而，当加工时间由式（2）和式（3）确定时，意味着最优工期和工件的划分还将与工件所排位置和分配的资源有关。

由于对任意一种给定的划分、排序和资源分配，相应的最优工期就可以确定，因此，以下这个问题旨在确定最优的划分、排序和资源分配。

对任意一个给定的划分和排序，目标函数式（1）可变形为：

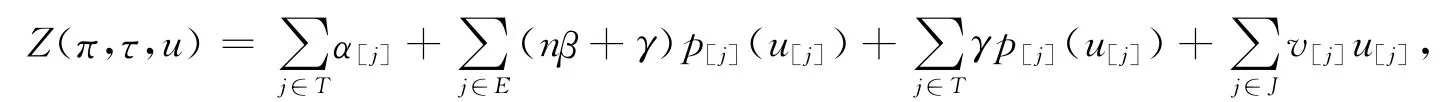
假定｜E｜＝l，｜T｜＝n－l.则上式又可变形为：

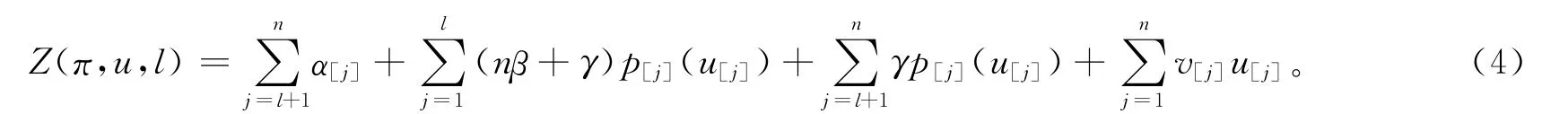
当加工时间为一个线性资源消耗函数式（2）时，目标函数式（4）变为：

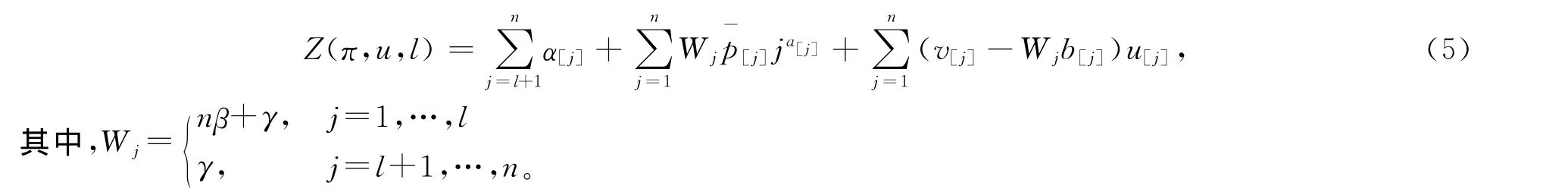
对于SLK型工期分派方法，带有固定加工时间的相关结论文献［8］中已做了详细分析。

引理3 在CON型工期分派方法下，对于任意给定的划分和工件序列，最优资源分配作为划分和工件序列的一个函数，可以这样得到：

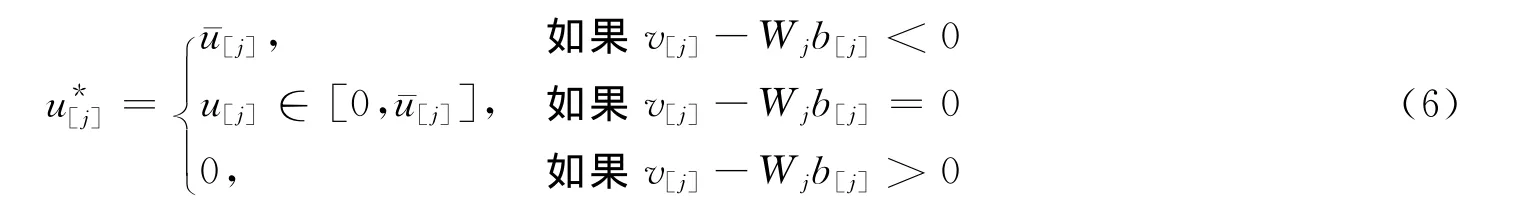
证明 对式（5）关于u［j］求导得证。

由以上分析可知，对于任意给定的划分和排序，最优资源分配都可以由引理3求出，那么，这个问题就简化为求一个最优划分和最优序列的排序问题。

然而，对于任意一个给定的划分，最优排序可以通过在O（n3）时间内解一个指派问题得到，分析如下：

根据前面在CON型工期分派方法下假定的划分，对于目标函数（5）式，当l给定时，令

其中，cij（l）依目标函数式（5）中Wj的不同而不同。

定义xij为一个0－1变量，当工件Ji排到第j个位置时，xij＝1；否则，xij＝0。对于目标函数式（5），指派问题可表示如下：

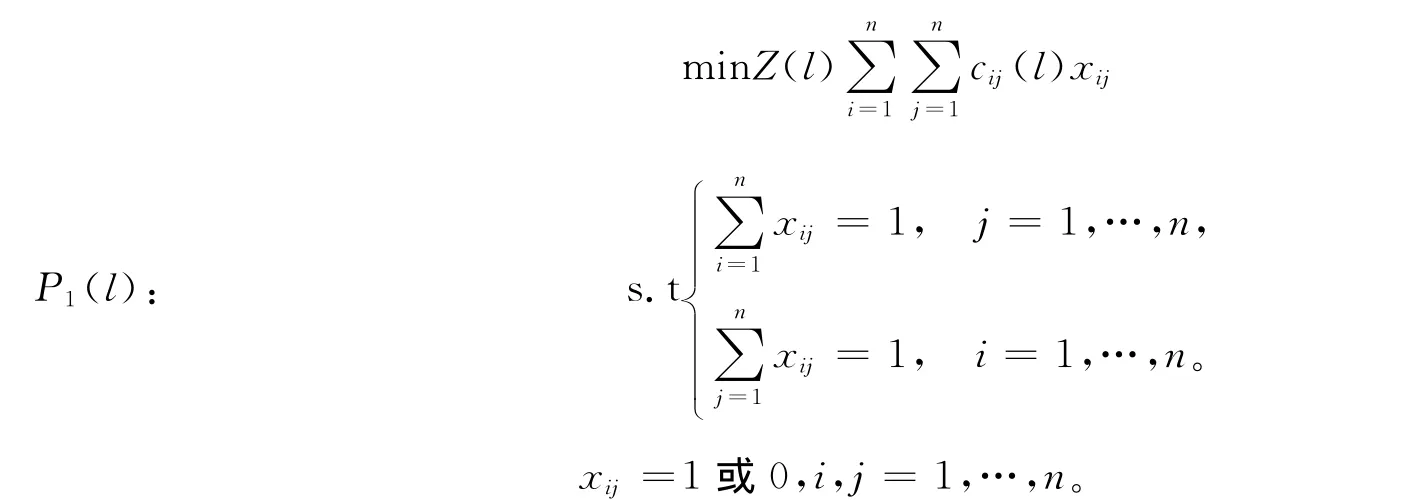
引理4 对于目标函数式（1），任意给定一种划分τ，在CON型工期分派方法下，当加工时间由式（2）确定时，相关最优排序可以通过解一个指派问题在O（n3）时间内得到。

根据以上的分析，对于任意一个给定的划分，都可以通过解指派问题找到最优排序。因此，这个问题又进一步简化为找最优划分τ＊的问题。

因为l的值有n种可能的取法，所以为了找最优的划分，只有取遍所有l可能值并解相应的l值对应的指派问题，才能得到这个问题的最优解。这个问题的最优解总结为算法2。

算法2 求解带有CON型工期分派方法的线性资源消耗函数最优解的算法。

初始 置Z＊＝∞，l＝0。

步骤1 当l≤n时：

步骤1.1 通过式（7）计算cij（l）的值；

步骤1.2 解指派问题P1（l）：，确定工件的最优排序π＊＝［1］，［2］，…，［n］和极小化费用Z（l）；

步骤1.3 如果Z（l）＜Z＊，那么，置Z＊＝Z（l），l＊＝l，π＊（l＊）＝π＊（l）；

步骤1.4l＝l＋1。

步骤2 当l＝l＊，π＊（l）＝π＊（l＊）时，通过引理3计算最优资源分配u＊（l），通过式（2）计算最优加工时间

定理1 算法2在O（n4）时间内解决了在CON型工期分派方法下，这个问题的目标函数为一个线性资源消耗函数时的最优解。

3 凸资源消耗函数的解

当加工时间为一个凸资源消耗函数式（3）时，代入式（4），则目标函数变为以下形式：

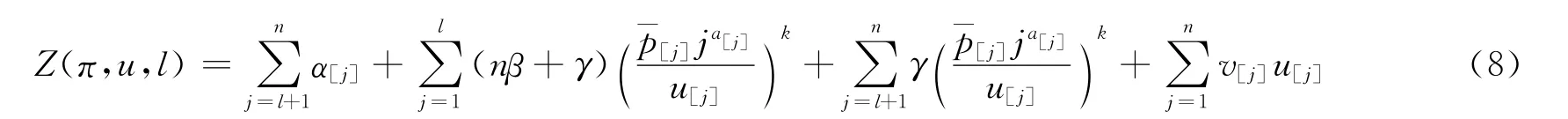
由目标函数式（8）可以看出，在CON型工期分派方法下，任意给定一种划分和排序，当加工时间为一个凸资源消耗函数时，这个问题变为一个关于资源分配的凸函数。因此，最优资源分配可描述如下：

引理5 最优资源分配u＊（π，l），作为划分和工件序列的一个函数，是：

CON型：

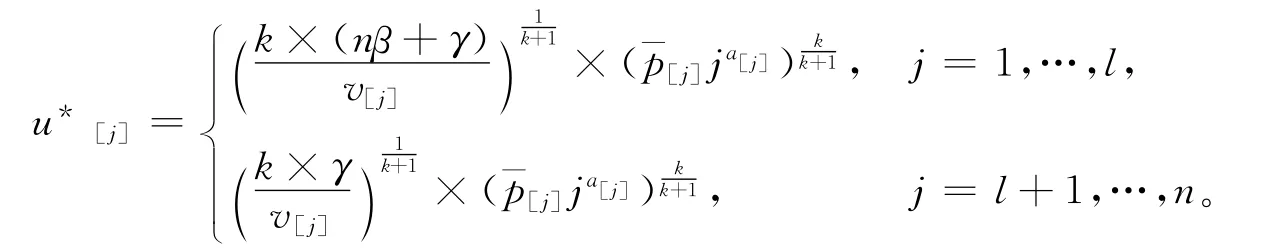
把引理5中的最优资源分配分别代入目标函数式（8），得到

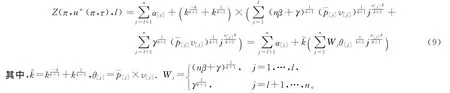
由于对于任意给定的划分和排序，最优资源分配都可以通过引理5得到。因此，这个问题又简化为找最优划分和排序的问题。

此时，任意给定的一种划分，最优排序仍然可以通过解指派问题，在O（n3）时间内得到。分析如下：

根据前面在CON型工期分派方法下假定的划分，对于目标函数式（7），当l给定时，令

其中，cij（l）依目标函数（9）式中Wj的不同而不同。

定义xij为一个0－1变量，当工件Ji排到第j个位置时，xij＝1；否则，xij＝0。对于目标函数（9）式，指派问题的表示同前面P1（t）的形式，不妨记为P2（t）。

引理6 对于这个问题，任意给定一种划分τ，在CON型工期分派方法下，当加工时间由式（3）确定时，相关最优排序可以通过解一个指派问题在O（n3）时间内得到。

由以上的分析，有下面的结论

对于任意一个给定的划分，都可以通过解指派问题找到最优排序。因此，这个问题的最优解又进一步简化为找最优划分τ＊的问题。

同样，因为l的值有n种可能的取法，只有取遍的所有l的可能值并解相应的l值对应的指派问题，才能得到这个问题的最优解。因此，当加工时间为一个凸资源消耗函数时，在CON型工期分派方法下，这个问题的最优解总结为算法3。

算法3 求解带有CON型工期分派方法的凸资源消耗函数最优解的算法。

初始 置Z＊＝∞，l＝0。

步骤1 当l≤n时：

步骤1.1 通过式（10）计算cij（l）的值；

步骤1.2 解指派问题P2（l），确定工件的最优排序π＊＝［1］，［2］，…，［n］和极小化费用Z（l）；

步骤1.3 如果Z（l）＜Z＊，那么，置Z＊＝Z（l），l＊＝l，π＊（l＊）＝π＊（l）；

步骤1.4l＝l＋1。

步骤2 当l＝l＊，π＊（l）＝π＊（l＊）时，通过引理5计算最优资源分配u＊（l），通过式（3）计算最优加工时间

定理2 算法3在O（n4）时间内解决了在CON型工期分派方法下，这个问题的目标函数为一个凸资源消耗函数时的最优解。

4 结 语

现实生活中，学习效应是普遍存在的，本文将学习效应与可控加工时间相结合，使得问题更具有广泛应用性和实际意义。这个问题在多机环境下或者加工时间为其他资源消耗函数的情形有待进一步研究。

［1］LEYVAND Y，SHABTAY D，STEINER G A.A unified approach for scheduling with conwex resource consumption functions using positional penalties［J］.Eur J Oper Res，2010，206（2）：301－312.

［2］SU L H，LIEN C Y.Scheduling parallel machines with resource dependent processing times［J］.Int J Prod Econ，2009，117（2）：256－266.

［3］SHABTAY D，STEINER G.A bicriteria approach to minimize the total weighted number of tardy jobs with convex controllable processing times and assignable due dates［J］.J Sched，2011，14（5）：455－469.

［4］SHABTAY D，STEINER G.A survey of scheduling with controllable processing times［J］.Disc Appl Math，2007，155（13）：1643－1666.

［5］PANWALKAR S S，SMITH M L，SEIDMANN A.Common due date assignment to minimize total penalty for the one machine scheduling problem［J］.Oper Res，1982，30（2）：391－399.

［6］CHENG T C E，OGAZ C，QI X D.Due－date assignment and single scheduling with compressible processing times［J］.Int J Prod Econ，1996，43（1）：29－35.

［7］SHABTAY D，STEINER G.Optimal due date assignment and resource allocation to minimize the weighted number of tardy jobs on a single machine［J］.Manuf Serv Oper Manage，2007，9（3）：332－350.

［8］BISKUP D.Single－machine scheduling with learning considerations［J］.Eur J Oper Res，1999，115（1）：173－178.

［9］BISKUP D.A state－of－the－art review on scheduling with learning effect［J］.Eur J Oper Res，2008，188（2）：315－329.

［10］WANG D，WANG M Z，WANG Jibo.Single－machine scheduling with learning effect and resource－dependent processing times［J］.Comput indust Eng，2010，59（3）：458－462.

［11］MOSHEIOV G，SIDNE J B.Scheduling with general job－dependent learning curves［J］.Eur J Oper Res，2003，147（3）：665－670.

［12］KAHLBACHER H G，CHENG T C E.Parallel machine scheduling to minimize costs for earliness and number of tardy jobs［J］.Disc Appl Math，1993，47（2）：139－164.