固态自旋在自旋热库与光场作用下的动力学演化

蒋峰建，胡新广，黄志勇

(黄山学院 机电与信息工程学院，安徽 黄山245041)

固态自旋——微腔耦合体系被用于构建基于混合系统的量子计算机。[1]鉴于当前尚未找到能够建造大规模量子计算机的单一物理体系，人们最近提出了将不同物理体系联合起来，取长补短, 搭建基于混合体系的高性能量子计算机。目前最受关注的是固态自旋与超导线路相结合的方案，该方案采用典型的量子图灵机架构：拥有很长相干时间的固态自旋被用作存储器来存储量子信息，与外界有较强耦合的超导量子比特被作为处理器来进行快速的逻辑门操作，在它们之间传递数据的”总线”则通过易于集成的超导传输线腔来实现。因此，固态自旋——微腔耦合体系是这个设计中的关键环节。对于固态自旋——微腔耦合体系的理论研究，目前正在逐渐展开。这个体系由于混合了固态自旋系统和微腔中的光场，同时固态自旋系统周围又存在自旋热库，因此整个体系的动力学演化过程比较复杂。在理论上，人们首先需要了解固态自旋体系、自旋热库和腔场的动力学演化过程，理清这些不同的相互作用对于固态自旋体系的影响。

1 物理模型

假设一个二能级系统S、腔场F与自旋热库B构成了一个封闭体系，其哈密顿量写为:[2]

其中，w0是系统的塞曼分裂能级；

wf是腔场中单模光场的频率；

g是光场与系统自旋的耦合强度；

最后一项中的Jk是系统自旋与第k个核自旋之间的耦合强度。

在外界的强磁场作用下，系统和热库自旋都会有能级分裂，由于自旋热库是核自旋，系统对应于电子自旋，核自旋能级分裂相比于电子自旋的能级分裂项要小的多，因此可以忽略掉核自旋的哈密顿量。上边的哈密顿量中的系统自旋与核自旋的耦合，我们假设为依辛相互作用，而忽略了更复杂的超精细耦合项，这是因为我们假设整个体系处在强磁场下。(1)式转化为相互作用表象后，[3，4]可以写成：

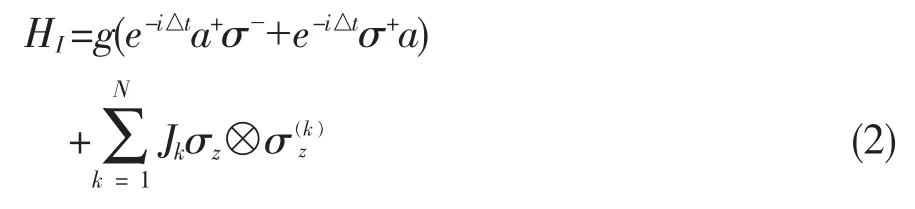
2 系统和光场与自旋热库共同演化

假设有N个自旋热库，其初始态为可分离的纯态│+〉⊗N，在计算基的表示下│+〉表示为:│+〉=(│0〉。二能级系统与自旋热库、以及光场共同组成的初态可以写为:

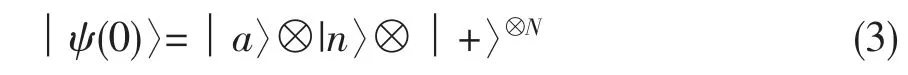
由于系统和自旋热库之间相互作用哈密顿量是依辛耦合，[5]使得自旋热库的状态不会出现量子比特翻转，始终保持在原有的子空间内演化。对于公式(1)中的哈密顿量，系统与光场之间的相互作用已经进行了旋波近似，不出现双光子过程，光子数守恒。因此任意时刻t所对应的态可以写为一系列的态矢量叠加，即：

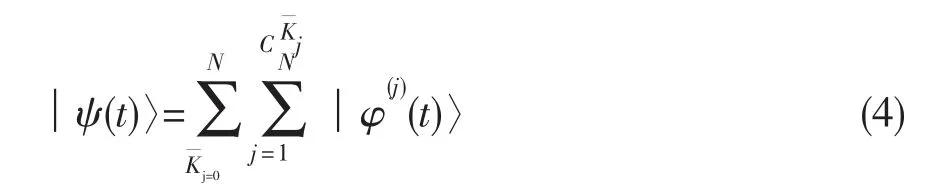
其中

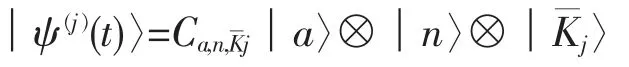
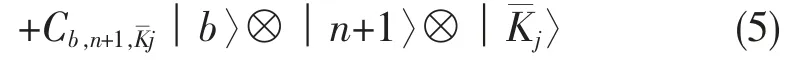
当t=0 时，分量│φ(j)(t)〉对应初态是│φ(j)(0)〉=。在这里，我们把自旋热库态在计算基{│0〉,│1〉}下展开，在N个自旋热库粒子中，当有个处于│1〉态时，我们标记为，这样的态共有种组合，每一种情况的组合用态矢来表示。对于初始的态在哈密顿量作用下只会跃迁到│b〉。在(2)式哈密顿量的作用下，有薛定谔演化方程：

其中令h=1，设系统自旋和每个热库自旋之间的耦合系数近似为相等，令为Jk=J。把任意时刻的总的态矢量(4)式代入(6)式，考虑│ψ(t)〉中任意一个分量│φ(j)(t)〉，其演化过程总是在各个分量│φ(j)(t)〉自身的一个子空间中进行。因此，不失一般性，(6)式右边有:

把(7)式代入(6)式，写成矩阵形式：

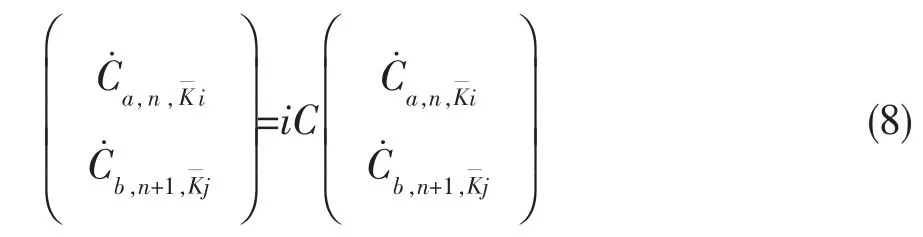
其中

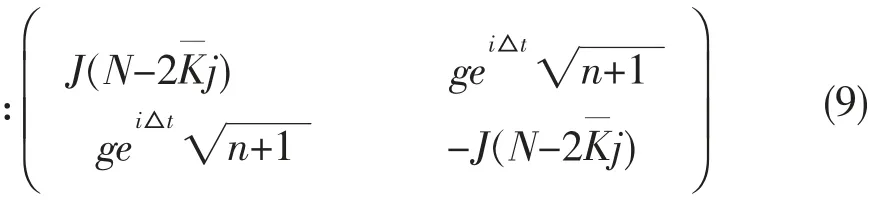
当光场和系统自旋达到共振，有△=0，使得整个哈密顿量不含时，我们可以直接写出幺正演化算子：

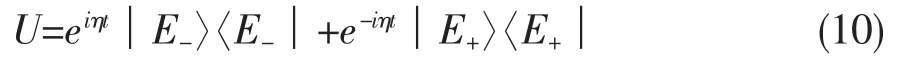
其中

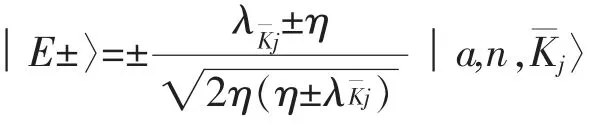
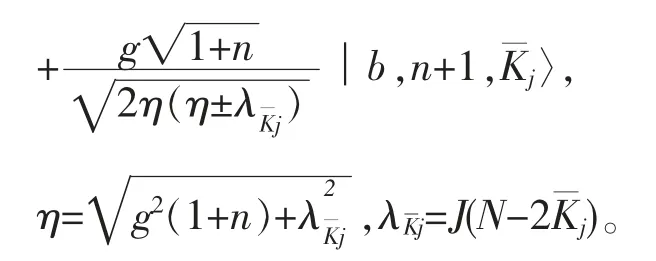
当把幺正演化算子表达式(10)作用到│ψ(0)〉的任意分量初态│φ（j）(0)〉后，得到在任意时刻t的态矢量表达式，写为:

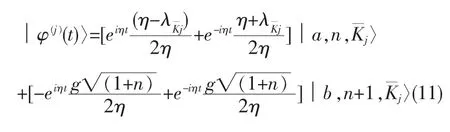
把(11)式代入(4)式，得到系统随时间的动力学演化的约化密度矩阵：

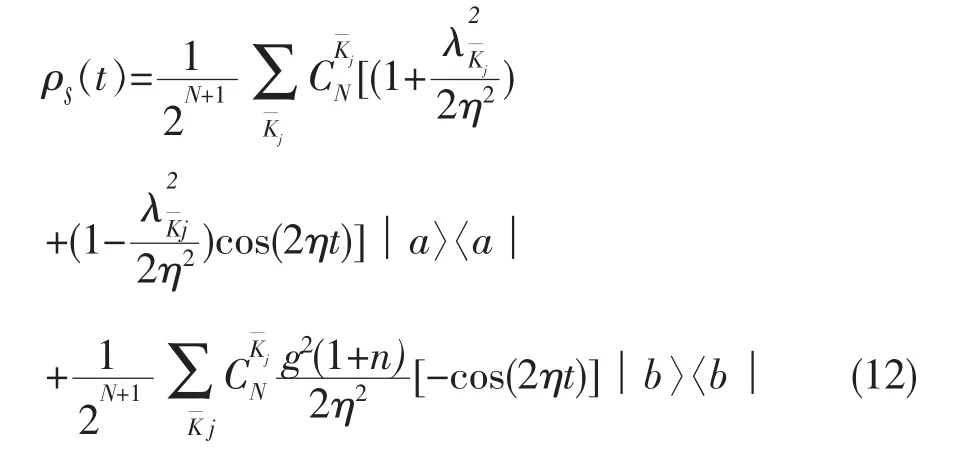
3 总 结

在这里，讨论了固态自旋体系受到自旋热库与光场共同作用下的动力学演化情况。在简化的模型下，我们得到了其密度矩阵随时间演化的解析形式。这个问题的讨论，也许对于理解和认识在固态量子体系中，如何有效操控固态自旋有一定的帮助。

[1]MA Nielsen, I L Chuang.QuantumComputation and QuantumInformation [M].Cambridge: Cambridge University Press, 2000:297-300.

[2]H P Breuer, F.Petruccione.The Theory of Open Quantum Systems [M].Oxford: Oxford University Press, 2002:115-116.

[3]张永德.量子力学[M].北京：科学出版社，2008:300-302.

[4]M O Scully, M S Zubairy.Quantum Optics[M].Cambridge:Cambridge University Press ,1997:194-197.

[5]F M Cucchietti, J P Paz, W H Zurek.Decoherence from spin environments[J].Phys Rev A,2005,72:052113.