全光纤量子通信系统中的高速偏振控制方案*
李申1) 马海强2)3) 吴令安2)† 翟光杰1)
1)(中国科学院空间科学与应用研究中心空间科学实验技术研究室,北京 100190)
2)(中国科学院物理研究所,北京凝聚态物理国家实验室,光物理重点实验室,北京 100190)
3)(北京邮电大学理学院,北京 100876)
1 引言
量子保密通信作为一个新兴的领域是目前国际研究的热点之一,通信双方将一个真随机数比特序列加载在一串单光子上,通过量子信道最终建立相同的密钥,从而实现量子密钥分发.通常的实验系统分为相位编码和偏振编码两种.而无论采用哪种编码方案,准确控制偏振态直接关系着系统的稳定性和误码率.在自由空间的量子保密通信系统中,已有很高速的电光相位调制器可用来实现偏振控制.1992年Bennett等[1]在自由空间的量子保密通信演示系统中,利用泡克耳斯盒实现了光四种偏振态的随机输出.但在较为成熟的全光纤量子密钥分发系统中,通常采用光纤偏振控制器来实现对偏振态的调节与纠正.而传统的光纤偏振控制器件是一种无源器件,通过对光纤的挤压来控制输出光的偏振方向[2,3].这种机械式的控制方法只可用于一般的静态偏振态的调节,通常可用于相位编码的全光纤量子密钥分发系统中,但对于偏振编码的全光纤量子密钥分发系统[4],则需要对光子偏振态进行高速的调制,而这种机械式的无源光纤偏振控制器就很难达到精确与高效的控制.其实,偏振控制的研究几乎是与单模光纤的出现同时开始的,随着光纤通信的迅速发展,偏振控制技术一直在不断地更新.1979年,Johnson[5]首先提出了基于电磁挤压的光纤型偏振控制器.此后相继出现了电光晶体型[6]、法拉第旋转型[7]以及延迟耦合型[8]等各种各样的偏振控制器.1989年Aarts与Khoe[9]研制了一种新型无端偏振控制器,解决了偏振控制的复位问题,为其实用化奠定了基础.2002年Hirabayashi与Amano[10]研制成功了低压液晶偏振控制器.2003年Yoshino等[11]提出了高速全光纤偏振控制器.2011年范飞等[12]提出了多功能磁光子晶体太赫兹可调偏振控制器件.尽管如此,对于偏振编码的量子密钥分发系统,仍旧需要高速精准的偏振控制器来实现高效的信息加载.所以高速、精确、低成本的偏振控制器仍然是偏振控制的主要研究方向.在量子密钥分发实验系统中,为了获得高速的信息加载,通常采用多台光源产生各种偏振光然后再利用偏振分束器将这些不同偏振态的光耦合进同一信道中的方法来替代偏振控制器[1314].此方法虽然解决了偏振控制的精准与高效的问题,但它的最大缺点是实现成本非常大,而且控制系统十分复杂,对控制电路的精确度以及同步性要求十分高.所以,基于相位编码偏振检测的量子密钥分发方案[15],我们提出一种结构简单、成本低的解决光纤中偏振高速控制的方法.此方法不需要多个法拉第镜,并且可以在一个端口直接输出各种偏振态的光,无需再进行后续耦合操作.该方法可以对一束恒定的输入光,通过电调节高效地产生各种不同偏振方向的输出光.由于该方法采用了电控制,工作速度取决于电控装置的工作速度,所以不仅可以工作在高速状态,而且可以精确地控制输出光的偏振方向,避免了机械控制带来的弊端.
2 理论原理
偏振光最一般的形态是椭圆偏振光,线偏振光和圆偏振光都可看作是椭圆偏振光的特例[16].假设光沿z轴传播,那么一般的椭圆偏振光矢量可看作是沿x轴(水平方向)的线偏振光和沿y轴(垂直方向)的线偏振光的合成.
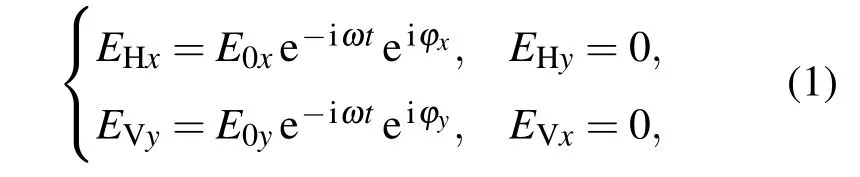
其中,EHx,EHy分别表示水平线偏振光在x,y轴上的投影,EVx,EVy分别表示垂直线偏振光在x,y轴上的投影,E0x,E0y分别表示水平和垂直偏振光的振幅,ω为光的圆频率,φx,φy分别为水平和垂直线偏振光的相位.
略去公因子 e-iωt,则此椭圆偏振光矢量可用列矩阵表示为

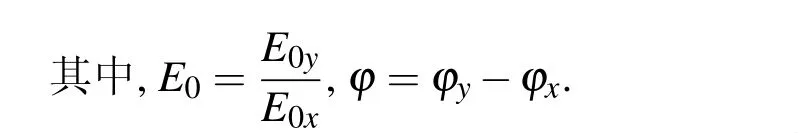
由(3)式可见,只要通过适当地改变相位差φ和振幅比E0就可以获得一系列我们想要得到的偏振光.
在量子密钥分发的众多协议中,Bennett与Brassard在1984年提出的通信协议(简称BB84协议)[17]被认为是最为经典的协议,它的安全性基于量子力学的基本原理,在理论上已被人们证实.其协议的具体操作中需要高速地随机发送和检测属于两组共轭基的偏振光,一组是线偏振的,一组是圆偏振的,共4种偏振态的光子[18].在本文提出的偏振控制方案中,可令振幅比为E0=1,相位调制器分别加载0,π/2,π和3π/2这四种相位所对应的电压,即可以分别产生45◦线偏振光,右旋圆偏振光,135◦线偏振光和左旋圆偏振光.
3 实验装置
实验光路如图1所示.
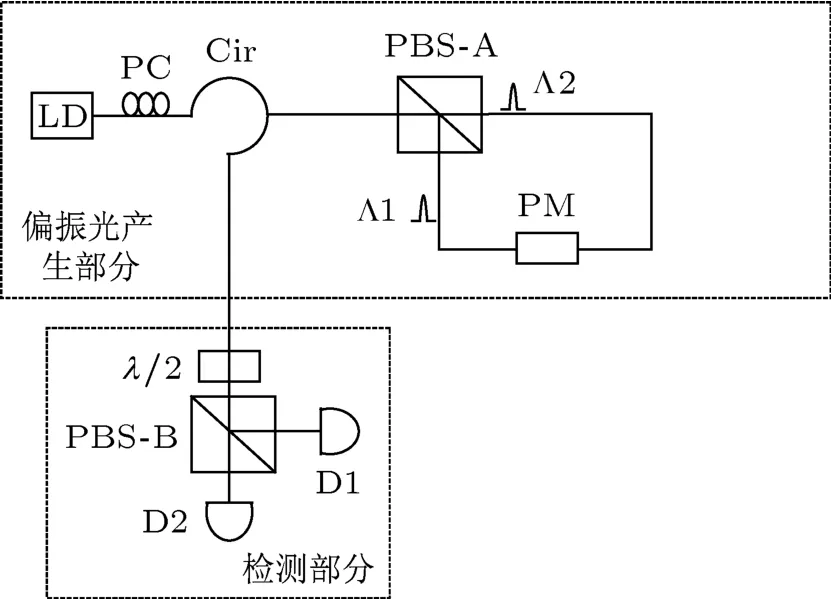
图1 偏振控制方案实验光路图,LD,脉冲激光器;PC,偏振控制器;Cir,环形器;PBS-A,PBS-B,偏振分束器;PM,相位调制器;λ/2,半波片;D1,D2,光功率计
3.1 偏振光的产生
在实验系统中,由脉冲激光器(advanced laser diode systems,PIL131DFB-SM)产生一恒定偏振态的激光脉冲,其波长为1310 nm,脉宽20 ps,重复频率1 MHz.利用传统的光纤线圈式结构偏振控制器PC将激光脉冲转为45◦的偏振方向,光通过环形器Cir以后,由偏振分束器PBS-A分成两束强度相等的偏振方向正交的激光脉冲Λ1和Λ2.为方便起见,定义前者为垂直偏振方向,后者为平行偏振方向.这两束光经过传播方向相反但距离相等的光程后,在PBS-A处叠加,形成一个双向Sagnac环.在这个过程中,相位调制器PM会对垂直偏振方向的激光脉冲Λ1进行相位调制.所采用的电光相位调制器为重庆中国电子科技集团公司第四十四研究所生产,工作于单线偏振状态,器件的输入、输出口均用保偏光纤.我们自制的相位驱动电路,其半波电压约为4.2 V,选择0,2.1,4.2,6.3 V电压可分别实现0,π/2,π,3π/2的相位调制,调制频率为1MHz,最高调制速率可达2 GHz,精度为10-3rad.由(3)式可知,在PBS-A处两束光叠加后的结果取决于两束光的相位差,即PM的调制相位.叠加产生的光脉冲经过环形器Cir输出.
3.2 生成偏振光的检测
产生的偏振光用半波片、偏振分束器PBS-B和光功率计D1和D2进行测量.半波片的作用是将光的偏振方向旋转45◦.如表1所示,不同相位差产生的不同方向的偏振光,经过半波片后,偏振方向的变化导致通过偏振分束器PBS-B后,在光功率计测量的结果不同.光功率计D1和D2两行表示所测得的光强的百分比.
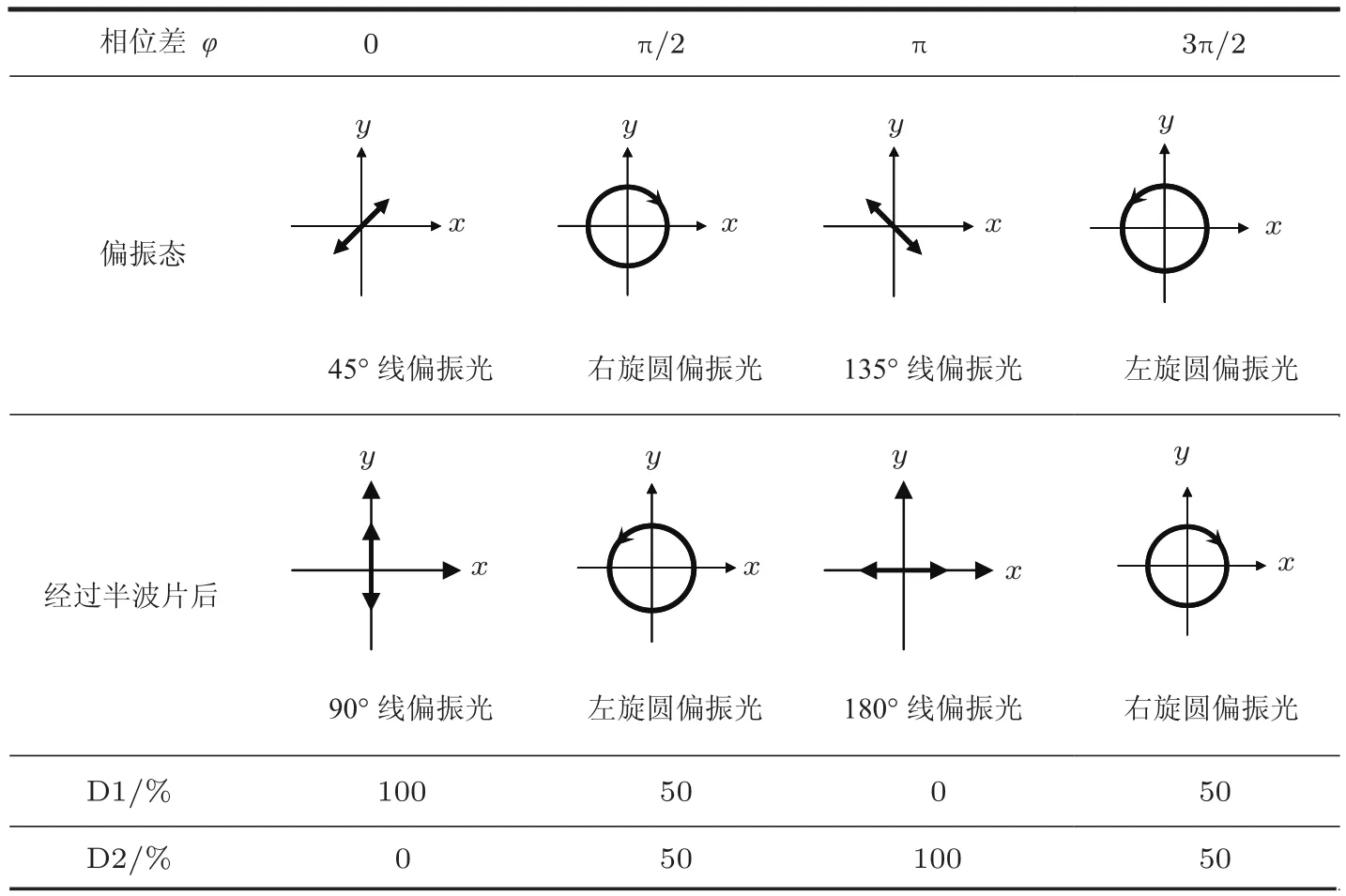
表1 不同偏振光的测量结果
从表1可以看出系统产生的不同线偏振态的光可以通过D1和D2的计数不同反映出来.
4 实验结果
生成偏振光的检测结果如图2所示.从图2中可以看出,在不同的调制电压下对应于不同的偏振光的输出.当相位调制器加载4.2 V的电压时,会有135◦的线偏振光从Sagnac环输出.到了检测系统的半波片后偏振态会旋转45◦,变为水平的线偏振光,最后将全部透过偏振分束器由D2探测,D1将不会探测到任何光的输出.从图中可以看出,当D1输出的光功率为0,D2输出的光功率最大时,对应的相位调制器的调制电压值恰好是4.2 V,理论与实验符合得非常好.但由于检偏光路中两个光功率计D1,D2的探测效率不同以及偏振分束器PBS-B的两个输出端口与光功率计的耦合效率的差异,导致图中D1光功率的最大值与D2光功率的最大值不同.图2中D2探测到的最大值为15.00 nW,而此时D1的读数为0,即光强已小于功率计的探测灵敏度.若按功率计灵敏度为0.01 nW估算,则消光比为-10×lg(0.01/15)=31.76 dB.但实验中所用的偏振分束器PBS-A的消光比为30 dB,它决定了系统所产生偏振光的最大消光比.根据分析,实验误差是系统中各器件以及光纤对光的衰减和探测器的误差所引起的.综合考虑,此系统生成偏振光的最大消光比可达30 dB.
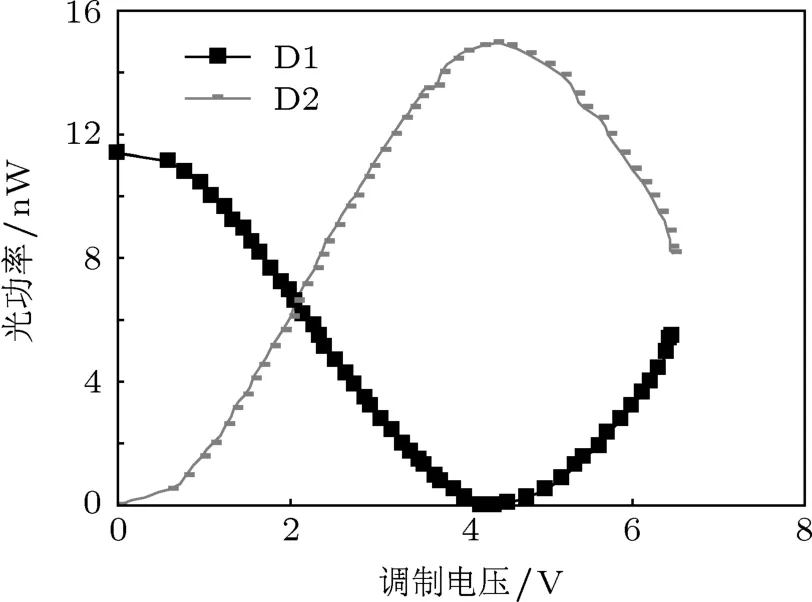
图2 生成偏振光的检测结果
将此偏振控制方案应用于基于BB84协议的偏振编码的量子密钥分发系统中时,只需要将相位差分别调制到0,π/2,π和3π/2,即可以分别产生45◦线偏振光、右旋圆偏振光、135◦线偏振光和左旋圆偏振光.此方案的偏振控制速率完全取决于相位调制器的工作频率.目前,市场上商用的相位调制器的工作频率可达40 GHz,所以此方案最快的偏振控制速率可达到40 GHz.本文中的实验只是进行一个原理性的验证.由于受限于实验室所使用的相位调制器的工作频率,本文的方案演示只可达到2GHz,但这已能完全满足目前基于偏振编码的量子密钥分发系统中所需的偏振控制速率.
5 结论
本文提出的全光纤的偏振控制方法,采用的是Sagnac环中加电光相位调制的工作方式,通过不同的相位调制而精确输出各种偏振光,并且实现了单个端口直接输出各种偏振态的光,无需后续耦合操作.其光路简单,易于调节,所需器件少,系统稳定性极高.由于本方案是通过电控相位调制器的方法来实现不同的偏振光的输出,所以系统可以工作在很高的频率下,无论从偏振控制的精准度上还是控制速率上均可满足量子通信系统的要求.此外,由于采用全光纤的光路系统,将来可通过集成光学技术实现微小尺寸的封装,成本低廉.
[1]Bennett C H,Bessette F,Brassard G,Salvail L,Smolin J 1992 J.Cryptology 5 3
[2]Li H W,Wang S,Huang J Z,Chen W,Yin Z Q,Li F Y,Zhou Z,Liu D,Zhang Y,Guo G C,Bao W S,Han Z F 2011 Phys.Rev.A 84 062308
[3]Zhao H,Ma H Q,Li Y L,Wu L A 2005 Acta Sin.Quantum Opt.11 2(in Chinese)[赵环,马海强,李亚玲,吴令安2005量子光学学报11 2]
[4]Gordon K J,Fernandez V,Townsend P D,Buller G S 2004 IEEE J.Quantum Electron.40 900
[5]Johnson M 1979 Appl.Opt.18 1288
[6]Kidoh Y,Suematsu Y,Furuya K 1981 IEEE J.Quantum Electron.17 991
[7]Okoshi T,Cheng Y H,Kikuchi K 1985 Electron.Lett.21 787
[8]Liu D M,Huang D X,Nie G 1993 Acta Opt.Sin.13 1120(in Chinese)[刘德明,黄德修,聂刚1993光学学报13 1120]
[9]Aarts W H J,Khoe G D 1989 J.Lightwave Technol.7 1033
[10]Hirabayashi K,Amano C 2002 IEEE Photion.Technol.Lett.14 504
[11]Yoshino T,Yokota M,Kenmochi T 2003 Electron.Lett.39 1800
[12]Fan F,Guo Z,Bai J J,Wang X H,Chang S J 2011 Acta Phys.Sin.60 084219(in Chinese)[范飞,郭展,白晋军,王湘晖,常胜江2011物理学报60 084219]
[13]Liu Y,Chen T Y,Wang J,Cai W Q,Wan X,Chen L K,Wang J H,Liu S B,Liang H,Yang L,Peng C Z,Chen K,Chen Z B,Pan J W 2010 Opt.Express 18 8587
[14]Shao J,Wu L A 1995 Acta Sin.Quantum Opt.1 41(in Chinese)[邵进,吴令安1995量子光学学报1 41]
[15]Ma H Q,Zhao J L,Wu L A 2007 Opt.Lett.32 698
[16]Yao Q J 2002 Optical Tutorial(Beijing:Higher Education Press)p362(in Chinese)[姚启钧2002光学教程(北京:高等教育出版社)第362页]
[17]Bennett C H,Brassard G 1984 Proc.IEEE Internat.Conf.on Computers Bangalore,India,December 10-19 1984,p175
[18]Wu L A 1998 Physics 27 544(in Chinese)[吴令安1998物理27 544]

