光弹在库墨-高斯晶格中传输特性的研究*
周博臻 徐四六 程正则
(湖北科技学院电子与信息工程学院,咸宁 437100)
1 引言
20世纪80年代以来,光束在非线性介质中传播时,如果非线性效应恰好能和衍射效应相平衡,光束在传播过程中保持形状不变,此光束就称为光学空间孤子.目前,光学空间孤子的研究正从简单结构到复杂结构孤子,从标量到矢量孤子,从相干到非相干孤子,从均匀介质到离散系统中的晶格孤子,以及从局域非线性到非局域非线性孤子发展.稳定性是孤子研究的一个重要方面,因为从物理上考虑,只有稳定的孤子才能在实验中观察和控制.而光弹,或者说时空光孤子,在非线性光学介质中是真实存在的,是当非线性调制使衍射和散射同时达到平衡时形成的稳定波包[1-6]考虑高维(二、三维)的情况时,光弹在克尔介质中通常是不稳定的,因此得到稳定性的光弹显得十分重要.令人欣慰的是,到目前为止有许多可以使光弹更加稳定的设计方案已经被报道.如稳定的光弹既可以在饱和或完全非线性介质[7-9]、二次型的[10,11]或非局域非线性介质[12-14]、非线性介质进行串联的光学几何体[15,16]等中形成,也可以存在于不同光波导阵列和光学晶格的材料中[17-22].
特别地,由于光学晶格具有空间周期性的特点,其对光波具有很好的囚禁作用,能够使光波在非线性介质中形成稳定的光孤子.研究光弹在光学晶格中的形成和传输时,其非线性的介质通常假设为均匀的.然而,目前的技术已经允许介质具有线性和非线性折射率分布的性质,这种可能已经在玻色-爱因斯坦凝聚中有关孤子的研究中得到了充分的体现.例如,玻色-爱因斯坦凝聚可形成于这样的光学晶格中,这种晶格原子间的相互作用的空间调制可以通过使用施加了非均匀的外加磁场或光学场的费希巴赫(Feshbach)共振态获得[23];同样,在工程上,线性和非线性折射率也可能存在于周期性的光学结构中等等.
本文首先建立一个在库墨-高斯周期性光学晶格中光弹传输的理论模型,接着通过数值模拟和计算对理论模型进行研究.结果表明,在这种周期性的光学晶格中,在一定的参数范围内光弹的传输是稳定的.
2 理论模型
研究在异相调制的二维库墨-高斯光学晶格中的三维光弹的传输特性.假定光束在含有异相线性与非线性晶格的介质中沿着z轴传播,描述光弹的传播方程是非线性薛定谔方程,其无量纲复合场振幅为q,归一化后的方程为

其中R(r)是库墨-高斯函数调制的晶格,r=(x2+y2)1/2,σ是非线性调制深度,p为线性调制深度.R(r)=(-n,m+1,r2)(m=0,1,2,···) 为库墨-高斯晶格系数,F′(-n,m+为连带库墨多项式.注意到当非线性系数1-σR(r)在某个状态达到极小值(极大值),线性系数pR(r)达到极大值(极小值),这种状态称为异相调制.研究发现对于库墨-高斯晶格,无论σ为何值时,1-σR(r)和pR(r)为反相,因此调制变成了反相.方程(1)的整个守恒的能量U,哈密顿量H为

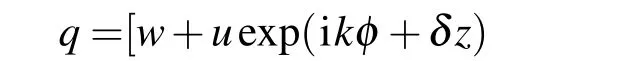
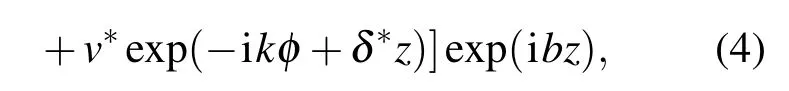
其中u,v是基态解的微小扰动.将(4)式代入方程(1)中,得线性u,v的本征值方程:
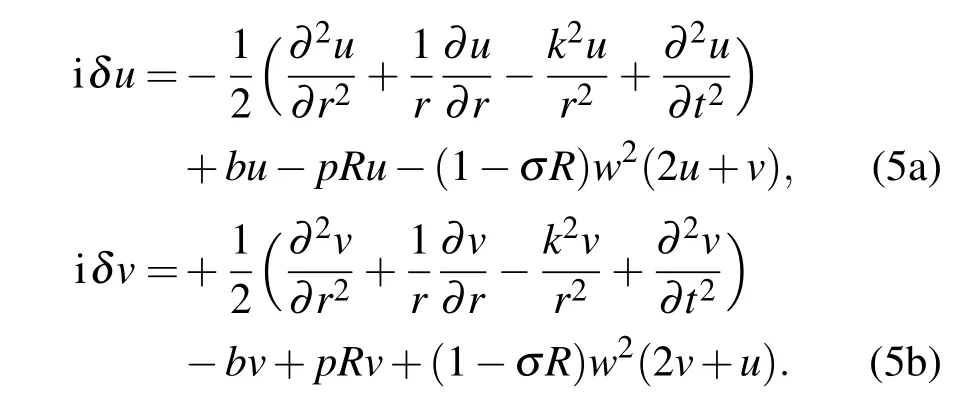
通过对方程式(5a)和(5b)的数值求解,以判别时空孤子的稳定性.
3 数值计算与分析
当晶格为线性晶格时(即σ=0),若非线性强度较低,采用快速虚时间演化法(AITEM)[25]对方程(1)进行数值求解.由图1(a)和(b)可知,当传播系数b逐渐增加到接近于bco时,孤子恰好实现由不稳定到稳定的转换,其场的空间分布或时间分布可以延展到全部空间或时间.时空孤子空间场分布覆盖了库墨晶格环.当孤子的强度增加时,此时光弹在r的方向上没有改变,其时间分布有明显的改变,当r=0,τ=0时,其极小值变成极大值,并且在-2<τ<+2范围内出现了三个极大值和两个极小值.因此当线性和非线性晶格的影响较强时,光弹的场分布的形状和大小随着传播系数的改变而改变.

图1 (a),(d)τ=0时库墨晶格中的空间场分布;(b),(e)r=0时的时间场分布;(c),(f)采用AITEM法求解方程(1)得到稳定孤子解所需迭代的次数,传播常数分别为(a),(b)b=2.25,(c),(d)b=2.37,p=0.4,σ=0.2
不同于文献[26],在二维Bessel反向调制的晶格中,孤子波幅的增长会使光弹在空间的分布有较大的改变,当非线性对晶格折射率的影响大于线性对折射率的影响,使光进入非线性较强的区域.本文中的晶格采用库墨-高斯晶格,研究表明,当传播常数b处在较小值时,时间上的扰动对波形有较大的影响,使孤子分布出现震荡,但是仍然能保持稳定,而在空间上波形仍能保持稳定(图1(a)和(b)).当传播常数b处在较大值时,尽管时间上的扰动对波形仍然有所影响,但相对于较小的b,这个波形较为集中;而在空间场中,波形没有变化,但幅值变大了(图1(d)和(e)).用AITME迭代法计算孤子的稳定解,发现当传播常数为2.25和2.37,迭代次数分别为900和460时,可以得到稳定的孤子解图1(c)和(f).
图2(a)为能量随着传播系数的变化关系.由图中可知,当非线性系数一定时,基态孤子的能量随着传播系数的增加而增加;U(b)曲线的斜率是正的(即dU/db>0),并且随着非线性系数σ的增大,能量增加的越快.图2(b)为哈密顿量与光弹的能量的对应关系.可以看到,哈密顿量随着光弹的能量增加而增加,当能量在0<U<3范围内,非线性晶格系数对哈密顿量的影响较小,当U>3时,非线性系数越大,哈密顿量增加的越快.进一步研究表明(图2(c)和(d)),k为方位角扰动指数,其反映了方位角大小,从而影响时空孤子的角动量.当k=0时,非线性晶格常数σ=0.8,在0<b<12与b>15范围内,光弹是稳定的,只有在12≤b≤15范围内光弹才会受到微扰的影响.而当方位扰动指数k=1时,光弹受微扰影响的范围没有变化,只是相较于k=0时前移到了10≤b≤13.当非线性晶格常数改变由0.8变为1.2时,光弹受微扰影响的区间与σ=1.2相比没有显著的改变,只是b的区间减少为8.5≤b≤11.5(k=0)和7.5≤b≤10.5(k=1).由此可见,非线性晶格系数显著地调制了光弹的传播特征和能量.
Bessel晶格中光弹传输特性的研究表明[26],在σ=0时,仅当微扰的系数k=0才会使光弹的解出现扰动;但对于库墨-高斯晶格,在非线性调制下的库墨晶格,当k=1时,光弹也会出现扰动,这主要是因为高振幅的时空孤子在空间中传输时形成环状结构.此时,当非线性调制深度超过某个值时,方位角将变得十分不稳定,而这个临界值为σcr,其与晶格的线性调制深度p是相关的(例如,当p=12时,σcr≈ 0.65).

图2 (a)传播常数与能量关系;(b)能量与哈密顿量的关系,其中参数p=12,σ=0,1.5,2.7;(c),(d)传播常数b与微扰因子实部的关系,其中参数p=12,(c)σ=0.8,(d)σ=1.2
为了进一步研究光弹的传输特性,采用分布傅里叶算法对方程(1)进行数值仿真,入射光为高斯光,其初始值为q0=0.1e-(x2+y2+t2).由图3(a)-(c)可知,库墨晶格强度分布具有空间周期性,其明显的调制时空孤子的时空分布和相位特性;由图3(d)-(f)和图4可知,当m=3或m=2时,光弹可以形成一种奇异的时空孤子簇,其光强在x-y平面内由6个或4个同心的圆柱形的峰组成,每个圆柱包中间存在着一定程度的凹陷,并且随着传播距离的增加,其强度不断减小.由图3(h)-(j)可知,孤子的相位分布决定于方位数m,其特性被空间所调制.

图3 (a),(b),(c)为周期性晶格的分布,其中m值分别为2,3,4;(d),(e),(f)为光弹在不同传播距离z=40,60,100时光强在x-y平面内的分布;(h),(i),(j)为与(d),(e),(f)对应的相位分布,此时参数m=2,p=10,σ=0.9
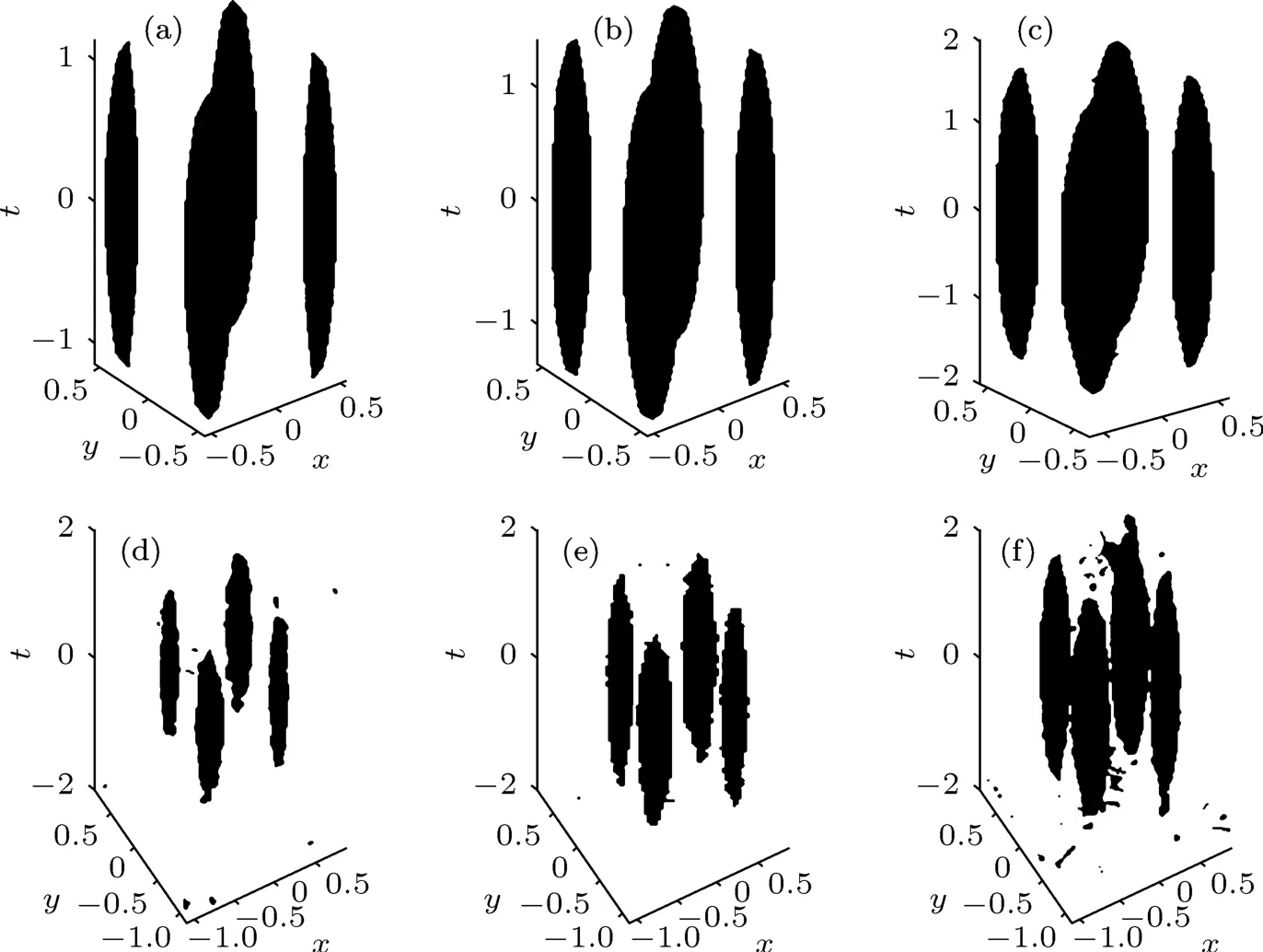
图4 (a),(b),(c)光弹在不同传播距离z=40,60,100时的等值图;(d),(e),(f)是加入微扰Ω=0.8后的等值面图;相关参数p=0.2,σ=1,m=2
由图4可以看出,当m=2时,光弹由4个时空孤子组成,随着传播距离的增加,等值面图中4个孤子的距离逐渐减小.为了进一步验证时空孤子解的稳定性,在仿真时加入白噪声Ω=0.8,并且传输距离取到z=100,发现加入白噪声后孤子的等值面图没有受到显著地影响,因此光弹的传输是稳定的.
图5和图6分别为不同传输距离时光弹的等值面分布图.由图可知,光弹的时空分布决定于方位角m,光弹可以分为不同数目的孤子组成一类同心的时空孤子簇,这些不同数目的孤子围成一个同心的圆环,每个孤子具有纺锤形的分布,孤子的数目为2m,且随着传播距离的增加孤子间的间距逐渐减小.同时发现光弹的相位分布决定于方位角,体现对称的径向分布.

图5 (a),(b),(c)为m=3,传播距离分别为z=40,60,100时,输出光的等值面图;(d),(e),(f)是(a),(b),(c)所对应的相位图,参数 p=0.2,σ=1
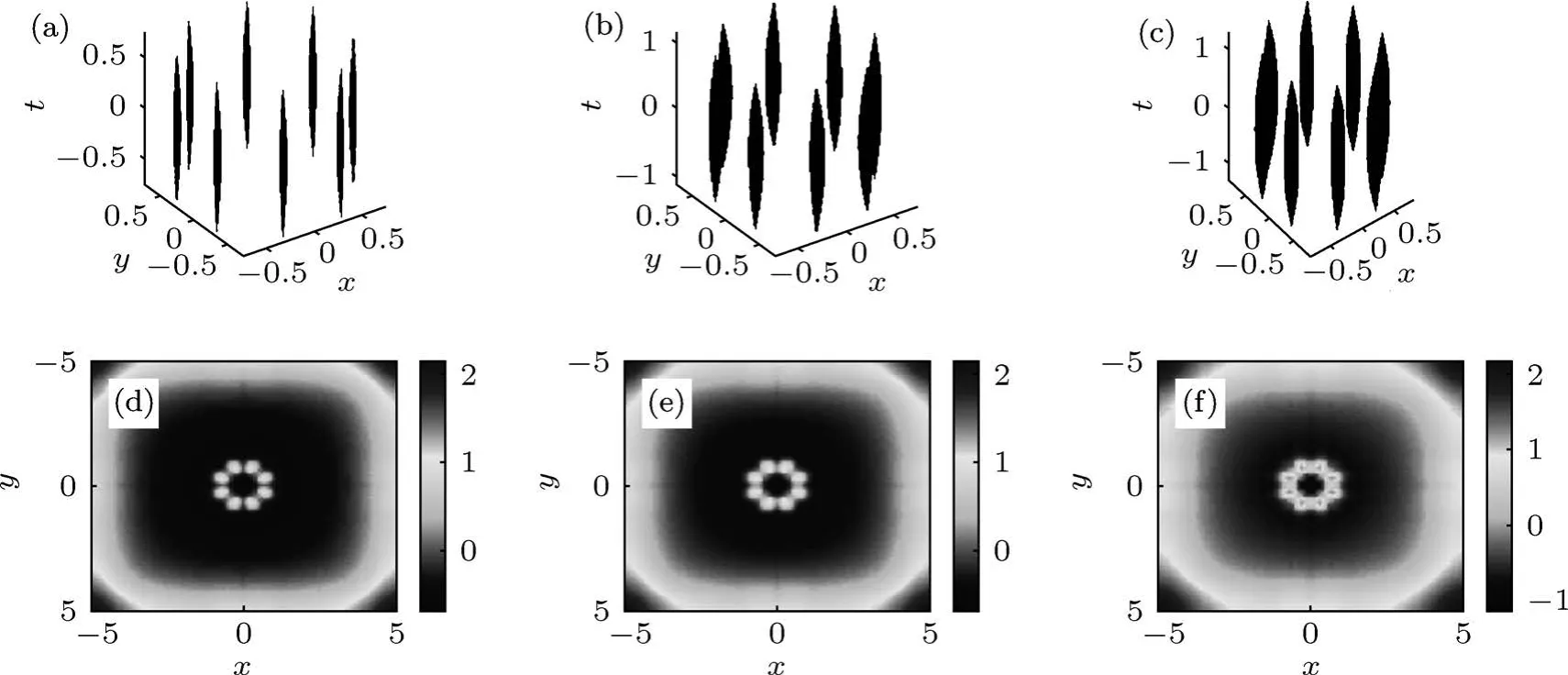
图6 (a),(b),(c)为m=4,传播距离分别为z=40,60,100时,输出光的等值面图;(d),(e),(f)是(a),(b),(c)所对应的相位图,参数 p=0.2,σ=1
4 结论
本文研究了光弹在线性和非线性异相调制的库墨-高斯晶格中传输的特性;发现线性和非线性库墨-高斯晶格能显著地改变光弹的形状及其稳定范围,晶格的非线性调制深度可以很好地控制稳定性区域的宽度;特别地,稳定时空光孤子的能量会随着非线性调制深度的加强而增长.
[1]Silberberg Y 1990 Opt.Lett.15 1282
[2]Malomed B A,Mihalache D,Wise F,Torner L 2005 J.Opt.B 7 53R
[3]Xu S L,Beli´c M R,Zhang W P 2012 J.Opt.Soc.Am.B 29 1
[4]Wu Z,Wang Q,Wei Q 2001 Acta Phys.Sin.50 489(in Chinese)[吴中,王奇,卫青2001物理学报50 48]
[5]He G G,Wang X S,She W L 2002 Acta Phys.Sin.51 2270(in Chinese)[何国岗,王晓生,佘卫龙2002物理学报51 2270]
[6]Liu J S,Hao Z H 2002 Acta Phys.Sin.51 2772(in Chinese)[刘劲松,郝中华2002物理学报51 2772]
[7]Edmundson D E,Enns R H 1992 Opt.Lett.17 586
[8]Desyatnikov A,Maimistov A,Malomed B 2000 Phys.Rev.E 61 3107
[9]Mihalache D,Mazilu D,Crasovan L C,Towers I,Buryak A V,Malomed B A,Torner L,Torres J P,Lederer F 2002 Phys.Rev.Lett.88 073902
[10]TrapaniPD,CaironiD,ValiulisG,DubietisA,DanieliusR,Piskarskas A 1998 Phys.Rev.Lett.81 570
[11]Liu X,Qian L J,Wise F W 1999 Phys.Rev.Lett.82 4361
[12]Bang O,Krolikowski W,Wyller J,Rasmussen J J 2002 Phys.Rev.E 66 046619
[13]Mihalache D,Mazilu D,Lederer F,Malomed B A,Kartashov Y V,Crasovan L C,Torner L 2006 Phys.Rev.E 73 025601(R)
[14]Xu S L,Liu H P,Yi L 2010 Acta Phys.Sin.59 1069(in Chinese)[徐四六,刘会平,易林2010物理学报59 1069]
[15]Torner L,Carrasco S,Torres J P,Crasovan L C,Mihalache D 2001 Opt.Commun.199 277
[16]Torner L,Kartashov Y V 2009 Opt.Lett.34 1129
[17]Aceves A B,Angelis C D 1993 Opt.Lett.18 110
[18]Aceves A B,Angelis C D,Rubenchik A M,Turitsyn S K 1994 Opt.Lett.19 329
[19]Aceves A B,Luther G G,Angelis C D,Rubenchik A M,Turitsyn S K,1995 Phys.Rev.Lett.75 73
[20]BaizakovBB,MalomedBA,SalernoM2004Phys.Rev.A70053613
[21]Mihalache D,Mazilu D,Lederer F,Kartashov Y V,Crasovan L C,Torner L 2004 Phys.Rev.E 70 055603
[22]Mihalache D,Mazilu D,Lederer F,Malomed B A,Kartashov Y V,Crasovan L C,Torner L 2005 Phys.Rev.Lett.95 023902
[23]Lina T C,Weic J,Yao W 2010 J.Diff.Equ.9 2111
[24]Kartashov Y V,Egorov A A,Vysloukh V A,Torner L 2006 Opt.Express 14 4049
[25]Yang J K,Lakoba T I 2008 Stud.Appl.Math.3 265
[26]Ye F W,Kartashov Y V,Hu B B,Torner L 2009 Opt.Express 14 11328

