氧、硫掺杂六方氮化硼单层的第一性原理计算*

张召富 周铁戈 左旭

(南开大学信息学院,天津 300071)

1 引言

六方氮化硼单层(h-BN)[1,2]、氮化硼纳米管(BNNTs)[3,4]、石墨烯[5,6]、碳纳米管[7](CNTs)等都是低维纳米材料,因其独特的结构和优良的力学、热学和光学性能,在自旋电子学[8]、纳米电子学等领域有重要的研究和应用价值.不同于石墨烯和碳纳米管,h-BN单层和BN纳米管在室温下为半导体或绝缘体,具有高温抗氧化等独特性质.这使得他们在某些应用领域优于石墨烯和碳纳米管.通过吸附或者掺杂其他原子,可以改变BN单层的几何结构、磁性性质和电子自旋等物理特性,进一步扩宽其应用领域[9].

作为新型材料,掺杂低维体系和III-V族化合物近年来广受关注[10-13].在III-V族化合物中,BN更加受到青睐,BN单层的性质及原子取代的理论研究与试验验证近年来受到了广泛关注.1995年,Nagashima等[14]研究了h-BN吸附于金属表面是电子结构;2006年,贾建峰和武海顺[15]采用第一性原理计算研究了BN纳米管内含有C纳米管的结构与电学性质;2006年,Ooi等[16]研究了六方BN的电子结构;2007年,Azevedo等[17]采用数值原子轨道展开价电子波函数研究了h-BN中N原子空位,B原子空位,C原子取代N和C原子取代B等情况,给出了不同缺陷的稳定性和形成能等结果;2009年,Azevedo等[18]在前人的基础上又给出了电子结构和磁性性质等结果,解释了有缺陷的BN单层的表面态的形成原因,并且指出能隙和功函数与不同缺陷的电子结构直接相关.除此之外,Si和Xue[19]重点对具有B缺陷和N缺陷的BN单层的磁性进行了研究,给出了态密度和磁矩等结果.

本文采用密度泛函理论(DFT)[20,21],研究了氮化硼单层中氮原子缺陷(VN)、氧原子取代氮原子(ON)和硫原子取代氮原子(SN)等超胞体系的几何结构、磁性性质、电子结构.特别是,利用杂质原子的局域对称性,结合分子轨道理论,解释了杂质能级和磁性的产生.

2 理论模型与计算方法

VASP(vienna ab-initio simulation package)[22]是基于密度泛函理论的第一性原理计算软件包,其可靠性已经得到了大量研究的验证[23-26].本文采用VASP对掺杂体系的晶格结构、磁性性质、电子结构进行计算.采用平面波展开价电子波函数,采用投影缀加平面波(PAW)[27]方法描述离子实与价电子的相互作用.计算中各原子的价电子组态分别为B 2s22p1,N 2s22p3,O 2s22p4,S 3s23p4.采用Perdew,Burke和Ernzerhof(PBE)[28]的广义梯度近似(GGA)描述电子之间的交换关联.经过收敛测试,平面波截断动能设定为400 eV.

计算氧元素和硫元素掺杂的同时,为了进行对比,计算了未掺杂BN单层和具有N缺陷时的情况.计算分为两部分,首先进行几何结构优化,得到稳定的结构,然后对优化后体系的磁性性质和电子结构进行高精度计算.在几何结构的优化中,采用3×3×1的k点网格,当原子受力小于0.02 eV/°A时停止晶格优化,并发现采用5×5×1的k点的优化结果与3×3×1的几乎完全一致.在计算磁性和电子结构时候采用5×5×1的k点网格,能保证总能量收敛到0.01 eV.

h-BN的原胞包含1个N原子和1个B原子.为了实现掺杂并且避免相邻超胞的相互影响,采用7×7的超胞,即由49个N原子和49个B原子组成的包括98个原子的BN超胞;另外用杂质原子(O或S)替换一个N原子.未掺杂的h-BN及掺杂后的六方BN的超胞结构如图1所示,图1(a)是未掺杂的h-BN;图1(b)是具有N缺陷的BN单层;图1(c)和(d)分别是O和S取代BN单层中的N原子后的结构示意图;图1(e)和(f)是对应的侧视图,可以直观反映出掺杂后BN单层的形变.

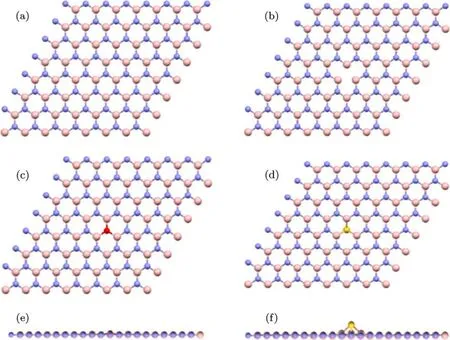
图1 体系的几何结构 (a)未掺杂;(b)N缺陷;(c)O掺杂顶视图;(d)S掺杂顶视图;(e)O掺杂侧视图;(f)S掺杂侧视图

3 计算结果与讨论

3.1 晶体结构和成键能

经过VASP优化之后的BN单层的B-N键键长为1.443°A,与其他理论计算以及实验值1.45°A[29]相一致.O和S掺杂BN单层在优化之后的相关晶格参数和成键能如表1所示.

表1中hB是与掺杂原子最近邻的B原子距BN平面的距离,反映了掺杂后BN单层的形变程度,dOB为掺杂原子与最近邻的B原子的键长,Eb是成键能.成键能的计算方法为:Eb=+EO-Etotal.其中,表示具有N缺陷的BN单层的总能量,EO表示独立的杂质原子的总能量,Etotal表示优化后的体系的总能量.

表1 O,S掺杂BN单层晶格参数和成键能

从图1(e)和(f)以及表1数据可以看出,S掺杂的BN单层的几何形变较大,O掺杂的BN单层几乎没有形变.这是由于S的原子半径比N的原子半径大,掺杂后晶格畸变比较明显,而O和N的原子半径相近,O取代N之后对体系结构影响极小.由于氧的电负性比硫的强,且半径与氮的更接近,所以掺杂后的BN单层形变小且成键能大.

3.2 磁性性质

3.2.1 体系的磁矩

表2给出了氧原子、硫原子掺杂BN单层超胞的总磁矩(M)以及杂质原子(MO)、与杂质原子最近邻的B原子(MB)、次近邻的N原子(MN)、再次近邻的B原子(MB′)的局域磁矩.为了进行对比,同时给出了具有N缺陷的情况.

可以看出,具有N缺陷、O掺杂、S掺杂的BN单层总磁矩均为1µB,其中µB为玻尔磁矩.未掺杂的BN中,B原子和N原子的价电子均成键,无磁矩.当用O或S取代时,由于N原子有5个价电子而杂质原子具有6个价电子,掺杂之后的体系中有一个电子剩余,这个电子填充在3a1轨道,因此磁矩为1µB.对于N缺陷的超胞体系,当去掉一个N原子之后,周围三个B原子会剩余三个未成键电子,三个电子依次填充在a′1和a′′1轨道上,导致超胞总磁矩也为1µB.这将在后面详细讨论.

从局域磁矩结果可以看出,所有原子的局域磁矩都很小,不到0.1µB,说明磁矩并不完全集中于原子上,而是主要分布于杂质原子附近的空间.另外与杂质原子最近邻的B原子上的磁矩为正,次近邻的N原子上的磁矩为负,而再次近邻的B原子上的磁矩又为正.自旋密度图给出了同样的结果.

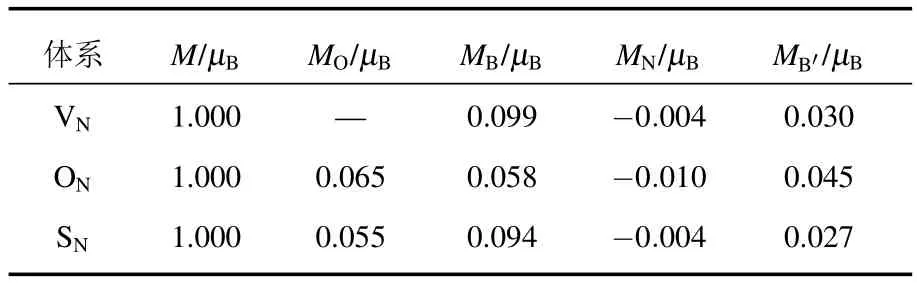
表2 不同掺杂体系的磁矩

3.2.2 自旋密度

从自旋密度图中可以直观看出体系的磁矩分布情况.三种体系的自旋密度如图2所示.其中图2(a)为具有N缺陷的BN单层的自旋密度,图2(b)为对应的侧视图;图2(c)是O掺杂时的自旋密度,图2(d)是对应的侧视图;图2(e)是S掺杂时的自旋密度,图2(f)是对应的侧视图.

图2 自旋密度 (a)氮缺陷顶视图;(b)氮缺陷侧视图;(c)氧掺杂顶视图;(d)氧掺杂侧视图;(e)硫掺杂顶视图;(f)硫掺杂侧视图

以O掺杂时的自旋密度图为例,可以看出磁矩主要分布于杂质原子附近的空间,并不完全集中于原子上,且掺杂的氧原子以及最近邻的三个B原子以及再次近邻的B原子上磁矩为正,而次近邻的N原子上磁矩为负.这与表2中局域磁矩数据一致.

3.3 电子结构

3.3.1 总态密度

图3给出了所研究体系的总态密度(DOS).其中图3(a)为未掺杂的BN单层,图3(b)为具有N缺陷的情况,图3(c)为O掺杂的情况,图3(d)为S掺杂的情况.从图3中可以看出,N缺陷以及掺杂体系中均产生了明显的杂质能级,而且杂质能级出现在禁带中,位置随着掺杂元素的不同而不同.对于未掺杂的h-BN,在费米能级处没有电子填充,是绝缘体,而且DOS完全对称,没有磁性;对于具有N缺陷的情况,在-0.34 eV(自旋向上)和0.35 eV(自旋向下)产生杂质能级,DOS出现不对称,因此体系具有磁性,而且杂质能级很窄,说明局域性较强,这与前面给出的自旋密度相一致,因为自旋密度图中磁矩主要分布在杂质原子附近.对于O掺杂的情况,杂质能级更靠近导带,出现在-0.22 eV(自旋向上)和0.23 eV(自旋向下);除了产生杂质能级,O掺杂的DOS与未掺杂的情况更为接近,因为结构变化很小.S掺杂情况的DOS与N缺陷情况相似,费米能级基本在导带和价带中间,杂质能级出现在0.35和-0.35 eV,但两者的成因本质上并不相同,后面将用分子轨道理论对上述结果进行详细解释.

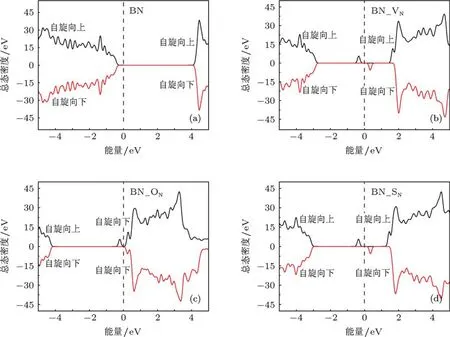
图3 总态密度 (a)未掺杂;(b)N缺陷;(c)O掺杂;(d)S掺杂

3.3.2 分子轨道分析及能带结构

由于O和S掺杂之后的BN单层具有C3V局域对称性,存在A1,A2和E三个不可约表示.A1,A2是一维的,而E是二维的.下面我们以分子轨道理论分析杂质能级和磁矩的形成原因.图4是O掺杂h-BN单层的杂质分子轨道示意图.

氧原子周围三个B的三个σ悬挂键构成A1和E两类不可约表示的基,通过对称匹配组合形成a1和e两个轨道,其中a1为一重简并,e为二重简并.氧原子的2s和2pz轨道构成不可约表示A1的基,杂化后形成2个a1轨道.而氧原子的2px和2py轨道构成不可约表示E的基,形成1个e轨道.同一类的三个A1不可约表示的群原子轨道线性组合成三个A1不可约表示的群分子轨道(1a1,2a1和3a1),两对E不可约表示的群原子轨道线性组合成两对E不可约表示的群分子轨道(1e和2e).按能量高低依次排列为1a1,1e,2a1,3a1,2e,共5个能级.由于O原子有6个价电子,3个B原子有3个未配对价电子,9个电子根据能量最低原理以及Pauling不相容原理排布,排满1a1,1e,2a1之后,剩余的一个电子排布在3a1.3a1位于禁带之中,就是在总态密度中看到的杂质能级的位置,这也同时解释了O,S掺杂的超胞总磁矩均为1µB.

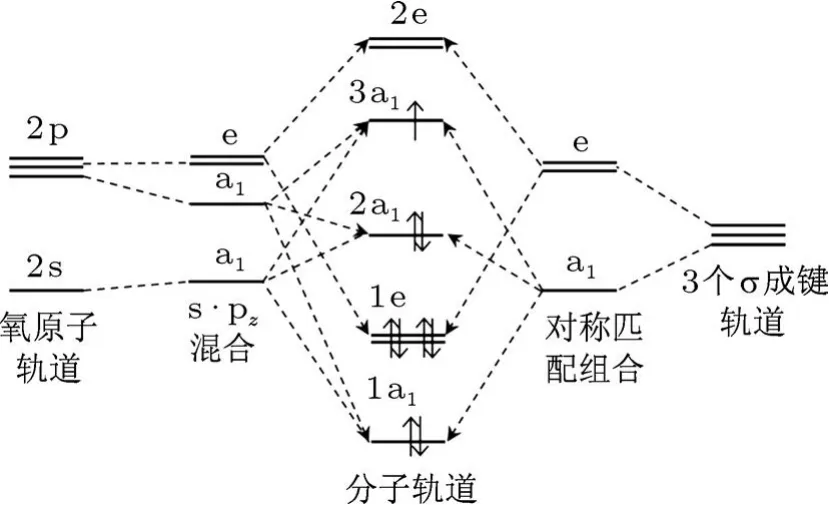
图4 O掺杂BN单层的杂质分子轨道示意图

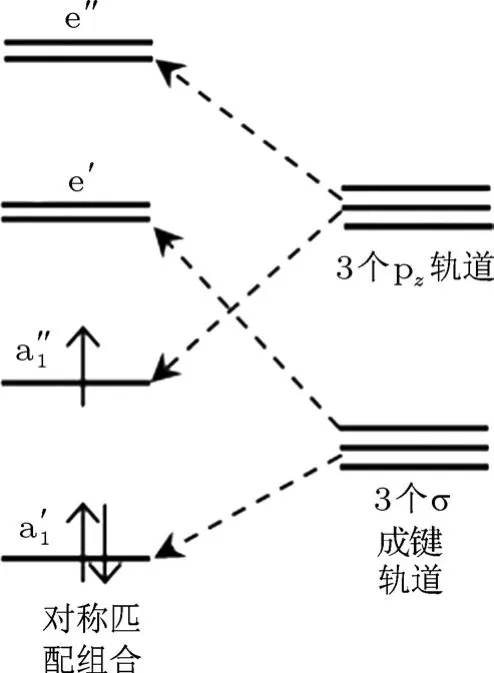
图5 具有N缺陷时的分子轨道

存在N缺陷时,局域对称性为D3h,图5给出了分子轨道示意图.3个B的3个σ键构成E′和两类不可约表示的基,通过对称匹配组合形成e′和两个轨道.而此时由于体系缺少一个N原子,相对于掺杂体系,电子结构发生更大变化,必须考虑3个B原子的3个pz轨道.与3个σ键类似,3个pz轨道构成 E′和两类不可约表示的基,通过对称匹配组合形成 e′和两个轨道.以上4个轨道能量的排列顺序为:体系中有3个未配对电子,其中两个电子排布在能级上,剩余的一个电子排布在能级上,能级位于禁带之中,这就解释了DOS中的杂质能级的产生,同时也说明总磁矩是1µB.

上面的分子轨道理论分析可以通过能带结构进一步证明.图6是O,S掺杂BN单层以及N缺陷的BN单层体系的能带结构.图6(a)和(b)中,对于O和S掺杂的体系,明确标注出了2e能级和3a1能级的位置.3a1能级相对平坦变化不大,表明局域性很强,与前面的讨论一致.图5中的1a1,1e,2a1这三个能级位于价带内,在图6中未标出.图6(c)中N缺陷的能级图明确标出了和e′这两个能级位置,能级较为平坦,局域磁矩很强,同样与前面的讨论一致.

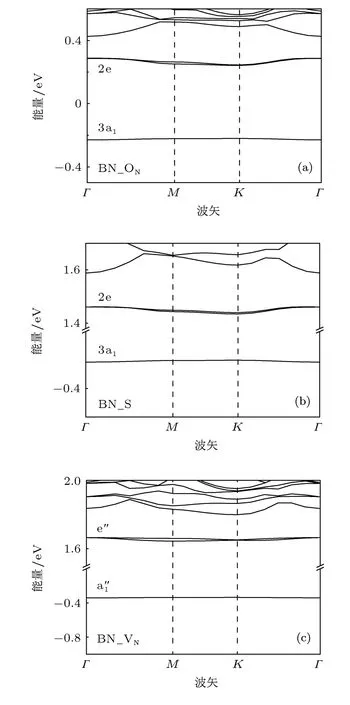
图6 能带结构图 (a)O掺杂;(b)S掺杂;(c)N缺陷

4 结论

采用第一性原理计算,研究了存在氮缺陷、氧取代氮、硫取代氮时h-BN的几何结构、磁性性质和电子结构.研究结果表明,存在N缺陷和O掺杂时体系的几何形变相对较小,S掺杂的体系的结构形变较大.三种体系的总磁矩都为1µB,局域磁矩和自旋密度图表明磁矩主要分布在缺陷附近的空间.三种体系的态密度图中都存在明显的杂质能级.利用分子轨道理论分析的结果表明,对于O/S掺杂情况,杂质分子轨道依次为1a1,1e,2a1,3a1,2e;对于含有氮缺陷的体系,杂质分子轨道依次为e′,e′.给出的能带结构与分子轨道分析相一致,说明了相关分析的合理性.

[1]Jin C H,Lin F,Suenaga K,Iijima S 2009 Phys.Rev.Lett.102 195505

[2]Loiseau A,Willaime F,Demoncy N,Hug G,Pascard H 1996 Phys.Rev.Lett.76 4737

[3]Blase X,Rubio A,Louie S G,Cohen M L 1994 Europhys.Lett.28 335

[4]Rubio A,Corkill J L,Cohen M L 1994 Phys.Rev.B 49 5081

[5]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004 Science 306 666

2.2.3 提取时间 在提取时间低于30 min时，艾渣总黄酮提取率随提取时间延长呈上升趋势，当提取时间为30 min时，提取率最高，为2.57%；提取时间30～50 min时，提取率随时间延长呈下降趋势，在50 min时降至最低，为2.19%；之后提取率又再次上升。原因可能是提取时间过短有效成分溶出不充分，而时间过长又导致杂质溶出过多，从而造成黄酮类化合物的结构发生转变。因此，提取时间选择30 min为最佳。

[6]Greber T e-J 2010 Surf.Sci.Nanotech.8 62

[7]Iijima S 1991 Nature 354 56

[8]Prinz G A 1998 Science 282 1660

[9]Jim´enez I,Jankowski A F,Terminello L J,Sutherland D G J,Carlisle J A,Doll G L,Tong W M,Shuh D K,Himpsel F J 1997 Phys.Rev.B 55 12025

[10]Lu D,Yang Y R,Xiao Y,Zhang X Y 2011 Chin.Phys.B 20 118101

[11]Xiao Q,Qiu G Z,Hu Y H,Wang D Z 2002 Acta Phys.Sin.51 2133(in Chinese)[肖奇,邱冠周,胡岳华,王淀佐2002物理学报51 2133]

[12]Wang G C,Yuan J M 2003 Acta.Phys.Sin.52 970(in Chinese)[王贵春,袁建民2003物理学报52 970]

[14]Nagashima A,Tejima N,Gamou Y,Kawai T,Oshirna C 1995 Phys.Rev.Lett.75 3918

[15]Jia J F,Wu H S 2006 Acta Phys.Chim.Sin.22 1520(in Chinese)[贾建峰,武海顺2006物理化学学报22 1520]

[16]Ooi N,Rairkar A,Lindsley L,Adams J B 2006 J.Phys.Condens.Matter 18 97

[17]Azevedo S,Kaschny J R,de Castilho C M C,de Brito Mota F 2007 Nanotechnology 18 495707

[18]Azevedo S,Kaschny J R,de Castilho C M C,de Brito Mota F 2009 Eur.Phys.J.B 67507

[19]Si M S,Xue D S 2007 Phys.Rev.B 75 193409

[20]Hohenberg P C,Kohn W 1964 Phys.Rev.136 864

[21]Kohn W,Sham L J 1965 Phys.Rev.140 1133

[22]Kresse G,Furthm¨uller J 1996 Phys.Rev.B 54 11169

[23]Wu F M,Fang Y Z,Meng X Q 2012 Chin.Phys.Lett.29 016801

[24]Niu X L,Deng Y F,Li X 2009 Acta Phys.Sin.58 7317(in Chinese)[牛雪莲,邓玉福,李雪2009物理学报58 7317]

[25]Zhou T G,Liu Z Q,Zuo X 2012 Chin.Phys.Lett.29 047503

[26]Ji Z H,Zeng X H,Cen J P,Tan M Q 2010 Acta Phys.Sin.59 1219(in Chinese)[季正华,曾祥华,岑洁萍,谭明秋2010物理学报59 1219]

[27]Kresse G,Joubert D 1999 Phys.Rev.B 59 1758

[28]Perdew J P,Burke K,Ernzerhof M 1996 Phys.Rev.Lett.77 3865

[29]Robertson J 1984 Phys.Rev.B 29 2131