级联参量振荡产生太赫兹辐射的理论研究*
李忠洋 邴丕彬 徐德刚 曹小龙 姚建铨
1)(华北水利水电学院电力学院,郑州 450011)
2)(天津大学精密仪器与光电子工程学院,激光与光电子研究所,天津 300072)
1 引言
太赫兹(THz)波是指频率在0.1-10 THz的电磁波,其波段介于毫米波和红外波之间.THz波在与物质相互作用时包含了丰富的物理和化学信息,因此THz波在物理、化学、光谱学、生命科学和天文学等基础研究领域,以及医学成像、材料检测、环境监测、射电天文、卫星通信和军用雷达等应用研究领域均具有重大的科学研究价值和广阔的应用前景[1-8].基于THz波参量振荡器(TPO)产生的THz波辐射源具有可调谐、相干、线宽窄、结构紧凑、室温运转等优点,近十年来得到了国内外广泛的重视[9-16].但从TPO的基本原理以及已报道的实验结果可以看出,由近红外的抽运光(约为1µm)抽运掺氧化镁铌酸锂(MgO:LiNbO3)晶体产生THz辐射,能量转换效率低于0.01%[17-19].提高THz波转换效率是THz辐射得以应用的关键.
光学参量效应产生THz波辐射的原理是:功率足够强的抽运光与晶体中同时具有红外活性和拉曼活性的晶格振动模耦合,激发出Stokes光子和电磁耦子,在电磁耦子色散曲线上小波矢处的受激电磁耦子散射就是THz波辐射.从THz波参量效应基本原理可以看出,提高THz波能量转换效率主要有以下几种方法:1)提高抽运光强度;2)使用波长更长的抽运光;3)降低增益介质对THz波的吸收.但这几种方法也各有不足:抽运光强度过高很容易损伤晶体,所以不能无限制地增加抽运光功率;中红外(3-10µm)抽运光虽然能增大THz波能量转换效率,但是中红外抽运光功率密度难以达到TPO阈值;由于MgO:LiNbO3晶体对THz波的吸收系数很大,1.5 THz处THz波吸收系数高达45 cm-1,THz波在MgO:LiNbO3晶体中传输0.5 mm能量损失91%[17].为了从实质上提高TPO产生THz波的转换效率,本文将探索一种新的THz波参量机理--THz波级联参量效应.
2 THz波级联参量效应原理
级联参量振荡的原理是:抽运光在周期极化铌酸锂(PPLN)晶体中参量振荡产生一阶信号光和一阶闲频光,此一阶信号光经过谐振腔放大再次抽运PPLN晶体产生二阶信号光和二阶闲频光,此二阶闲频光的频率处在THz波段.由于一阶和二阶信号光波长相近,通过合理设计谐振腔参数,可以同时满足二者振荡放大.经过放大的二阶信号光又一次抽运PPLN晶体产生三阶信号光和三阶闲频光,此三阶闲频光的频率也处在THz波段.同理,三阶信号光可以产生更高阶的THz辐射.若此过程一直延续下去,一个抽运光子可以产生多个THz光子,突破Manley-Rowe条件的限制,从而大大提高THz波的量子转换效率.
级联参量效应原理如图1所示.抽运光λp在PPLN晶体中满足前向参量过程,产生一阶信号光和一阶闲频光,如图1(a)所示.此过程满足能量守恒条件和动量守恒条件:
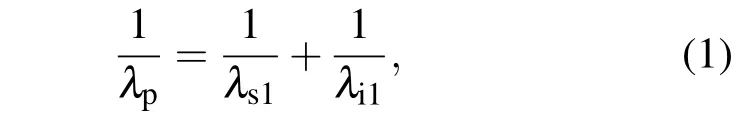
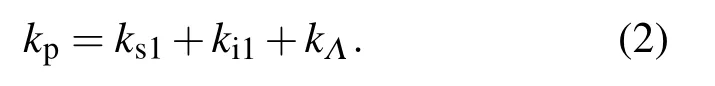
谐振腔中振荡放大的一阶信号光抽运PPLN晶体产生二阶信号光和二阶闲频光,此二阶闲频光的频率在THz波段.此过程可以同时满足两种相位匹配方式,前向参量过程满足相位匹配条件:
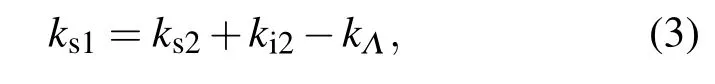
后向参量过程满足相位匹配条件:
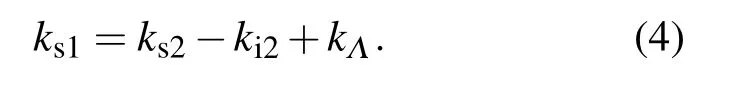
谐振腔中振荡放大的二阶信号光再一次抽运PPLN晶体,可以产生三阶信号光和三阶闲频光,此三阶闲频光频率也在THz波段.若此过程可以一直持续下去,从而一个抽运光子会产生多个THz波光子.
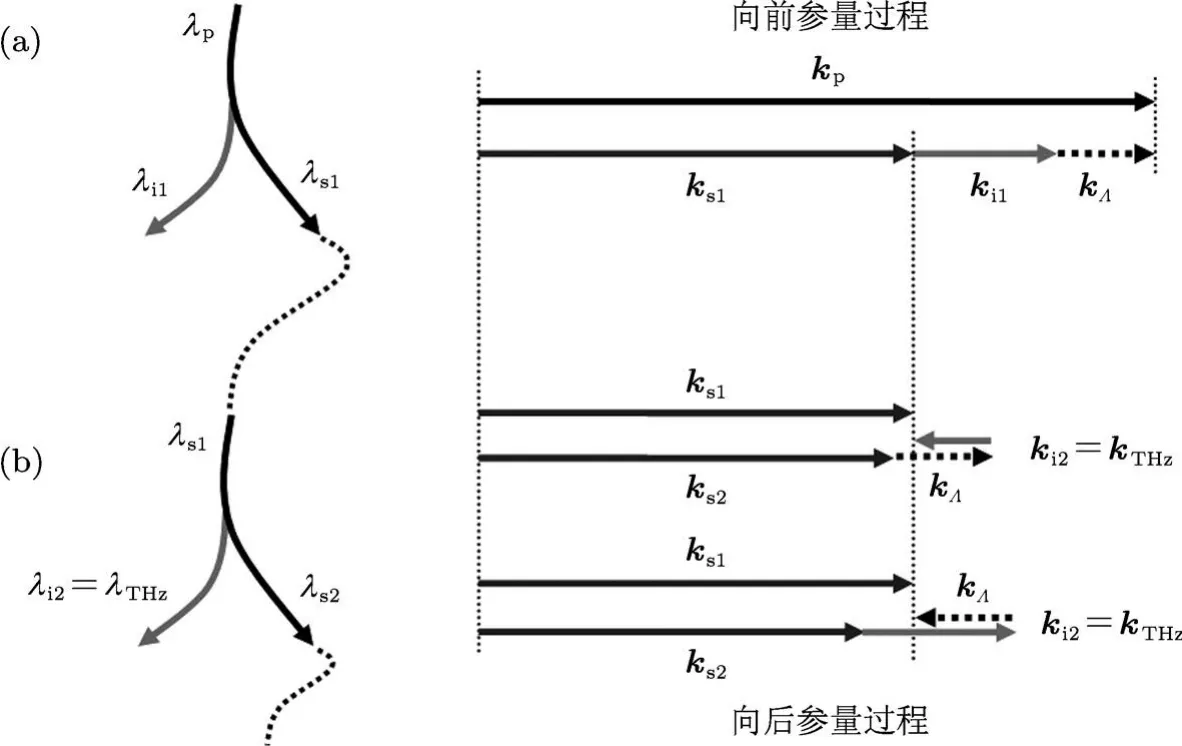
图1 级联参量效应示意图
3 PPLN晶体级联参量振荡产生频率调谐THz波的理论分析
3.1 一阶参量效应
基于光学参量振荡器产生THz辐射的优点之一就是可以通过改变相位匹配条件得到频率连续调谐输出的THz波.由(1)和(2)式可知,改变抽运波长,以及改变PPLN晶体极化周期、工作温度等参数可以改变相位匹配条件,进而可以得到频率调谐输出的一阶信号光.图2表示室温下一阶信号光和一阶闲频光的波长与抽运波长之间的变化关系,假设极化周期Λ=30µm.室温下MgO:LiNbO3晶体在红外波段和THz波段的折射率参考已报道的数据[20,21].抽运波长λp从1-1.96µm连续地调谐,可以得到一阶信号光的波长范围为1.5-3.85µm,一阶闲频光波长范围为2.12-4.73µm.在一阶参量振荡过程中,不但得到了频率调谐的一阶信号光,而且得到了宽调谐的一阶闲频光,即中红外辐射.频率调谐的一阶信号光可以得到频率调谐输出的THz波辐射.
图3表示室温下一阶信号光和一阶闲频光的波长与PPLN晶体极化周期之间的关系,假设λp=1064 nm.极化周期Λ从20-32.6µm连续地调谐,可以得到一阶信号光的波长范围为1.26-2.13µm,一阶闲频光波长范围为2.13-6.78µm.一阶信号光和一阶闲频光的波长对PPLN晶体极化周期的变化比较敏感,所以可以通过改变极化周期来得到调谐输出的一阶信号光和一阶闲频光.
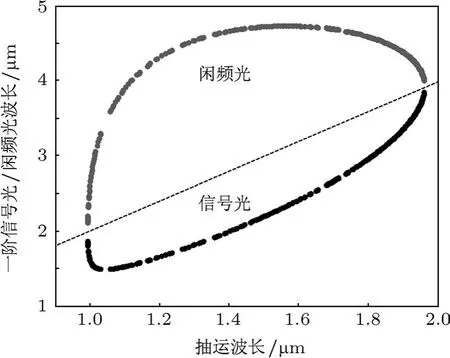
图2 室温下一阶信号光和一阶闲频光的波长与抽运波长之间的关系,Λ=30µm
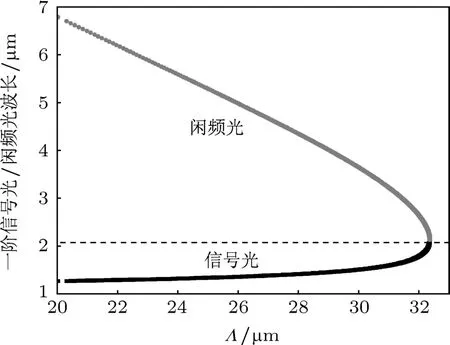
图3 室温下一阶信号光和一阶闲频光的波长与PPLN晶体极化周期Λ之间的关系,λp=1064 nm
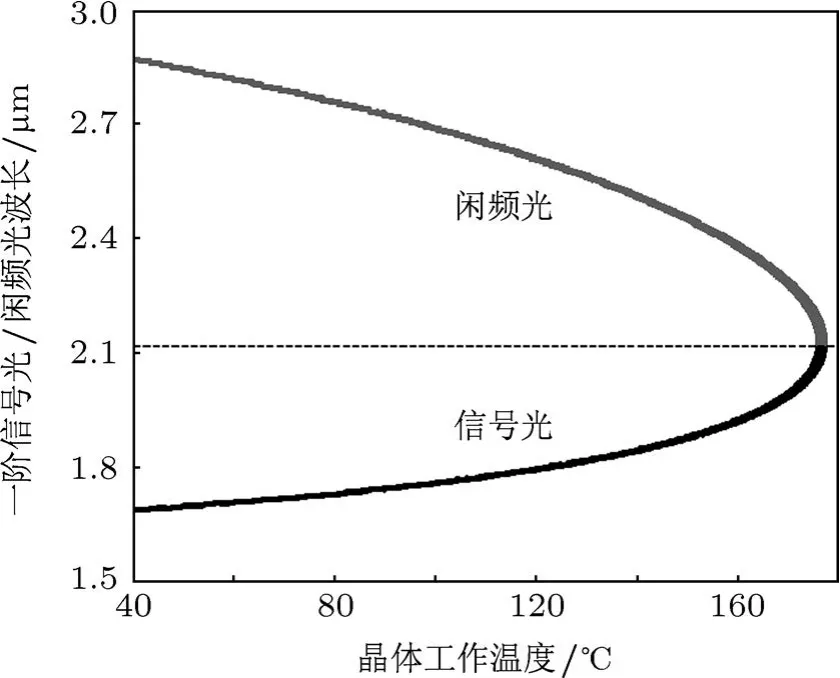
图4 一阶信号光和一阶闲频光的波长与PPLN晶体工作温度之间的关系,λp=1064 nm,Λ=31.6µm
改变PPLN晶体的工作温度可以改变抽运光、各阶信号光和各阶闲频光的折射率,从而改变相位匹配条件以得到频率调谐输出的光辐射.图4表示一阶信号光和一阶闲频光的波长与PPLN晶体工作温度之间的关系,λp=1064 nm,Λ=31.6µm.晶体温度范围为40-177.3◦C,得到一阶信号光的波长为1.69-2.13µm,对应一阶闲频光波长为2.13-2.87µm.
3.2 二阶参量效应
由(3)和(4)式可知,改变一阶信号光波长,以及改变PPLN晶体极化周期、工作温度等参数可以改变相位匹配条件,进而可以得到频率调谐输出的二阶闲频光,也就是THz辐射.图5表示室温下当PPLN晶体极化周期Λ=20µm时THz波频率与一阶信号光波长之间的关系.当一阶信号光波长范围在1-2µm变化时,后向级联参量效应得到的THz波频率范围在2.056-2.067 THz,前向级联参量效应得到的THz波频率范围在4.268-4.478THz.THz波的频率调谐幅度很小,所以在PPLN极化周期固定不变的情况下,通过改变一阶信号光的波长并不能得到宽调谐输出的THz波.
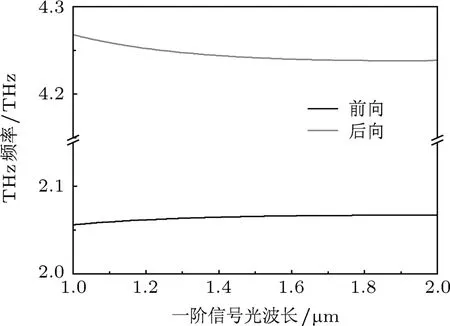
图5 室温下THz波频率与一阶信号光波长之间的关系,Λ=20µm
图6表示室温下THz波频率与PPLN晶体极化周期Λ之间的关系,λs1=1.55µm.极化周期变化范围为10-80µm,得到后向参量过程产生的THz波频率范围为0.52-3.80 THz,前向参量过程产生的THz波频率范围为1.30-6.17 THz.在一阶信号光波长固定时,THz波频率对PPLN晶体极化周期变化较敏感,通过二阶前向和后向参量过程,可以得到范围在0.52-6.17 THz的宽调谐THz波输出.
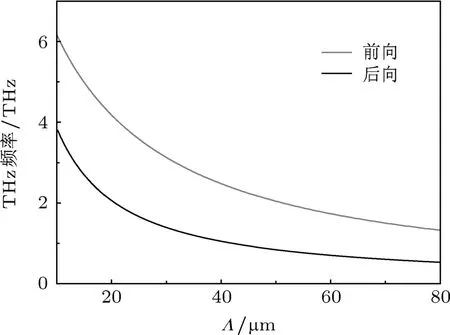
图6 室温下THz波频率与PPLN晶体极化周期Λ之间的关系,λs1=1.55µm
图7表示THz波频率与PPLN晶体工作温度之间的关系,λs1=1.55µm,Λ=30µm.晶体温度范围为40-170◦C,得到后向参量过程产生的THz波频率范围为1.344-1.385 THz,前向参量过程产生的THz波频率范围为3.016-3.112 THz.THz波在PPLN晶体中的折射率随温度的变化情况参考已报道数据[22].改变工作温度对THz波频率调谐影响很微小.但值得注意的是,在PPLN晶体中受激散射产生THz波的过程中,温度的改变会影响晶格振动线宽.温度降低会导致晶格振动线宽变窄[23],THz波的增益系数变大.而且随着振动线宽的变窄,PPLN晶体对THz波的吸收系数变小,所以PPLN晶体应工作在较低温度下以得到高功率的THz波辐射.
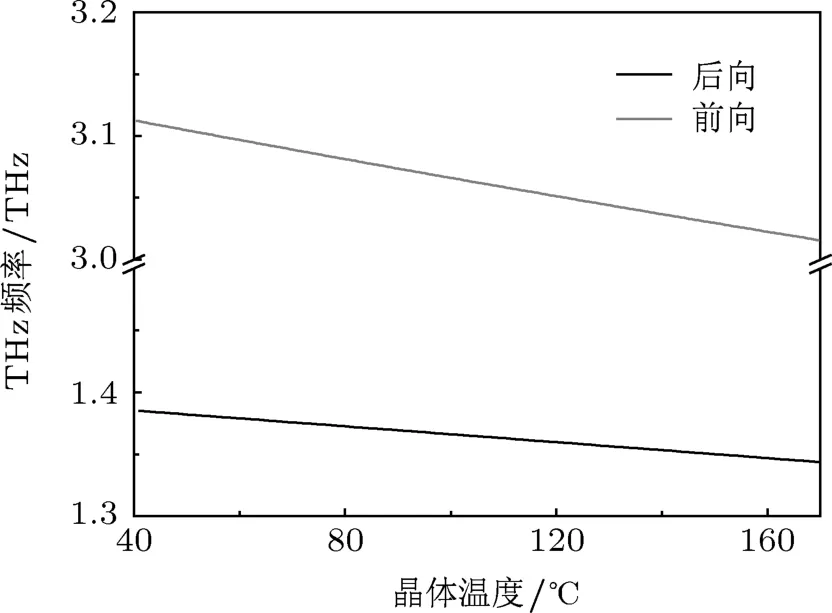
图7 THz波频率与PPLN晶体温度之间的关系,λs1=1.55µm,Λ=30µm
4 PPLN晶体级联参量振荡产生THz波的增益分析
PPLN晶体中利用准相位匹配技术可以有效地增大抽运光、信号光、闲频光之间的相互作用,从而提高THz波的转换效率.根据已报道文献推导出的非共线相位匹配条件下THz波在MgO:LiNbO3晶体中的增益和吸收表达式[24],推导了二阶参量振荡过程中,三波共线振荡产生THz波的增益和吸收表达式:
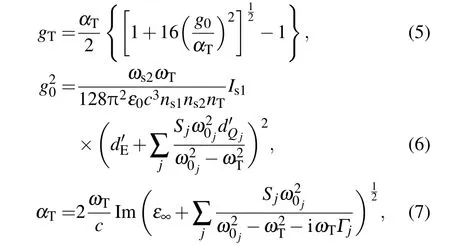
其中g0为低损耗极限情况下的参量增益,αT为THz波在频率ωT处的吸收系数,ns1,ns2,nT分别为二阶参量过程中一阶信号光、二阶信号光和THz波的折射率,Is1为一阶信号光抽运功率密度,=16πd33与二阶非线性参量过程有关,
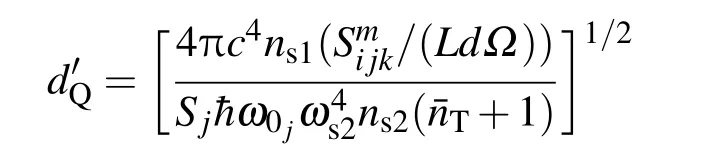
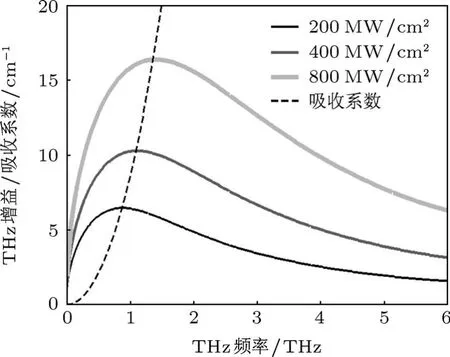
图8 THz波增益系数和吸收系数与THz波频率之间的关系,λs1=1.55µm,抽运功率密度Is1分别为200,400,800 MW/cm2
5 PPLN晶体级联参量振荡产生THz波的实验设计
根据前述分析,PPLN晶体对THz波的吸收系数很大,所以采用浅表垂直输出方式耦合输出THz波,可以极大减少PPLN晶体对THz波的吸收,从而可以有效提高THz波输出功率.PPLN晶体可以满足抽运光、信号光和闲频光三者共线振荡,有效增大三者间的相互作用体积,从而提高光学转换效率.级联参量振荡可以有效重复利用抽运光子,从而提高THz波量子转换效率.基于以上分析,设计了PPLN晶体级联参量振荡产生THz波的实验,如图9所示.抽运源采用分布反馈掺镱光纤激光器,功率为20 mW,波长为1064 nm,线宽小于100 kHz[25,26],经过MOPA系统放大可以输出15 W功率.抽运光经过非球面镜准直,经过光学隔离器,聚焦到PPLN晶体中心,聚焦点尺寸为100µm.谐振腔有两片凹透镜M1,M2和两片平面镜M3,M4组成.所有腔镜对信号光镀全反膜,M1和M2对抽运光高透.抽运光在PPLN-1晶体中参量振荡产生一阶信号光和一阶闲频光,一阶信号光在谐振腔中振荡放大,在PPLN-2晶体中经前向和后向参量过程产生二阶信号光和THz辐射.谐振腔中抛物面镜中心钻一个直径在1 mm的小孔,允许各阶信号光通过,THz波经抛物面镜反射耦合输出.由于THz波的孔径比各阶信号光大,所以经过小孔THz波能量不会损失很大.THz波的功率经过斩波器后可以通过GOLAY CELL探测器测得.腔镜M4可以换成对各阶信号光5%透过率的镜子,用以测量各阶信号光的频率,进而可以通过能量守恒原理计算出THz波的频率.改变PPLN晶体的温度和极化周期可以得到频率调谐输出的THz辐射.本实验可以实现高效率、宽调谐、窄线宽、小型化、室温运转、连续THz辐射源,满足其在高分辨率光谱学、传感技术、远程通信等领域的应用.
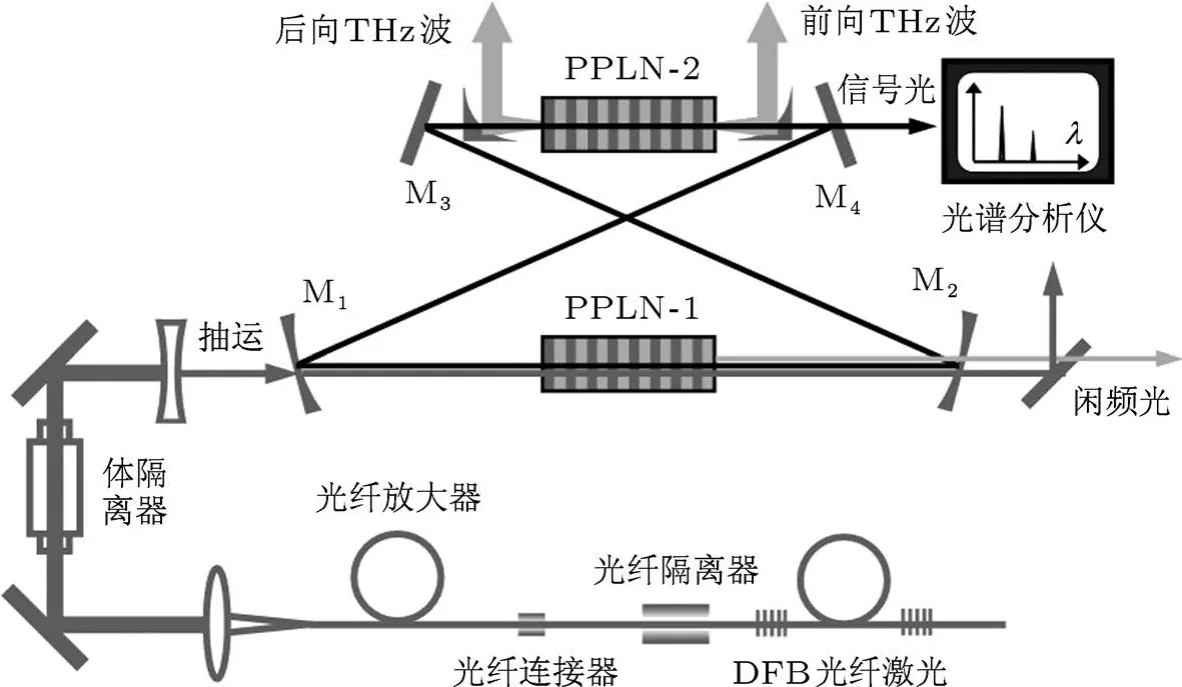
图9 级联参量振荡实验示意图
6 结论
本文提出了级联参量振荡产生THz波的新机理.以PPLN晶体为例,分析了抽运光波长、PPLN晶体极化周期和工作温度对产生一阶、二阶闲频光频率的影响.室温下当λp=1064 nm时,极化周期Λ从20-32.6µm连续地调谐,可以得到范围为2.13-6.78µm宽调谐中红外辐射.在一阶信号光波长λs1=1.55µm时,极化周期的范围为10-80µm,通过二阶前向和后向参量过程,可以得到范围在0.52-6.17 THz的宽调谐THz辐射.推导了三波共线相互作用情况下THz波的增益特性和吸收特性.基于分析结果,设计了以单频连续全光纤激光器作为抽运源,在PPLN晶体中级联参量振荡产生高效率、宽调谐、窄线宽、小型化、室温运转、连续THz辐射源的实验.
[1]Ferguson B,Zhang X C 2002 Nature Mater.1 26
[2]Tonouchi M 2007 Nat.Photon.1 98
[3]Alexandrov B S,Gelev V,Bishop A R 2010 Phys.Lett.A 374 1214
[4]Tian L,Zhou Q L,Zhao K,Shi Y L,Zhao D M,Zhao S Q,Zhao H,Bao R M,Zhu S M,Miao Q,Zhang C L 2011 Chin.Phys.B 20 010703
[5]Wang Y,Minamide H,Tang M 2010 Opt.Express 18 15504
[6]Hirata A,Takahashi H,Yamaguchi R J,Kosugi T,Murata K,Nagatsuma T,Kukutsu,Kado Y 2008 J.Lightwave Technol.26 2338
[7]Sanchez A R,Zhang X C 2008 IEEE J.Sel.Top.Quantum Electron.14 260
[8]Wu L,Ling F R,Zuo Z G,Liu J S,Yao J Q 2012 Chin.Phys.B 21 017802
[9]Li Z Y,Yao J Q,Li J,Bing P B,Xu D G,Wang P 2010 Acta Phys.Sin.59 6237(in Chinese)[李忠洋,姚建铨,李俊,邴丕彬,徐德刚,王鹏2010物理学报59 6237]
[10]Minamide H,Ikari T,Ito H 2009 Rev.Sci.Instrum.80 123104
[11]Ikari T,Guo R,Minamide H 2010 J.Eur.Opt.Soc.Rap.Pub.5 10054
[12]Li Z Y,Yao J Q,Xu D G 2011 Chin.Phys.B 20 054207
[13]Guo R,Akiyama K,Minamide H 2006 Appl.Phys.lett.88 091120
[14]Hayashi S,Shibuya T,Sakai H 2009 Appl.Opt.48 2899
[15]Stothard D J M,Edwards T J,Walsh D 2008 Appl.Phys.Lett.92 141105
[16]Walsh D,Stothard D J M,Edwards T J 2009 J.Opt.Soc.Am.B 26 1196
[17]Molter D,Theuer M,Beigang R 2009 Opt.Express 17 6623
[18]Walsh D A,Browne P G,Dunn M H 2010 Opt.Express 18 13951
[19]Kiesling J,Fuchs F,Buse K 2011 Opt.Lett.36 4374
[20]Barker A S,Jr,Loudon R 1967 Phys.Rev.158 433
[21]Gayer O,Sacks Z,Galun E,Arie A 2008 Appl.Phys.B:Lasers Opt.91 343
[22]Sowade R,Breunig I,Tulea C,Buse K 2010 Appl.Phys.B 99 63
[23]Johnston W D,Kaminow Jr I P 1968 Phys.Rev.168 1045
[24]Sussman S S 1970 Stanford Univ.Microwave Lab.1851 22
[25]Jeong Y,Nilsson J,Sahu J K,Horley D N,Hickey R 2007 IEEE J.Sel.Top.Quantum Electron.13 546
[26]Jeong Y,Boylang A J,Sahu J K 2009 J.Opt.Soc.Korea 13 416

