双势阱中能级分裂的物理机理探析
段艳涛,徐永刚,林钱兰,安 斓,林富锟,朱海飞,李永放,郭建中
(陕西师范大学 物理学与信息技术学院,陕西 西安710062)
纳米结构器件的超小尺寸和优良的性能引起了很多研究者的注意[1].人们通过能量量子化在这些器件之中实现了对有效带隙的可调谐性,由此获得许多新的电子和光电子特性[2-3].许多这样的量子效应器件已经有了商业化产品,例如,多重量子阱(Multiple Quantum Well,MQW)结构制成的功能型器件,共振遂穿二极管(Resonant Tunneling Diodes,RTD),共振遂穿晶体管(Resonant Tunneling Transistors,RTT),量子级联激光器(Quantum Cascade Lasers,QCL),量子阱红外光探测 器 (Quantum Well Infrared Photodetectors,QWIP),量子限制斯塔克效应调制器(Quantum Confined Stark Effect Modulators,QCSEM)等.其中量子级联激光器(Quantum Cascade Lasers,QCL)是宽带和可调谐激光的首选[4-6],共振遂穿二极管(RTD)和共振遂穿晶体管(RTT)可用于多值数字逻辑和负阻抗器件[7-8],量子阱红外光探测器(QWIP)可用于夜视仪,非损伤医学诊断、环境污染检测[9-14]等.
在半导体共振遂穿器件中,双势阱是一个基本结构单元.电子在系统中的传输问题可以通过薛定谔方程或转移矩阵的方法来描述.然而,在双势阱中的能态分裂又是这一基本结构单元中的最基本的问题.如何理解能态分裂的物理原因或机理,如何从简单易懂的物理图像认识这一问题则是研究量子器件者们更为关注的问题.本文利用转移矩阵的方法,研究双势阱中不同区域内电子动量之间的耦合问题,以更为直观的图像,从新的角度解释、分析能态分裂的特性和物理机理.这一结果对于理解双势阱、多势阱组合构成的复杂器件中波矢量的传输机理具有一定的参考价值.
1 模型与理论分析
最基本的一维双势阱结构如图1所示,电子的能量与系统中的势垒和势阱之间满足关系:V1<E<V2<V0.系统中电子在各个区间的波函数分别为[15]
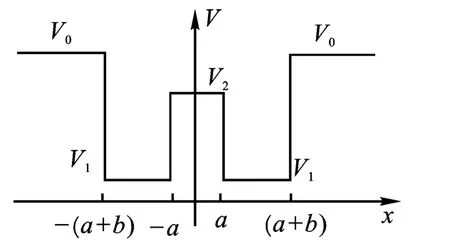
图1 一维方形双势阱Fig.1 Schematic of one-dimensional square double potential well


在势垒中的转移矩阵为[15]

1.1 势阱两边的波矢量p0与势阱中的波矢量k1之间的关系
依据转移矩阵,波函数ψ(x)及其一阶导数ψ′(x)应满足的矩阵方程为


由(1)式可以得到

利用向量(-p01)左乘(4)式两边并将(5)式代入,可以化简为

其中:

令(-p01)M(b)=(-p1d)和M(b)(1 -p0)T=(d -p1)T.这样可以得到:

前一个式子说明,电子从左边进入到势阱之中时产生一个新的波矢p1,它是入射的波矢量p0与势阱中的k1矢量叠加的结果.第二个关系则表明p0与k1两个波矢量之间应该满足的约束关系.利用矢量叠加图可以清楚的表示新的波矢量p1与p0和k1的关系,如图2a所示.这一结果说明入射电子的波矢量与势阱中的波矢量之间是通过相位k1b因子将其分解为沿传播方向和垂直于传播方向的两个部分的叠加,p1与p0和k1的分量在传播方向上满足动量守恒关系.用向量(d p1)T右乘(-p01)M(b)式,可得
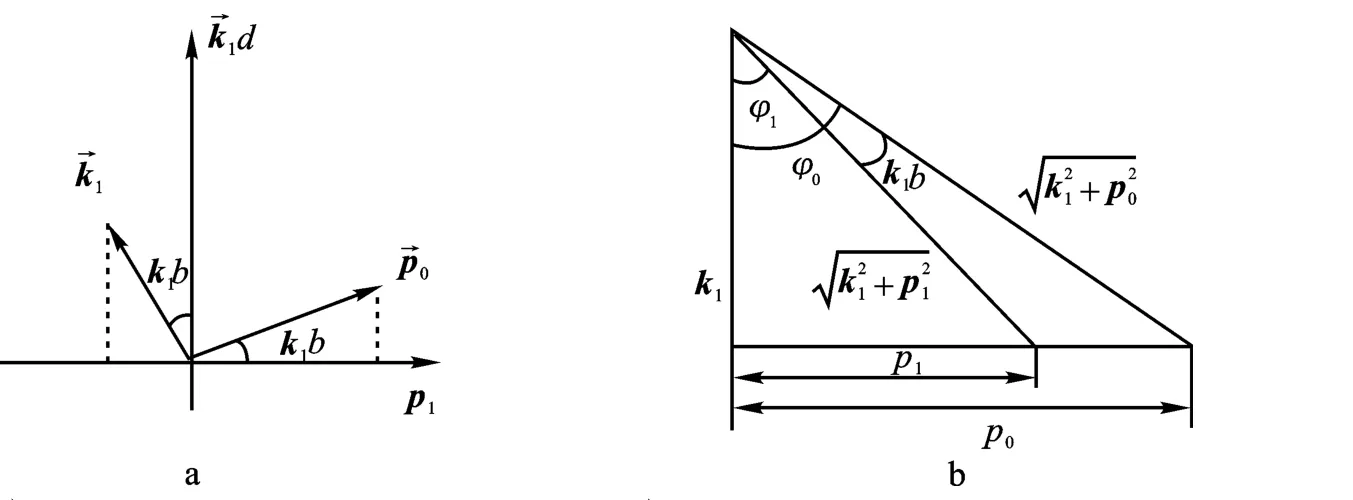
图2 →p0与→k1的矢量叠加产生了新的波矢量→p1(a),角度φ0和φ1以及k1b关系图(b)Fig.2 The new wave vector→p1is the vector superposition between→p0and→k1(a),The angular relation amongφ0,φ1and k1b(b)

对向量进行归一化,可令d=1,则(7)式可表示为tan(k1b)=tan(φ0-φ1),其中,tanφ0=p0/k1,tanφ1=p1/k1.进一步可得
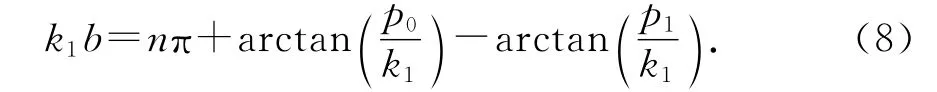
图2b表示了(8)式中各个角度φ0=φ1+k1b和φ0=arctan(p0/k1)以及φ1=arctan(p1/k1)之间的关系.当取n=0时,有φ1=φ0-k1b.可见p1仅是p0的一部分.后面将会看到p1会与势垒中的波矢量k2之间产生相干叠加,从而导致在双势阱中的能态产生分裂.
1.2 波矢量p1与势垒中的波矢量k1之间的关系利用(-p0 1)M(b)=(-p1 d)和

将M(2a)代入上式后化简为:

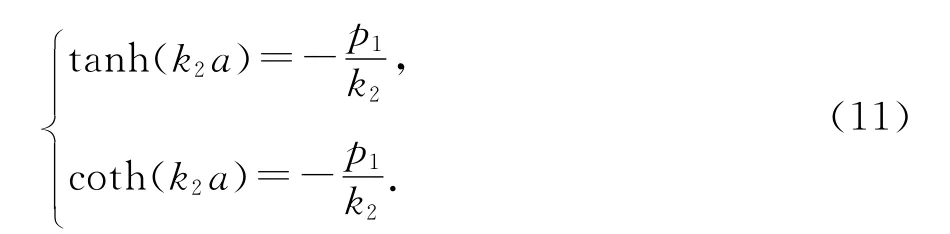
由于tanh(k2a)≠coth(k2a),说明这两种表示都与电子在系统中存在的状态相联系.在系统存在两种模式的波,或者说能态是分裂的.将(11)式变形后得

带入到k1b=之中,可得到双势阱中的本征方程为

其中Δφ=φ2-φ2′,φ2==arctanφ2′.两个本征值方程进一步说明在双势阱系统中存在着两种模式的波.n=0时的(12)式中的角度分布关系,如图3所示.图中的两个直角三角形共用一个

图3 双势阱系统的波矢量之间的关系Fig.3 The relation between wave vectors in double potential well
直角边,它的边长为k1.若V1=0,这时为入射电子的能量),k1越大,φ2或φ2′越小.同时比较p2和p2′,当k2a越大,两者的差越大,如图4(b)所示.波矢量差Δp=p2-p2′是非线性变化,势垒宽度越大,Δp越小,它随着入射电子能量的增加呈单调增长规律.
2 结果分析
根据前面对波矢量的定义:p0=.假设m=1,ħ=1,V1=0,V2=1.当入射电子的能量增加时,则Δ=p2-p2′增加,这意味着在系统中的能量分裂会增加.根据ε=(ħk)2/2m,可以得到能级分裂Δε=[(ħp2)2-(ħp2′)2]/2m,结果如图4所示.

图4 对应不同势垒宽度时的能级分裂(a)和波矢量差随入射电子能量的变化(b)Fig.4 The energy level splittings corresponding to different barrier widths(a),The electron energies dependence of difference of wave vectors(b)
从图中可以看到,势垒越窄,能态分裂越大;对应一定的势垒宽度,随着入射电子的能量增加能级分裂有一个最大值.势垒宽度愈大,最大值所对应的电子能量越大,所以当入射电子能量大于最佳值之后,能级分裂随入射电子能量增大而变小.
从量子物理的层面上理解:当势垒宽度较小时,电子容易遂穿过去到达另一边的势阱之中,与其中的电子波函数耦合.遂穿几率越大,波函数之间的耦合越强,能态的分裂会越大,反之波函数之间的耦合越弱,能态分裂越难.因此在势阱的底部能态分裂要小于势阱的顶部.能态分裂的最大值对应着图4a中的曲线弯曲部分所对应的能量.势垒宽度越小,则最大处的能量越低.因此这一结论对于研究利用双势阱系统制备量子器件具有一定的意义.
3 结论
本文以电子在双势阱中传播的波矢量耦合的方式和直观的物理图像解释了能态在系统中产生分裂的物理机理.从量子物理的层面解释了势垒宽度对能态分裂的影响.所得结果对于理解半导体双势阱结构中的能态分布和制备具有实际意义的量子器件具有一定的参考价值.
[1]Goser K,Glosekotter P,Dienstuhl J.Nanoelectronics and nanosystems:from transistors to molecular and quantum devices[M].Berlin:Springer,2004.
[2]Bhattacharyya S,Das N R,Sen S.Electrical tuning of intersubband transition in a semiconductor quantum ring[J].Journal of Applied Physics,2009,105:053108.
[3]Bismuto A,Terazzi R,Beck M,et al.Electrically tunable,high performance quantum cascade laser[J].Applied Physics Letter,2010,96:141105-141108.
[4]Wittmann A,Gresch T,Gini E,et al.High-performance bound-to-continuum quantum-cascade lasers for broad-gain applications[J].IEEE Journal of Quantum Electronics,2008,44:36.
[5]Yao Y,Charles W O,Tsai T,et al.Broadband quantum cascade laser gain medium based on a“continuumto-bound”active region design[J].Applied Physics Letter,2010,96:211106-211109.
[6]Fujita K,Edamura T,Furuta S,et al.High-performance homogeneous broad-gain quantum cascade lasers based on dual-upper-state design[J].Applied Physics Letter,2010,96:241107-241110.
[7]Worschech L,Hartmann F,Kim T Y,et al.Universal and reconfigurable logic gates in a compact three-terminal resonant tunneling diode[J].Applied Physics Letter,2010,96:042112-042115.
[8]Hinata K,Shiraishi M,Suzuki S,et al.Sub-terahertz resonant tunneling diode oscillators with high output power(200μW)using offset-fed slot antenna and high current density[J].Applied Physics Express,2010,3:014001-014003.
[9]Eker S U,Kaldirim M,Arslan Y,et al.Large-format voltage-tunable dual-band quantum-well infrared photodetector focal plane array for third-generation thermal imagers[J].IEEE Electron Device Letter,2008,29:1121.
[10]Liu H C.Dependence of absorption spectrum and responsivity on the upper state position in quantum well intersubband photodetectors[J].Journal of Applied Physics,1993,73:3062-3067.
[11]Gunapala S D,Levine B F,Pfeiffer L,et al.Dependence of the performance of GaAs/AlGaAs quantum well infrared photodetectors on doping and bias[J].Journal of Applied Physics,1991,69:6517-6520.
[12]Lhuillier E,Pere-Laperne N,Ribet-Mohamed I,et al.Quantum well infrared photodetectors hardiness to the nonideality of the energy band profile[J].Journal of Applied Physics,2010,107:123110-123117.
[13]Kukkonen C A,Sirangelo M N,Chehayeb R,et al.Commercialization of quantum well infrared photodetector focal plane arrays[J].Infrared Physics and Technology,2001,42:397-405.
[14]Schneider H,Liu H C,Winnerl S,et al.Terahertz two-photon quantum well infrared photodetector[J].Optics Express,2009,17:12279-12284.
[15]曹庄琪.波导光学[M].北京:科学出版社,2007:254-256.

