三角代数上的广义高阶Jordan导子

马 飞，张建华，任刚练

（1陕西师范大学 数学与信息科学学院，陕西 西安，710062；2咸阳师范学院 数学与信息科学学院，陕西 咸阳，712000）

设A是任意代数，称M是其A－双模，若满足对于任意的A∈A，M∈M，有AM、MA∈M．一个可加映射d：A→M称为导子、Jordan导子或者Jordan三重导子，如果d满足对于任意的A、B∈A，有d（AB）＝d（A）B＋Ad（B），d（A2）＝d（A）A＋Ad（A）或者d（ABA）＝d（A）BA＋Ad（B）A＋ABd（A）成立．一个可加映射f：A→M称为广义导子或广义Jordan导子，如果存在导子或Jordan导子d：A→M使得对于任意的A、B∈A，有f（AB）＝f（A）B＋Ad（B）或f（A2）＝f（A）A＋Ad（A）．近年来，各种算子代数上使得一个线性映射成为（Jordan）导子和广义（Jordan）导子的研究工作不断出现，引起了许多学者的兴趣．显然，（广义）导子一定是（广义）Jordan导子，反之一般不成立［1］．自然的一个问题就是在哪些代数上的（广义）Jordan导子是（广义）导子？1957年，Herstein首先在文献［2］中证明了每个2－非挠半素环上的Jordan导子是导子；随后有很多结果被证明，文献［3－4］证明了每个三角代数和套代数上的Jordan导子是导子；文献［5］证明了每个套代数上的广义Jordan导子是广义导子；我们在文献［1］中证明了每个上三角代数到其双模上的广义Jordan导子是一个广义导子与反导子的和．类似结果可见文献［6－8］．

另外，高阶导子也得到很多学者研究（见文献［9－11］）．下面先给出定义：

定义1［9］设D＝（di）i∈N是环R上满足d0＝idR的一族可加映射．称映射D为高阶导子（简记为HD），如果对于任意的A、B∈R，有dn（AB）＝映射D称为高阶Jordan导子（简记为HJD），如果对于任意的A∈R，有dn（A2）＝；映射D称为高阶Jordan三重导子（简记为HJTD），如果对任意的A、B∈R，有

定义2设F＝（fi）i∈N是环R上满足f0＝idR的一族可加映射．映射F称为广义高阶导子（记为GHD），如果存在R上的高阶导子D＝（di）i∈N，使得对于任意的A、B∈R有fn（AB）＝映射F称为广义高阶Jordan导子（简记为GHJD），如果存在R上的高阶Jordan导子D＝（di）i∈N，使得对于任意的A∈R，有fn（A2）＝；映射F称为广义高阶Jordan三重导子（简记为GHJTD），如果存在R上的高阶Jordan三重导子D＝（di）i∈N，使得对任意的A、B∈R有

文献［9］证明了每个2－非挠半素环上的高阶Jordan导子是高阶Jordan导子；文献［10］证明了三角代数上的高阶Jordan导子是高阶导子．自然就产生这样的一个问题：每个三角代数上的广义高阶Jordan导子是不是广义高阶导子？本文就从这个角度出发来回答这个问题．

三角代数首先是在文献［12］中引出，随后被许多学者研究［4，10－15］．设A和B是可交换R上的代数，且分别含有单位元IA和IB，M是忠实的含单位（A，B）－双模．M称为忠实的A－左（右）模是指如果A∈A且AM＝0（MA＝0），则有A＝0．一个在通常矩阵算法意义下的R－代数

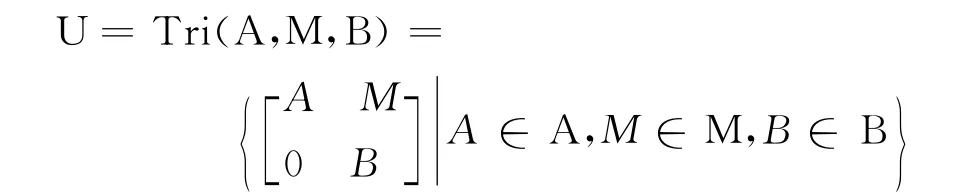
称为三角代数．有关三角代数最典型、也是最重要的模型是上（下）三角矩阵代数和套代数．

显然，三角代数U存在非平凡幂等元e1和e2，其中

显然三角代数是含有单位元I的：I＝e1＋e2．由矩阵的运算可知，对于任意的1≤i≤j≤2，有Uij＝eiUej．因而可以将三角代数U表示为

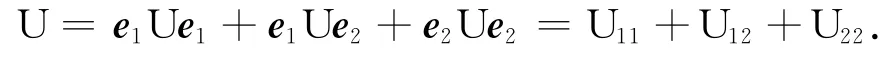
本文假设所有的映射都是可加的，N表示包含0的自然数集．

由文献［10］可知，每个高阶Jordan导子是高阶导子，因此本文中总假设是高阶导子即可．

类似于文献［9］的证明可得下面的引理：

引理1 设U＝Tri（A，M，B）是三角代数，D＝（di）i∈N是高阶导子，F＝ （fi）i∈N是GHJD，则对于任意的A、B、C∈U，都有

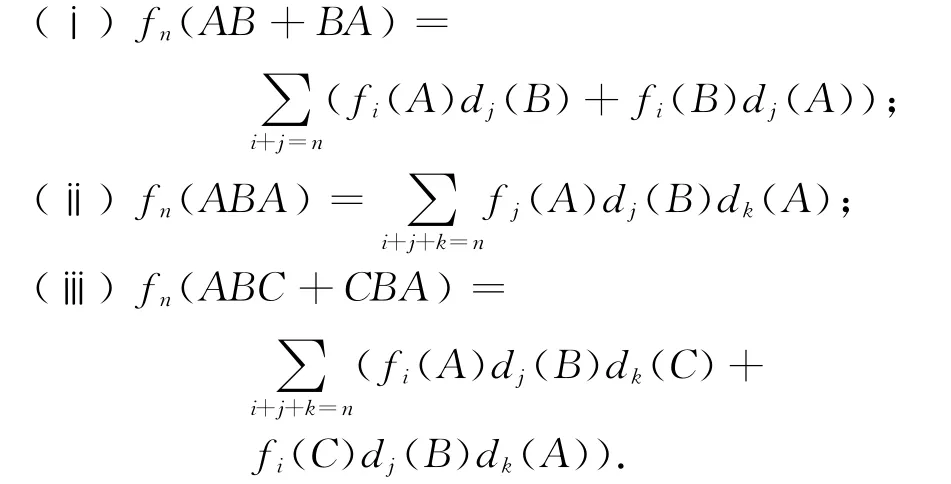
特别地，当n＝1时，由GHJD的定义可知f1是广义Jordan导子［15］．

引理2［15］设A、B是2－非挠可交换环R上的含单位代数，M是（A，B）－双边模且U＝Tri（A，M，B）是三角代数，则U上的每个广义Jordan导子都是广义导子．

引理3 设f1是广义Jordan导子，d1是Jordan导子，则当i＝1，2时，有

（ⅰ）d1（e1）∈U12，d1（e2）∈U12，d1（U12）⊆

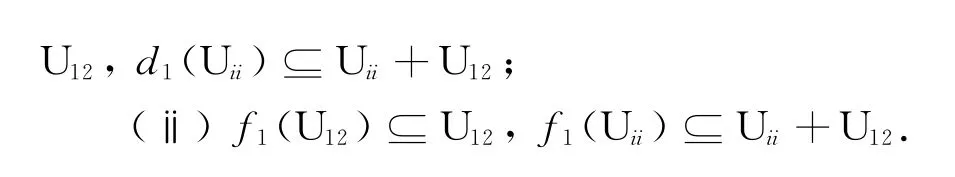
证明 （ⅰ）因为三角代数上的Jordan导子是导子［4］，因而d1是导子．注意到在三角代数中，e2e1＝e2Ue1＝0，ei＝e2i，且d1（e1）＝d1（e1）e1＋e1d1（e1），因而

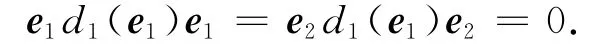
因此，d1（e1）∈U12．又因为d1（I）＝0，所以d1（e2）＝－d1（e1）∈U12．

对于任意的A12∈U12，由A12＝e1A12＝A12e2可知：

由d1（e1）∈U12，d1（e2）∈U12，则d1（A12）＝e1d1（A12）＝d1（A12）e2．于是

对于任意的A11∈U11，A22∈U22，则由d1（A11）＝d1（A11）e1＋A11d1（e1）知：e2d1（A11）e2＝0，因此d1（A11）∈U11＋U12．

类似可以证明d1（A22）∈U22＋U12．

（ⅱ）由于f1是广义Jordan导子，则

f1（e1）＝f1（e1）e1＋e1d1（e1）∈U11＋U12；f1（e2）＝f1（e2）e2＋e2d1（e2）∈U22＋U12．对于任意的A12∈U12，由引理1（ⅰ）可得

f1（A12）＝f1（e1A12＋A12e1）＝f1（e1）A12＋e1d1（A12）＋f1（A12）e1＋A12d1（e1），

对上式两边左乘e2且由e2f1（A12）e1＝0可得

e2f1（A12）＝0．

又因为

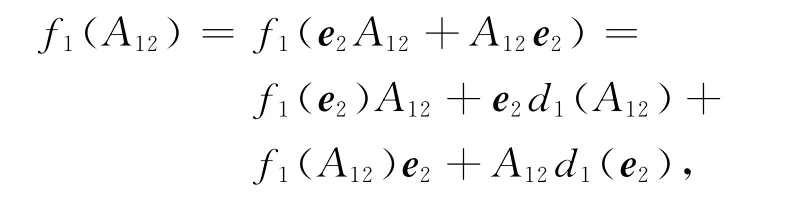
对上式两边右乘e1可得f1（A12）e1＝0．因此，f1（A12）＝f1（A12）e2∈U12．

对于任意的A11∈U11，由引理1（ⅱ）可得

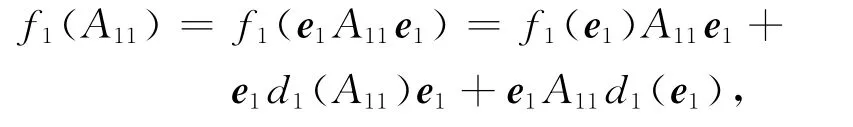
因而，f1（A11）∈U11＋U12．同理可以证明f1（A22）∈U22＋U12．

定理1 设U＝Tri（A，M，B）是三角代数，则U上的每个广义高阶Jordan导子是广义高阶导子．

证明 设F＝ （fi）i∈N是广义高阶Jordan导子，用数学归纳法证明结论．

由引理2可知：当k＝1时，广义Jordan导子是广义导子；而引理3又说明，当k＝1时，对于i＝1，2，满足：

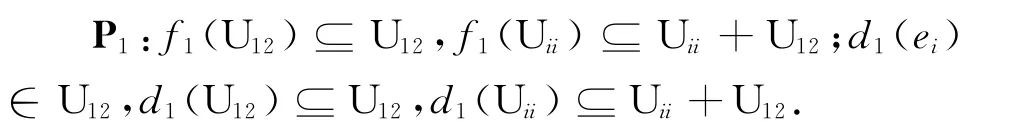
下面设对任意的A、B∈U和任意的k＝s＜n∈N，有fs（AB（B）并且对于i＝1，2满足：

Ps：fs（U12）⊆U12，fs（Uii）⊆Uii＋U12；ds（ei）∈U12，ds（U12）⊆U12，ds（Uii）⊆Uii＋U12．

为了证明当k＝n时结论成立，分为以下4个命题来证明：

命题1 dn（e1）∈U12，dn（e2）∈U12，dn（U12）⊆U12和dn（Uii）⊆Uii＋U12（i＝1，2）．

因为dn（e1）则由Ps可得e1dn（e1）e1＝e2dn（e1）e2＝0．于是dn（e1）∈U12．显然ds（I）＝0，易证dn（I）＝0．因 而，dn（e2）＝－dn（e1）∈U12．

设A12∈U12，则有和

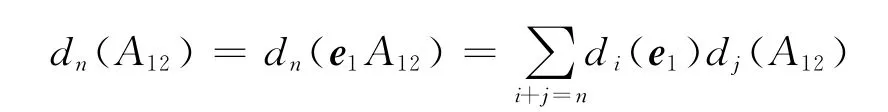
由Ps及dn（e1）∈U12，dn（e2）∈U12可知

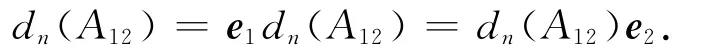
因此，dn（A12）＝e1dn（A12）e2∈U12．

对于任意的A11∈U11，A22∈U22，因为ds（A11）∈U11＋U12，ds（e1）∈U12，则有

因而dn（A11）∈U11＋U12．类似可以证明d2（A22）∈U22＋U12．

命题2 fn（U12）⊆U12，fn（Uii）⊆Uii＋U12（i＝1，2）．

由fn的定义及Ps，显然有

所以有fn（e1）∈U11＋U12，fn（e2）∈U22＋U12．

对于任意的A12∈U12，由引理1（ⅰ）及A12e1＝0可得

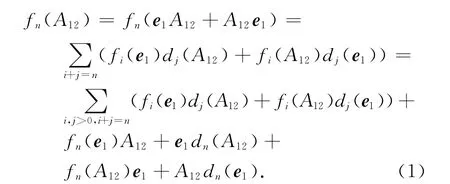
对（1）式两边左乘e2且由e2fn（A12）e1＝0知e2fn（A12）＝0．又因为e2A12＝0，则

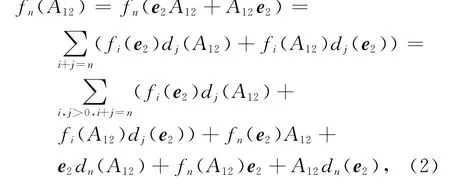
对（2）式两边右乘e1，可得fn（A12）e1＝0．因此，fn（A12）＝e1fn（A12）e2∈U12．

对于任意的A11∈U11，由引理1（ⅱ）可知

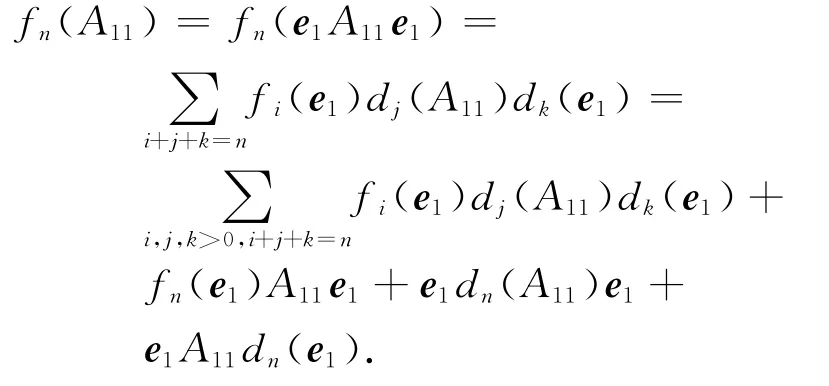
所以有fn（A11）∈U11＋U12．同理可以证明fn（A22）∈U22＋U12．

命题3 （ⅰ）对于任意的A11∈U11，B12∈U12，有fn（A11B12

（ⅱ）对于任意的A12∈U12，B22∈U22，有

（ⅲ）对于任意的Akk、Bkk∈Ukk（k＝1，2），有

对于任意的A11∈U11和B12∈U12，由引理1（ⅰ），命题1、2及Ps可得

类似地可以证明（ⅱ）．

对于任意的A11∈U11，由引理1（ⅱ）及dn是高阶导子，从而有

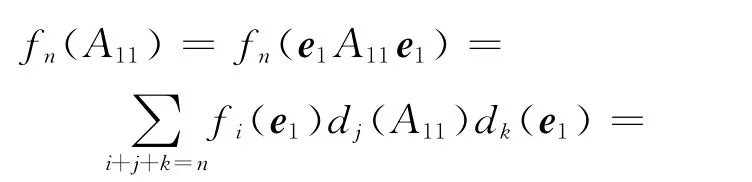
因此，对于任意的A11、B11∈U11，有

由（3）式可得

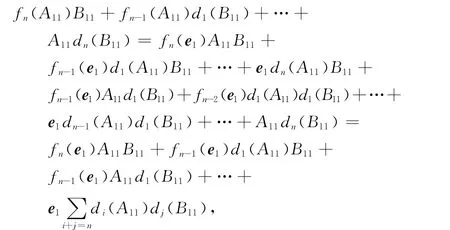
因而可得

类似可以证明

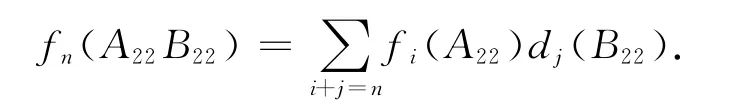
命题4 对于任意的A、B∈U，有

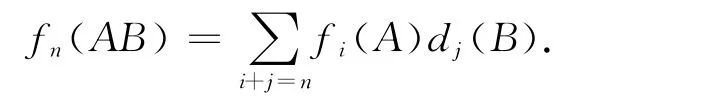
对于任意的A、B∈U，有A＝A11＋A12＋A22，B＝B11＋B12＋B22，其中Aij、Bij∈Uij（1≤i≤j≤2），由命题3可得

再由Ps及命题1、2可知

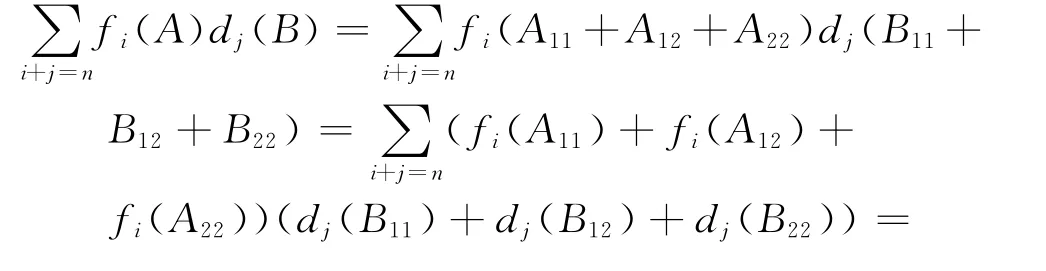
由（3）式可得

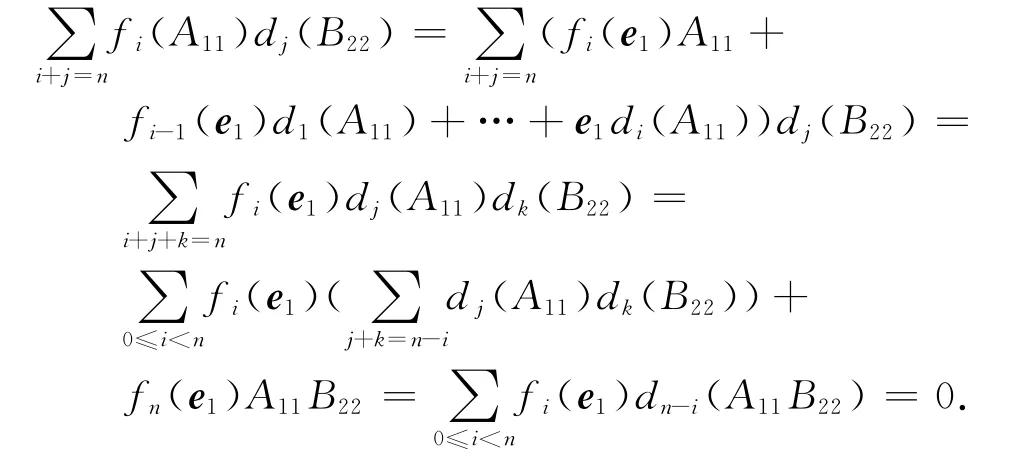
于是fn（AB）即k＝n时结论成立．

综上可知，三角代数上的每个广义高阶Jordan导子是广义高阶Jordan导子．

通过定理1的证明过程可知：对于任意的i∈N，有di（I）＝0．因而一个广义高阶Jordan三重导子是广义高阶Jordan导子．因此，由定理1可得

定理2 设U＝Tri（A，M，B）是三角代数，则U上的每个广义高阶Jordan三重导子是广义高阶导子．

特别地，若对于任意的i∈N，满足fi＝di，则有

推论1 设U＝Tri（A，M，B）是三角代数，则U上的每个高阶Jordan导子是高阶导子．

推论2 设U＝Tri（A，M，B）是三角代数，则U上的每个高阶Jordan三重导子是广义高阶导子．

本文在三角代数上研究了广义高阶Jordan导子和广义高阶Jordan三重导子，证明了在三角代数上，广义高阶Jordan导子、广义高阶Jordan三重导子和广义高阶导子是等价的．我们的结论更具有一般性，如文献［2，4－5，10，15］等的结论均可看成是本文结论的某种特殊情形．

［1］Ma Fei，Ji Guoxing．Generalized Jordan derivation on triangular matrix algebra［J］．Linear and Multilinear Algebra，2007，55（4）：355－363．

［2］Herstein I N．Jordan derivation on prime rings［J］．Proceedings of American Mathmatical Society，1957，8（6）：1104－1110．

［3］张建华．套代数上的Jordan导子［J］．数学学报，1998，41（1）：205－212．

［4］Zhang Jianhua，Yu Weiyan．Jordan derivation on triangular algebras［J］．Linear Algebra and its Applications，2006，419（1）：251－255．

［5］Hou Jinchuan，Qi Xiaofei．Generalized Jordan derivation on nest algebras［J］．Linear Algebra and its Applications，2009，430（5／6）：1479－1485．

［6］朱军，熊昌萍．环上的广义导子与Von Neumann代数上的P－核值保持映射［J］．数学学报，1998，41（4）：795－800．

［7］Dominik BenkoviĉNejc Sirovnik．Jordan derivations of unital algebras with idempotent［J］．Linear Algebra and its Applications，2012，437（9）：2271－2284．

［8］Yan Dangui，Zhang Chengchang．Generalized derivations and bilocal Jordan derivations of nest algebras［J］．Linear Algebra and its Applications，2010，432（3）：2615－2622．

［9］Miguel Ferrero，Claus Haetinger．Higher derivations of semiprime rings［J］．Communications in Algebra，2002，30（5）：2321－2333．

［10］Xiao Zhankui，Wei Feng．Jordan higher derivations on triangular algebras［J］．Linear Algebra and its Applications，2010，432（10）：2615－2622．

［11］Dominik Benkovic，Daniel Eremita．Multiplicative Lie n－derivations of triangular rings［J］．Linear Algebra and its Applications，2012，436（11）：4223－4240．

［12］Cheung Waishun．Commuting maps of triangular algebras［J］．Journal of London Mathematical Society，2001，63（1）：117－127．

［13］Cheung Waishun．Lie derivation of triangular algebras［J］．Linear Algebra and its Applications，2003，51（3）：299－310．

［14］Chen Lin，Zhang Jianhua．Nonlinear Lie derivation on upper triangular matrix algebras［J］．Linear and Multilinear Algebra，2008，56（6）：725－730．

［15］余维艳，邢福弟．三角代数上的广义Jordan导子［J］．数学进展，2009，38（4）：477－480．