Hyperion高光谱影像的经验模态分解及其几个问题的探讨

周子勇

（油气资源与探测国家重点实验室 中国石油大学 地球科学学院，北京 102200）

0 前言

高光谱遥感技术近年发展迅速，并形成了一系列数据处理与信息提取方法，这些方法主要可以归为三类：①继承并发展多光谱遥感影像处理方法，如通过波段比值、PCA分析提取信息；②针对高光谱影像数据特点发展起来的一系列方法，如MNF（Minimum Noise Fraction）、SAM（Spectral Angle Mapper）、SAI（Spectral Absorption Index）、SFF（Spectral Feature Fitting）、MTMF（Mixture－Tuned Matched Filtering）、混合像元解混技术等；③借鉴信号处理领域的新方法对影像进行处理和信息提取，如小波分析方法、分形分析方法、神经网络方法等。

Hilbert－Huang（HHT）变换方法是1998年由Huang［3］首先提出来的一种信号处理方法，用于现实中非线性、非平稳信号的处理与分析。HHT分析方法的前提是经验模态分解。所谓经验模态分解就是通过一种特定的滤波方法把原始数据分解成由高频（细节成份）到低频（基本成份）的一系列本征模态函数。由于不同的本征模态函数分别刻划了原始信号中不同目标的信号成份，因此借助于EMD分析，有可能从遥感影像中分离出不同目标对应的信号成份，进而提取出有用信息。把EMD方法用于遥感影像的分析处理，目前的研究多是对单一图像进行分析。如通过对影像的二维EMD分解（BEMD），提取影像的边界信息［13］、纹理特征［10，12］或者通过 EMD 进行图像融合［1］，或者通过EMD分析不同信号成份的空间分布规律［4］等。这种单波段影像的EMD分析，没有发挥高光谱影像具有丰富的光谱信息的优势。因此作者提出基于像元高光谱曲线进行经验模态分解，构建IMF影像，并对数据特征进行分析。

作者在本文以Hyperion高光谱影像为试验数据，对每一像元的高光谱曲线进行经验模态分解，形成一系列IMF影像，通过分析IMF影像的特点，探讨运用EMD方法进行高光谱影像处理与信息提取的可能性。作者首先简述EMD算法的基本原理，然后对比分析不同IMF影像的特点，最后讨论影响高光谱影像经验模态分解的主要因素以及可能的解决办法。

1 遥感影像的经验模态分解

1.1 经验模态分解算法

经验模态分解算法的基本思想是，通过连续去除原始信号的本征信号要素IMF，从而达到信号分解的目的。其基本算法如下［3］：

给定一信号x（t），对信号x（t）按下列步骤进行处理：

（1）找出信号x（t）的所有极大值点Maxi（i＝1，2，…）和极小值点Mink（k＝1，2，…）。

（2）根据极大值点和极小值点进行三次样条插值，分别得到信号的上包络线Max（t）和下包络线 Min（t）。

（3）计算每一点上包络线和下包络线的平均值e（t），即e（t）＝ （Max（t）＋Min（t））／2。

（4）从信号中减去e（t），即：x（t）＝ x（t）－e（t）。

（5）转回到步骤（1），当x（t）不变化时，停止。这时所得到的x（t）称为第一个IMF，记为IMF1。

（6）从原始信号移去IMF1，即x（t）＝x（t）－IMF1，然后把相减后的结果作为输入数据重复步骤（1）至步骤（5）流程，可以得到IMF2、IMF3…。

（7）当最终分解的IMF没有极值点时（单调上升或下降），停止EMD过程。

从上述算法原理可知，经验模态分解的实质是把原始信号分解成一系列调幅／调频（AM／FM）信号之和，即每一个IMF都是一个AM／FM信号。与傅立叶变换和小波变换相比，经验模态分解所得到的信号，更加直观，易于分析。然而，该方法毕竟是经验分析方法，在实际操作过程中还存在很多的问题，信号的分解受多个因素的影响，后面将对这个问题进行详细讨论。

1.2 高光谱遥感影像的经验模态分解与结果分析

1.2.1 数据来源与处理方法

本文实验数据为2006年获得的一景渤海湾地区的Hyperion影像数据。数据覆盖区大部分为海域，作者截取了其中位于盘锦市附近的近海区域作为研究对象，地面覆盖类型主要为水体、植被及裸露地表。Hyperion数据扫描带宽度为7.5km，空间分辨率为30m，光谱分辨率约为10nm，覆盖400nm～2 500nm的波长范围，共有220个定标的波段。其中有波长重复波段以及噪声特别大没有有效信息的波段，去除这些波段后保留176个波段。表1为保留波段与原始波段对照表。本文中所指的波段号都是指176个波段的编号。

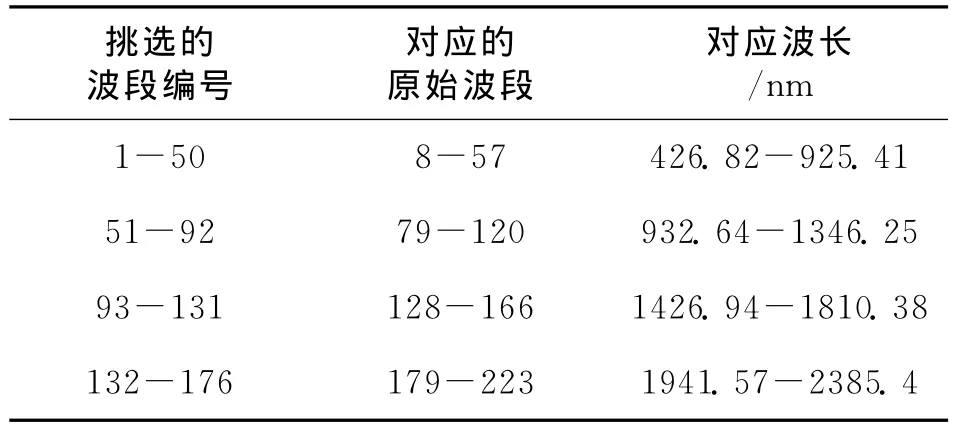
表1 保留波段与原始波段对照表Tab.1 Selected wavebands versus original wavebands

在进行EMD处理前，需要对影像进行预处理。由于作者主要目的是研究原始高光谱影像的经验模态分解效果，因此只对原始数据进行简单的预处理，即把影像的DN值转换为绝对辐射值。转换方法很简单，即把所有VNIR波段（1号～50号）除以“40”，所有SWIR波段（51号～176号）除以“80”，得到绝对辐射值。然后以绝对辐射值进行EMD处理。EMD处理以像元为基础。由于每一像元都对应有一条高光谱曲线，因此可以按照类似于一维时间序列EMD分解方法进行高光谱曲线的分解，并分解得到一系列的IMF。对影像中的每一个像元都进行EMD处理，得到对应的IMF，然后把每一像元同一层次的IMF构成IMF影像，得到IMF1、IMF2等一系列影像。由于不同地物像元高光谱曲线特征不同，分解得到的IMF数目也不一样，实验中首先对不同地物像元高光谱曲线进行经验模态分解试验，分析其IMF特征。结果表明，每一像元可以分解的IMF个数在6个～7个之间。因此在对整个数据进行处理时，把每个像元的IMF个数设定为“8”，这样既便于对不同像元的IMF进行对比，同时又尽可能减少计算量。整个计算过程通过ENVI／IDL编程实现。

1.2.2 结果分析

通过经验模态分解，可以得到一系列IMF影像，每一像元都有一系列的IMF曲线，同时每一个IMF也有一个对应的影像。这样既可以分析每一个像元中每一个IMF的信号特征，又可以分析每一个IMF影像的空间特征。因此与原始高光谱影像数据相比，通过对不同IMF的对比分析，有可能突出更多的细节特征，得到一些其它信号分析方法无法得到的信息。下面通过对Hyperion经验模态分解结果的分析，来说明这一问题。

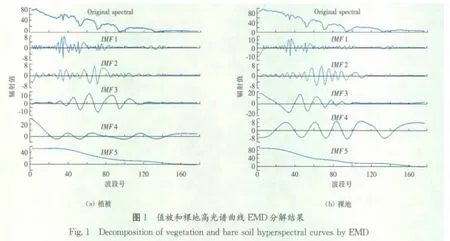
（1）光谱曲线的IMF特征。通过经验模态分解，把光谱曲线分解成一系列由高频到低频的IMF。不同层次的IMF反映了信号中不同的成份，或者说不同的信号来源，因此不同地物的高光谱曲线分解后的IMF也不同。图1是影像中特定像元光谱曲线经验模态分解结果。在图1中，IMF1反映了高光谱曲线的高频特征，而IMF5则反映了曲线的总体趋势。尽管从图1上看，两种地物其原始波谱曲线差异并不明显，但分解的IMF差异却相当明显。根据IMF的特征差异，可以用于影像分类［11］。

（2）通过IMF分析影像的噪声特征。一般来说，IMF1对应是光谱曲线的高频成份，反映信号中的噪声或细节成份。因此通过分析IMF1，可以了解高光谱影像中每一波段的噪声水平和性质。为了评价各波段的噪声水平，分别计算出了每一波段原始影像及对应IMF1影像的方差，并通过其比值来评价原始影像的噪声特征。如图2所示为每一波段原始影像、对应的IMF1影像的方差及其比值。由图2可知，在不同波段其比值大小表现出不同的特征。在28号～57号（对应的波长范围为：701.55nm～993.17nm，下 同 ），1 号 ～3 号（426.82nm ～ 447.17nm），70 号 ～ 71 号（1 124.28nm ～1 134.28nm），93 号 ～98 号（1 426.94nm～1 477.43nm），131 号 ～132 号（1 810.38nm～1 941.57nm），138 号 ～139 号（2 002.06nm～2 012.15nm）波段区间，其比值相对较小，其它波段区间比值相对较高。

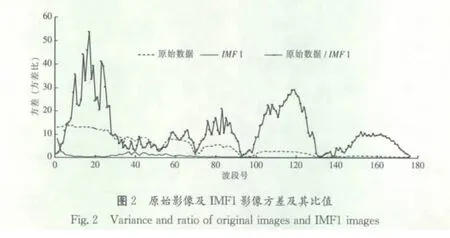
由于IMF1反映信号中的噪声或细节成份，因此该比值大小在某种程度上反映了各波段噪声的性质。比值较大的波段，IMF1反映的主要是影像中的系统噪声；而比值较小的波段，既有可能是原始影像的信噪比较低，也有可能是IMF1反映了影像的细节。这点通过对比图3和图4可以看得很清楚。图3为第16波段原始影像及其对应的IMF1影像，图4为138波段原始影像及其对应的IMF1影像。显然在图3中，IMF1反映的是系统噪声，而图4中的IMF1则反映了原始信号中较强的背景噪声，由于背景噪声大，原始影像中目标信息被掩盖，而在IMF1中，目标信息被突出了。因此通过对比原始影像及对应的IMF1影像，不但可以知道每一波段的噪声大小，而且还可以了解噪声的性质。

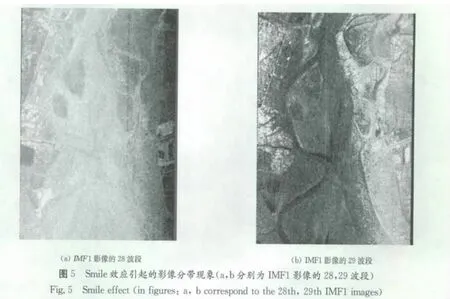
（3）Smile效应。未经处理的高光谱影像存在Smile效应。如果影像存在Smile效应，则通过MNF处理后的影像，其灰度在空间上有明显的线性分带特征。这种特征在IMF中也可以表现得非常明显。如图5所示分别为IMF1的28号和29号波段影像，由图5可见明显的灰度空间分带现象。

（4）与小波分析或FFT分析不同，经验模态分解后的结果，与原始信号的波段存在一一对应关系，因此原始影像和IMF影像，对比更直观，解释更容易。

3 EMD中几个问题的探讨

影响高光谱影像经验模态分解结果的因素很多，其中影响最大的因素主要有以下四个方面：①极值点的位置和极值的确定；②插值算法；③端点效应；④IMF终止条件。下面对上述影响因素进行讨论。

3.1 极值点的位置和极值的确定

确定极值点的位置和极值的大小是经验模态分解的基础。寻找原始信号的极值点，可以采用下述算法：

极大值点 Maxi：If （xi≥xi－1and xi＞xi＋1）or （xi＞xi－1and xi≥xi＋1）

极小值点 Mink：If （xi＜xi－1and xi≤xi＋1）or （xi≤xi－1and xi＜xi＋1）

这种算法计算简单，但是由于只是简单的比较相邻值，因此原始数据中的噪声有可能产生一些不必要的极值点。特别是对于遥感影像，除系统本身的误差外，还受大气、下垫面等因素的影响，噪声来源较多。而且在做EMD分解前，只是把DN值转换成了辐射绝对值，并未做去噪处理，因此因噪声产生的极值点不可避免，在进行EMD处理时，应该去除这类极值点。为了解决这一问题，在确定极值点时，先计算相邻两极值点的极差，然后设定一阈值，把极差小于阈值的极值点去除。也有文献［6］提出通过相邻三个极值点插值的方法来解决。这种方法的有效性有待于进一步验证，而且计算量大，特别是对于本文的大数据量，计算量会增加很多，为此作者采用简单的相邻值比较方法。

3.2 插值算法

插值是EMD的一个重要组成部分。Huang［3］提出采用三次样条方法进行插值，根据极小值和极大值求得最大最小包络线。由于不同插值方法得到的最大最小包络线可能不完全一样，因此分解的IMF也可能存在一定的差异。许多文献讨论了插值方法对EMD结果的影响［5，9］，如何根据实际数据选择最优插值方法，目前并没有更多的研究和判别标准，而且也没有一种普适的算法。但目前大多数的文献都采用三次样条方法来处理不同的数据，因此作者仍然采用三次样条方法。

3.3 分解结束判别标准

EMD整个过程涉及两个停止条件，①IMF的判别条件；②整个分解过程的结束条件。对于前者，Huang给出了两个条件：一是IMF 中极值点的数目与曲线穿越零值点的个数相等或相差1个；二是IMF的上包络线和下包络线各点的平均值为零。显然，第一个条件包含在第二个条件中。所以确定IMF的关键是如何给出第二个条件，由于实际计算中第二个条件很难精确确定，Huang建议通过前后两次计算的均方差来判断IMF的合理性，但这种方法有时难以达到好的效果［2］。

对于EMD的结束条件，可以根据最终分解的结果是否为单调曲线来确定。但是这一判别条件，有可能出现IMF冗余现象，即分解的IMF比实际的要多，从而不能反映信号的真实成份。为此，有文献提出采用能量变化作为判别准则。无论哪种方法，都只是针对单一信号曲线而言。对于高光谱影像，由于需要对每一个像元的高光谱曲线进行一维经验模态分解，并最终形成IMF影像，因此必须保证每一个像元对应高光谱曲线分解后的IMF具有可比性。为了解决多信号IMF可比性问题，Rato提出通过一个所谓的分辨率因子的办法，文中所说的分辨率因子，指的是上下包络线平均值的能量与原始信号能量的比值。显然分辨率因子值越小，分解的IMF个数越少；反之越大。因此通过调整每一个信号分解过程中的分辨率因子，就可以保证各信号分解的IMF个数相同，使相同级的IMF具有可比性。但文中并没有具体给出分辨率因子的确定方法。实际上，当对未知信号进行分解时，分辨率因子的选择本身就存着在判别标准的问题。

还有一种简单的方法，就是把IMF的个数设定为一常数。当大致知道分解的IMF个数时，可通过这种方法简单设定，而且也便于对比。通过对试验数据进行经验模态分解，发现每一像元的高光谱曲线分解的IMF个数都是“6”或“7”，基于上述考虑，作者把IMF分解个数设定为“8”，经计算结果表明，此结束判别条件不会对结果产生太大的影响。

3.4 端点效应

高光谱曲线的两个端点一般都不是极值点，对曲线两个端点的处理，会对分解的IMF产生影响，即端点效应问题。很多文献讨论了减少端点效应的解决办法。常用方法主要有以下几种：①依据端点与邻近值的关系直接指定极值点，即如果与端点相邻点为极小值点，则把该端点作为极大值；否则作为极小值。该方法简单，但误差较大；②根据与端点相邻的两个极值点向相反方向延展极值点［6］。基本的思路如下：设信号第一个极大值和极小值分别为Max1、Min1，其对应的位置分别为tmax1和tmin1，则在－tmin1处插入极大值 Max1，在－tmax1处插入极小值Min1，按同样的方法在信号末端拓展两个极值，然后进行插值处理；③与第二种类似，只是采用更多的极值（总极值数的一半）进行拓展［8］；④分别以信号首端和尾端为对称点把原始数据进行镜像取值，形成一个三倍于原始数据的数据量，插值完成后，截取中间部分进行计算。除此之外，还有一些其它方法，但是这些方法都是基于实际数据的比较，并没有一个判别标准。对于高光谱曲线，也可以采用上述方法消除端点效应。本文作者分别试验了上述四种方法，结果认为第二种方法效果较好。

4 结论

作者在本文采用EMD方法对Hyperion影像进行处理，并对结果进行了初步分析。实验结果表明，通过分析IMF，可以更好地描述遥感影像，了解影像的固有特征，因而可以基于IMF进行特征提取。但是，由于EMD方法本身存在不足，在基于EMD的高光谱影像处理时，还存在许多问题有待于进一步研究。另外对于大量的高光谱数据，其计算量也是一个必须考虑的问题。尽管如此，EMD方法还是有它的独特之处，特别是经验模态分解结果，与原始数据可比性好，与其它分析（如小波分析、分形分析）相比，结果更直观，因此有值得进一步研究的必要。作者只是初步讨论了运用EMD分解来了解Hyperion影像的特征，下一步将综合高光谱影像的一维和二维经验模态分解结果，研究不同地物与IMF的对应关系，以及基于IMF的高光谱影像特征提取方法。

［1］CHEN SHAOHUI，SU HONGBO，ZHANG RENHUA，et al.Fusing remote sensing images using atrous wavelet transform and empirical mode decomposition［J］.Pattern Recognition Letters.2008，29：330－342.

［2］CHENG J S，YU D J，YANG Y.Research on intrinsic mode function（IMF ）criterion in EMD method［J］.Mechanical Systems and Signal Processing，2006，20：817－824.

［3］HUANG N E，SHEN Z，LONG S R，et al.The em－pirical mode decomposition and Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proceedings of the Royal Society of London A.1998，454：903－995.

［4］NUNES J C，BOUAOUNE Y，DELECHELLE E.Image analysis by bidimensional empirical mode decomposition［J］.Image and Vision Computing，2003，21，12：1019－1026.

［5］QIN S R，ZHONG Y M.A new envelope algorithm of Hilbert Huang transform［J］.Mechanical Systems and Signal Processing，2006，20：1941－1952.

［6］RATO R T，ORTOGIEORA M D，BATISTA A G.On the HHT，its problems，and some solutions［J］.Mechanical Systems and Signal Processing.2008，22：1374－1394.

［7］RILLING G，FLANDRIN P.On the influence of sampling on the empirical mode decomposition，in：Proceedings of the International Conference on A－coustics［J］.Speech and Signal Processing，ICASSP 2006：III－444－III－447.

［8］RILLING G，FLANDRIN P，GONcALVES P.On empirical mode decomposition and its algorithms，in：IEEE－EURASIP Workshop on Nonlinear Signal and Image Processing NSIP－03，Grado［C］.2003.

［9］XU Z G，HUANG B X，LI K W.An alternative envelope approach for empirical mode decomposition［J］.Digital Signal Processing，2010，20：77－84.

［10］ZHANG Y，SUN Z X，LI W H.Texture synthesis based on Direction Empirical Mode Decomposition［J］.Computers ＆ Graphics，2008，32：75－86.

［11］董士伟，周子勇，基于EMD与神经网络的油膜高光谱数据特征提取［J］.遥感技术与应用，2010，25（2）：221－226.Dong Shiwei，Zhou Ziyong，Wen Baihong.Feature Extraction of Offshore Oil Slick from Hyperspectral Data Based on EMD and Neural Network［J］.Remote sensing technology and application，2010，25（2）：221－226.

［12］沈滨，崔峰，彭思龙.二维EMD的纹理分析及图像瞬时频率估计［J］.计算机辅助设计与图形学学报，2005，17（10）：2345－2352.Shen Bin，Cui Feng，Peng Silong.Bidimensional EMD for Texture Analysis and Estimation of the Instantaneous Frequencies of an Image［J］.Journal of computer2aided design ＆computer graphics，2005，17（10）：2345－2352.

［13］万建，任龙涛，赵春晖，二维EMD应用在图像边缘特征提取中的仿真研究［J］.系统仿真学报，2009，21（3）：799－822.Wan Jian，Ren Longtao，Zhao Chunhui.Simulation Research of Applying Two－dimensional Empirical Mode Decomposition on Image Feature Extraction［J］.Journal of System Simulation，2009，21（3）：799－822.