各向异性碳酸盐岩储层精细横波速度估算方法

王保丽，印兴耀，吴志华，2

（1.中国石油大学 地球科学与技术学院，山东 青岛 266580；2.中国石化股份胜利油田分公司 地质科学研究院，山东 东营 257015）

0 前言

弹性波正演模拟及叠前地震反演都离不开横波速度测井资料，但在实际生产中，由于成本因素及横波测井技术尚不成熟，横波测井资料比较缺乏。为获得准确的横波资料，国内，外专家学者主要从经验公式和岩石物理两个方面对横波速度估算进行了研究。Castagna、Han、Jorstad［1－3］等人通过经验公式拟合得出纵波和横波速度的关系式；李庆忠院士［4］给出了具有普遍适应性的抛物线拟合公式，奠定了由纵波估算横波的基础。尽管以上经验公式拟合方法具有比较容易实现的优点，但其精度不能保证，在实际应用中需要对拟合横波进行进一步的修正才能得到与储层比较吻合的横波速度。相对于经验公式拟合方法的不足，借助岩石物理理论模型的横波速度估算方法更具优势。王玉梅［5］等人借助岩石物理模型进行了横波速度的计算，获得了与实测横波吻合度较高的预测结果，云美厚［6］等人利用Biot－Gassmann方程得到了砂岩的横波速度理论计算方法；郭栋［7］等人在测井、地震资料约束下对Xu和White联合K－T模型、微分等效介质理论及Gassmann理论提出的碎屑岩理论模型（Xu－White模型［8］）的应用进行了研究，取得了较好的横波速度预测结果。基于岩石物理的横波速度估算方法物理意义明确，计算精度高，但目前的研究仍有较大的局限性。比如，应用比较广泛的Xu－White模型仅方便了人们对碎屑岩储层横波速度的估算。随着目前勘探重心往碳酸盐岩和各向异性储层的转移，准确、有效地估算碳酸盐岩和各向异性储层的横波速度方法是十分必要的。为满足现代勘探开发的需求，作者首先基于碳酸盐岩、各向异性储层等不同类型的储层物性的不同，在岩石物理理论分析的基础上，建立了各向异性碳酸盐岩储层的岩石物理理论模型；其次，提出了针对各向异性碳酸盐岩储层的横波速度精细估算方法；最后，利用提出的方法进行了实际资料的横波速度估算，将估算横波与实测横波进行了对比分析。结果表明，该估算方法可成功模拟各向异性碳酸盐岩储层的横波速度，研究成果在实际工区得到成功应用，显示出良好的应用前景。

1 横波速度估算的基本流程

为说明横波速度估算的基本流程，现以经典的Xu－White模型［8］为例，对碎屑岩储层的横波速度估算方法进行描述。

1.1 储层岩石等效弹性模量的求取

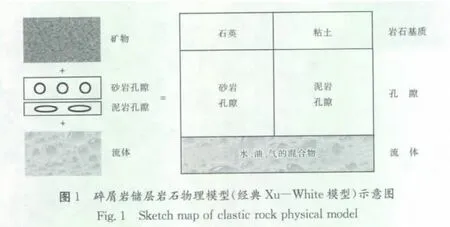
Xu－White模型通过引入孔隙纵横比，假定岩石总孔隙空间由砂岩粒间孔隙和粘土粒间孔隙（包含束缚水）组成。该模型的主要特征是两种孔隙空间的几何形状有较大差异，而且对弹性模量的影响也不同。模型示意图如图1所示。

在假定干岩石骨架泊松比不随孔隙度变化的情况下，首先将计算干岩石骨架弹性模量的Kuster－Toksöz方程［9］简化为：

然后，利用wood方程将孔隙流体进行混合，计算混合流体的体积模量Kf：

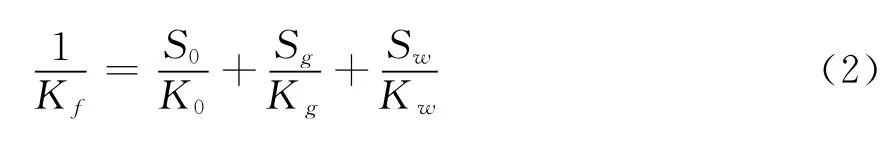
式中 K0、Kg和Kw分别是油、气和水的体积模量；S0、Sg和Sw分别是油、气和水的饱和度，且有S0＋Sg＋Sw＝1。

最后，利用Gassmann方程（方程（3））计算饱含流体岩石的体变模量和剪切模量：

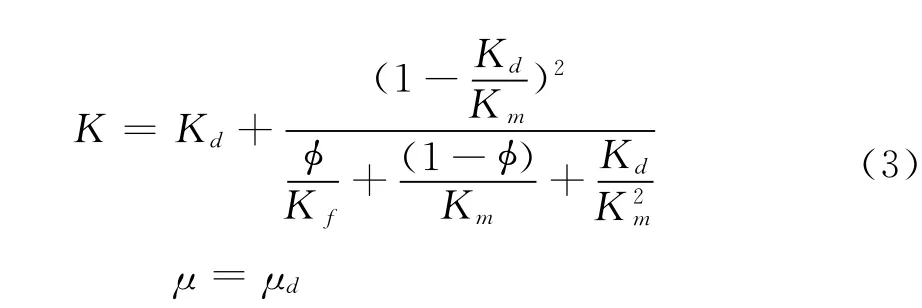
式中 K和μ分别是饱含流体岩石的体积模量和剪切模量；Kf是孔隙流体的体积模量。

1.2 基于模型与测井曲线的横波速度估算

为获得合适的模量参数信息，使估算的横波速度具有一定的准确性，还需充分考虑岩石基质、泥质含量、孔隙流体、孔隙大小、孔隙形状等岩石物理参数。

由于方程（1）、方程（2）中所涉及的骨架和流体都是单组份的岩石，因此可把方程中岩石基质及流体的模量值看作是多种组份的等效模量。因此，在实际计算中，首先要通过对岩石组份的分析，确定其孔隙形状和矿物胶结状态，然后根据其特点选取相匹配的等效介质、自适应理论或颗粒接触理论等不同的模型，最后借助其中的Voigt－Reuss－Hill平均、Kuster－Toksöz公式、Walton模型等岩石物理理论［10］来计算流体矿物模量。

泥质含量和孔隙度通常由测井资料来获取，若不易直接获取，需要借助孔隙度、速度、泥质含量、密度等岩石物理参数间的关系，由密度、速度、自然伽玛、电阻率和中子测井等常规测井曲线间接计算得到。

借助与储层相匹配的岩石物理理论模型和所需的常规测井资料，再利用方程（1）、方程（2）和方程（3）便可获得岩石的等效模量参数，最终由下式可以计算得到饱含流体岩石的纵波、横波速度VP、VS。

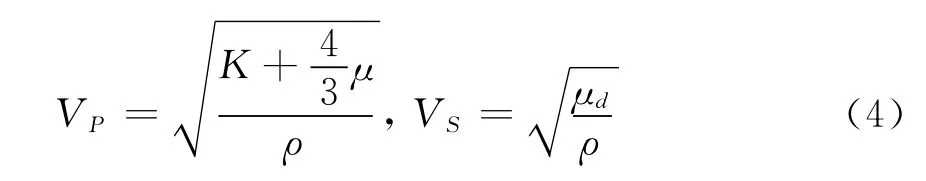
1.3 井震联合约束下的横波速度修正

在实际应用中，由于岩石基质模量、密度等参数通常不易直接获取；实际参数因地而异，经验参数的单一应用也会引入较大的计算误差。因此，为使估算横波更接近实际，消除横波速度估算的不确定性，还需要通过井震联合约束反演对前一步估算结果进行修正。

测井约束反演的基本原理是以较为精确的声波和密度曲线作为控制曲线，利用理论模型及经验公式，通过重构密度和纵波速度，构建其输入和输出参数之间的关系，建立反演格式，通过非线性反演［11］求取估算横波速度所需的密度和岩石模量信息。

首先，对于砂、泥及流体的密度，可利用Wood加权平均公式（方程（5））来重建密度曲线：

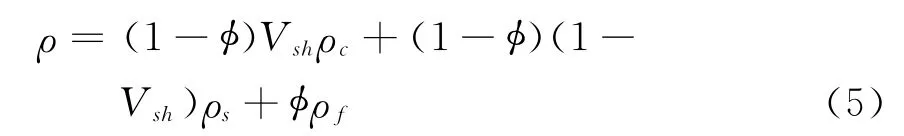
其中 φ为孔隙度；Vsh为岩石的泥质含量；ρ为岩石的总密度，ρs、ρc、ρf分别为砂、泥及流体的密度。按不同的时间间隔段，分别代入下面的反演目标函数J（x）：

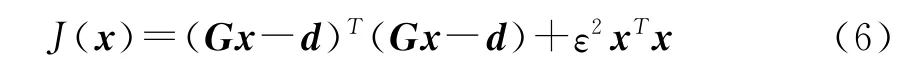
其中 x＝［ρsρcρf］T；d是由时间间隔段内各采样点处的密度值组成的向量，G是由各采样点处的孔隙度φ和泥质含量Vsh组成的系数矩阵；ε2为加权因子，或称阻尼系数。

同理，将干岩骨架及岩石基质体变模量代入方程（3），将饱含流体岩石体变模量和剪切模量分别表示为与泥质含量、孔隙度、砂、泥岩模量和混合流体模量有关的函数，通过重建纵波速度曲线可反演出的砂、泥岩的剪切模量μm和μsh。

最后，利用反演出的密度ρ和剪切模量μ即可得到初步修正的横波速度。

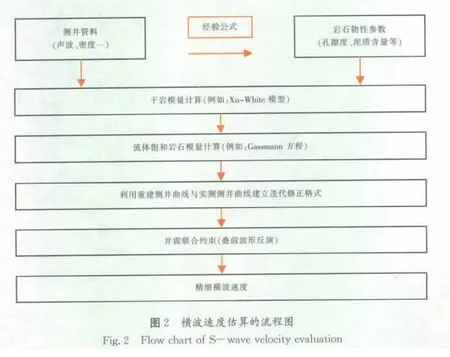
此外，为保证反演解的可靠性，获得与实际储层更加符合的横波速度，可将纵波、初步修正的横波速度和密度作为先验信息，结合实际叠前地震资料进行井震联合约束下的叠前波形反演。本文作者在采用遗传算法，先利用先验信息正演模拟得到叠前合成地震道集，再将合成道集与实际观测的CMP道集进行比较，根据二者的匹配程度能得到最佳描述地下地质情况的纵波、横波速度和密度信息。从而将初步修正的横波速度进行了再次修正，得到了更符合实际地质情况的精细横波速度。综上所述，图2给出了以碎屑岩储层为例的横波估算的流程图。

2 碳酸盐岩储层的横波速度估算

随着勘探开发的深入开展，碳酸盐岩和各向异性储层等复杂油气藏成为了目前勘探的重点。实际研究表明，对碎屑岩进行横波速度估算的Xu－White模型，不能用于碳酸盐岩和各向异性储层的横波估算。只有针对这些储层的特性，构建与之相匹配的岩石物理模型才能获得利于岩性预测的精确横波速度。

2.1 碳酸盐岩储层特性分析

与以粒间孔隙为主的碎屑岩相比，碳酸盐岩的孔隙类型复杂多样［12］，包括：铸模孔隙、溶洞、粒间孔隙、粒内孔隙和裂缝等。孔隙形状是影响碳酸盐岩岩石物理性质，尤其是纵波、横波速度的重要因素［13］，孔隙类型的不同可以导致纵波速度改变40%［14］。因此，在构建理论模型时，必须充分考虑孔隙类型的特点，才能准确估算储层的横波速度。

图3与图4分别给出了孔隙度在0%～30%的范围变化时，不同孔隙类型对岩石速度及模量的影响。由图3及图4可知：①当岩石中充满了溶洞时，速度是最高的，此时岩石最为坚硬；②当岩石中仅有粒间孔隙时，速度比充满溶洞的岩石低而比充满裂缝的岩石高，坚硬程度位于两者中间；③当岩石中仅有裂缝孔隙时，此时岩石最为柔软，速度最低；④当岩石孔隙由溶洞与粒间孔隙两种组成，岩石比第①种情况柔软，比第②种情况坚硬；⑤当岩石孔隙由裂缝与粒间孔隙两种组成，岩石比第③种情况要坚硬，比第②种情况柔软。另外，裂缝对速度及模量的影响最为显著。

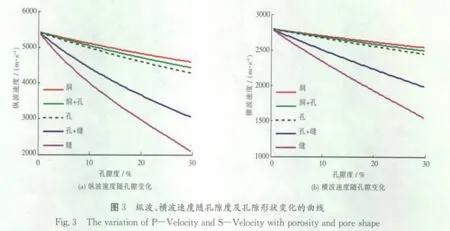
一般情况下，铸模孔隙和溶洞是圆形的，因此，它们能使岩石比孔隙类型为粒间孔隙的岩石坚硬；微孔隙，如微裂缝，能使岩石比孔隙类型为粒间孔隙的岩石柔软。因此，在构建岩石物理模型之前，需要先确定碳酸盐岩储层的孔隙类型及孔隙纵横比参数。

在新授课中，学生是在教师创设的特定情境中探究获取相应的生物学知识，但是所学知识的结构性较差，通常是碎片化的知识，难以在复杂情境中实现有效的迁移。这就需要教师在复习课中引导学生将已学过的碎片化知识进行归纳整理，提炼同化、构建与完善学生的生命观念，加深学生对生命本质的认识。

2.2 岩石物理理论模型的构建

考虑到碳酸盐岩孔隙形状的复杂性，依据Kumar和Han［15］的思想，作者将总孔隙分为四种类型：①孔洞（或称为硬孔隙或球形孔隙，纵横比0.5～1.0）；②粒间孔隙（纵横比0.1～0.5）；③微裂缝（或称为裂缝孔隙，纵横比0.01～0.1）；④泥岩孔隙（束缚水或不连通孔隙）。即：

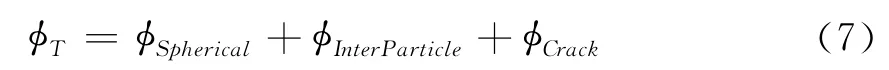
其中 φT为总孔隙度；φSpherical为硬孔隙度；φInterParticle为粒间孔隙度；φCrack为裂缝孔隙度。

在已知储层纵横比速度的情况下，赵克超等［16］人提出了利用KT方程来判断孔隙类型并求取孔隙纵横比的方法，但该方法与本文的情况相反。因此，在上述分类的基础上，本文作者在对不同类型的孔隙分别采用Xu－White模型、微分等效介质（DEM）理论、HS上限、Wyllie时间平均等基础理论模型计算不同类型孔隙的纵横比αSpherical、αInterParticle、αcrack。计算步骤如下：

（1）对于给定的粒间孔隙、溶洞、裂缝，分别利用时间平均方程、HS上限、HS下限来计算纵波速度。

（2）对于给定的孔隙度和初始的纵横比（φInterParticle＝0.1，φSpherical＝1，φCrack＝0.01），利用DEM 理论来计算岩石的纵波速度。VP，DEM＝（Km，μm，α，φ），其中Km和μm是基质的体积和剪切模量。

（3）如果 （VP，DEM（α）－VP（α））2＞ε，则α＝α±δα；反之，则接受每一种孔隙的纵横比。

（4）最后可分别得到粒间孔隙的纵横比αp，溶洞的纵横比αs，裂缝的纵横比αm。

2.3 碳酸盐岩储层的横波估算

计算碳酸盐岩的干岩石模量时，与碎屑岩类似，同样将岩石基质和不同孔隙的体积分量、孔隙纵横比和与之相关的参数代入方程（1）中，对于碳酸盐岩储层，不同之处在于l＝p、s、m、Vp、Vs和Vm分别是粒间孔隙、溶洞和裂缝的体积分量；αp、αs和αm分别是粒间孔隙、溶洞和裂缝的纵横比。

对于碎屑岩储层，常采用Gassmann流体替换方法计算饱含流体时储层的等效弹性模量，但该方法的假设条件是岩石宏观上是均匀分布且含流体岩石完全饱和。由于碳酸盐岩储层孔隙类型的复杂性，其孔隙流体的分布是非均匀的，与Patchy saturation模型描述的“斑块”特征比较吻合，因此，本文作者在假设碳酸盐岩储层孔隙中的流体是呈斑块状分布的，利用Patchy Saturation模型［17］来模拟饱含流体时的等效模量。

首先，利用Gassmann方程分别计算水、油、气饱和情况下，岩石弹性模量Ksat，water、Ksat，oil、Ksat，gas；然后，结合水、油、气各自的饱和度Sw、So、Sg，通过Patchy Saturation模型，来计算流体不均匀分布情况下的碳酸盐岩体积模量Ksat和剪切模量μsat：

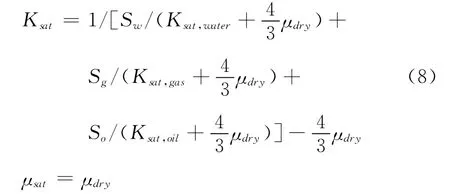
最后，将计算出的等效模量代入方程（4）可初步获得碳酸盐岩储层的纵波、横波速度信息。以此为基础，利用井震联合约束反演对横波速度初步估算结果进行修正，可最终获得精确的横波速度信息。

3 各向异性碳酸盐岩储层的横波速度估算

在碳酸盐岩孔隙系统中，裂缝的存在会引起岩石的各向异性，而各向异性是影响地震AVO现象的重要因素［18－20］，因此，只有充分考虑碳酸盐岩储层的各向异性特征，才能更准确地描述储层的特性。

3.1 岩石物理理论模型的构建

与各向同性储层相比，各向异性储层横波速度估算的关键是含裂缝情况下岩石等效弹性模量的计算。由于各向异性介质的复杂性，作者采用“等效”的思想建立各向异性的等效介质模型，首先将各向异性介质等效为不同的等效介质模型，然后利用等效的介质模型来计算干岩石骨架模量及饱含流体的模量，其等效过程示意图如图6所示。

（1）利用Reuss－Voigt－Hill平均将岩石中的矿物进行混合，得到“岩石基质”模量，然后将含泥质束缚水的“岩石基质”等效为介质“1”，利用Kuster－Toksöz模型将含水的泥质孔隙加入基质中，得到等效介质“1”的模量 K1、μ1。

（2）向等效介质“1”中加入含有混合流体的孔洞和粒间孔隙，获得等效介质“2”，利用微分等效介质和Kuster－Toksöz理论将含混合流体的溶洞和粒间孔隙加入系统，得到等效介质“2”的弹性模量。

（3）基于各向同性碳酸盐岩储层的分析，可将充满流体的粒间孔隙，溶洞和泥岩裂缝与岩石基质等效成为各向同性背景介质，因此，可利用Eshelby－Cheng模型［21－22］计算含裂缝介质的各向异性“干岩石”骨架弹性模量矩阵。

（4）将干岩石骨架的弹性模量代入Brown－Korringa［23］推导的各向异性岩石骨架有效弹性模量与该骨架充填流体时有效模量之间的理论关系式，即Gassmann公式的各向异性形式，计算饱和岩石的弹性参数，该公式用弹性柔性张量来表示，即：

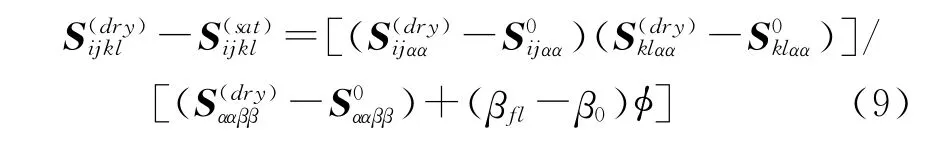
3.2 各向异性碳酸盐岩储层的横波估算

各向异性碳酸盐岩储层的岩石物理模型可用来估算岩石的横波速度、裂缝密度及各向异性参数。储层的横波速度可以通过TTI介质速度公式［24］得到，同时还可以计算HTI介质的各向异性参数ε（V）、γ（V）、δ（V）。由于在模型中用到的 Eshelby－Cheng模型是VTI的，饱和岩石的弹性模量矩阵也是VTI形式的。因此，可以先利用VTI弹性矩阵计算Thomsen各向异性参数ε、γ、δ，再求取HTI介质中的各向异性参数［25］。

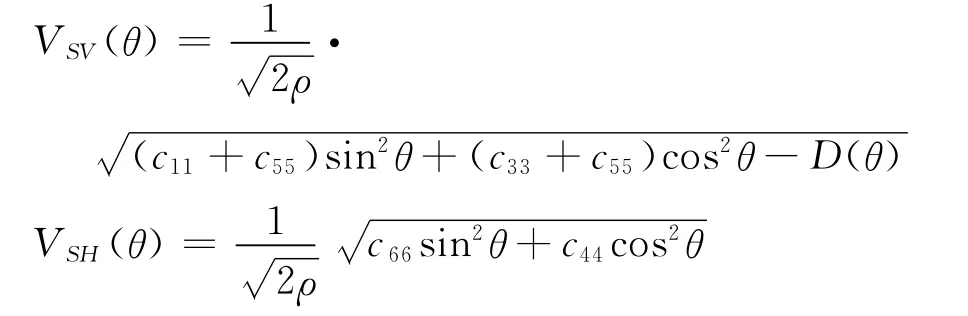
其 中 D（θ） ＝ ｛［（c11－ c55）sin2θ － （c33－c55）cos2θ］＋4（c13＋c55）2sin2θcos2θ｝1／2，c11、c13、c33、c55为弹性模量矩阵中的常数；ρ为介质的密度；VSV为qS波速度；VSH为qSH波速度；θ为波的传播方向与对称轴之间的夹角。

在基于模型的横波估算结果基础上，利用井震联合约束反演对模型估算结果进行修正，进而可以得到更加精确的横波速度。

4 实际资料应用

下面对某碳酸盐岩工区的A井进行横波速度估算，用以检验上述各向同性，即未考虑裂缝影响时的碳酸盐岩理论模型和各向异性碳酸盐岩理论模型以及横波估算方法的准确性。

在实际应用时，需要已知岩石的孔隙度、密度、含水饱和度、方解石含量、白云石含量、泥质含量等参数信息，这些参数需要从实际工区的测井数据得到。还需要已知岩石及流体模量等实验参数，有条件者可通过实验室测量得到，无条件的话可以用经验值代替，只是准确性比实验室测量的差些。另外，描述各向异性岩石的性质不可避免要考虑到角度因素：①方位角，即介质对称轴与观测系统x轴的夹角，假设为“0”；②波传播方向与对称轴的夹角，亦假设为“0”；③介质对称轴与观测系统z轴的夹角，为表示HTI介质，假设为π／2。

图7为对A井数据应用两种模型后得到的横波速度估算结果与实测曲线的对比图，图7（a）为纵波速度曲线，图7（b）为横波速度曲线，其中黑色曲线表示实测结果，蓝色曲线表示各向同性，即未考虑裂缝影响时的碳酸盐岩理论模型的应用效果，红色曲线表示各向异性碳酸盐岩理论模型的应用效果。由于在计算时把纵波速度作为控制曲线，可以看出，图7（a）中三条纵波曲线没有明显差异，图7（b）中，两种模型均可估算得到较为准确的横波速度，但由各向异性的碳酸盐岩岩石物理模型得到的估算结果准确度更高。

5 结论

面对横波速度资料普遍比较缺乏的情况，作者以Xu－White模型为例介绍了储层的横波速度估算方法。在此基础上，构建了各向异性碳酸盐岩储层的岩石物理理论模型，该模型考虑了碳酸盐岩储层复杂的孔隙系统，并对存在裂缝的储层进行了各向异性分析，克服了传统等效介质模型的不足；借助构建的模型给出了各向异性碳酸盐岩储层横波速度的估算方法。最后，实际资料应用结果表明，应用该方法得到的估算横波速度与实测曲线有很好的吻合性，证明了本文方法的准确性和实用性。总之，本文作者在将横波速度的精细估算方法由碎屑岩储层推广到各向异性碳酸盐岩储层，从广义角度来说，该方法还对目前勘探开发研究的热点低孔致密砂岩储层的研究具有一定的指导和借鉴作用。

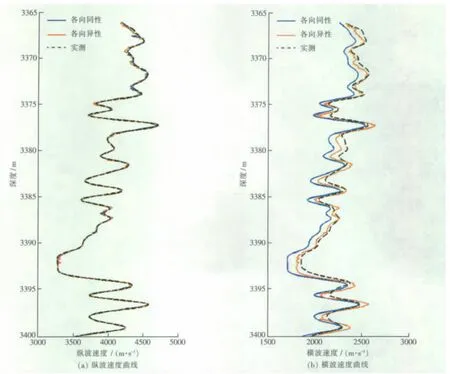
图7 纵波、横波速度估算结果与实测曲线的对比Fig.7 Comparison of evaluated P－wave velocity and S－wave velocity with metrical logs

［1］CASTAGNA J P，BATZLE M L，EASTWOOD R L.Relationships between compressional－wave and shear－wave velocities in clastic silicate rocks［J］.Geophysics，1985，50（4）：571－581.

［2］HAN D H，NUR A，MORGAN D.Effects of porosity and clay content on Wave velocities in sandstones［J］.Geophysics，1986，51（11）：2093－2107.

［3］JORSTAD A，MUKERJI T，MAVKO G.Modelbased shear－wave velocity estimation versus empirical regressions［J］.Geophysical Prospecting，1999，47（5）：785－787.

［4］李庆忠.岩石的纵、横波速度规律［J］.石油地球勘探.1992，27（1）：1－12.

［5］王玉梅，苗永康，孟宪军.岩石物理横波速度曲线计算技术［J］.油气地质与采收率，2006，13（4）：58－61.

［6］云美厚，管志宁.储层条件下砂岩纵波和横波速度的理论计算［J］.石油物探，2002，41（3）：289－292.

［7］郭栋，印兴耀，吴国忱.横波速度计算方法与应用［J］.石油地球物理勘探，2007，42（5）：535－538.

［8］XU S，WHITE R E.A physical model for shearwave velocity prediction［J］.Geophysical Prospecting，1996，44（5）：687－717.

［9］KUSTER G T，TOKSöZM N.Velocity and attenuation of seismic waves in two－phase media［J］.Geophysics，1974，39：587－618.

［10］MAVKO G，MUKERJI T，DVoRKIN J.The Rock Physics Handbook ［M］. Cambridge University Press，1998.

［11］YOUZWISHEN C F.Non－linear sparse and block constraints for seismic inversion problems［D］.Master＇s thesis.University of Alberta，2001.

［12］BERRYMAN J G.Long－wavelength propagation in composite elastic media.I.Spherical Inclusion and II.Ellipsoidal Inclusions［J］.Journal of the Acous－tical Society of America，1980（68B）：1809－1831.

［13］周巍，杨红霞.岩石裂隙对岩石的弹性性质及速度－孔隙率关系的影响［J］.石油地球物理勘探，2005，40（3）：334－338.

［14］XU S Y，PAYNE M A.Modeling elastic properties in carbonate rocks［J］.The Leading Edge，2009：66－74.

［15］KUMAR M，HAN D H.Pore shape effect on elastic properties of carbonate rocks［A］.SEG／Houston 2005Annual Meeting［C］.SEG，Society of Exploration Geophysicists，2005，1477－1480.

［16］赵克超，陈文学，陶果.利用Kuster－ Toksöz方程简化孔隙纵横比谱及判断储层孔隙类型［J］.西安石油大学学报，2009，24（1）：37－40.

［17］WHITE J E.Computed seismic speeds and attenuation in rocks with partial gas saturation［J］.Geophysics，2002（67）：1406－1414.

［18］SAYERS C M，RICKETT J E.Azimuthal variation in AVO response for fractured gas sands［J］.Geophysical Prospecting，1997，45（1）：165－182.

［19］AL－MARZOUG A M，NEVES F A，KIM J J.P－wave anisotropy from azimuthal AVO and velocity estimates using 3Dseismic data from Saudi Arabia［J］.Geophysics，2006，71（2）：E7－E11.

［20］阴可，杨慧珠.各向异性介质中的AVO［J］.地球物理学报，1998，41（3）：382－391.

［21］CHENG C H.Crack models for a transversely anisotropic medium［J］.Geophys Res，1993，98：675－684.

［22］ESHELBY J D.The determination of the elastic field of an ellipsoidal inclusion，and related problems［J］.Proc Royal Soc London，1957，241（A）：376－396.

［23］BROWN R，KORRINGA J.On the dependence of the elastic properties of a porous rock on the compressibility of the pore fluid［J］.Geophysics，1975（40）：608－616.

［24］吴国忱.各向异性介质地震波传播与成像［M］.东营：中国石油大学出版社，2006.

［25］RüGER A.Reflection coefficients and azimuthal AVO analysis in anisotropic media［D］. USA Golden：Colorado School of Mines，1996.