两个保序变换半群之间的同态

高京南,杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

两个保序变换半群之间的同态

高京南,杨秀良

(杭州师范大学理学院, 浙江 杭州 310036)

设On和IOn分别是集合Xn={1,2,…,n}上的保序变换半群和部分保序单变换半群.在此刻画了IOn到On的所有同态,On到IOn的所有同态.

同态;同态核;同余

1 引言和预备知识

令Xn={1,2,…,n}，集合Xn上所有保序变换在复合运算下构成的半群称为Xn的保序变换半群,记作On;Xn上的所有保序部分单变换在复合运算下构成的半群称为Xn的保序部分单变换半群,记作IOn.它们的许多性质已经被前人研究[1-8].特别的,On的自同态已被V.H.Fernandes等人在[1]中研究出来,IOn的自同态已被作者在[2]中研究出来.在此笔者将进一步研究On和IOn之间的同态.

本文的映射是右映射.令S,T为两个半群,φ:S→T为映射.若对任意的x,y∈S,都有(x)φ(y)φ=(xy)φ,则称φ为同态.由[3]知,On,IOn均为正则半群.

由[1],[4]知,On,IOn上的格林关系都为

αβ当且仅当im(α)=im(β);

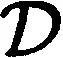
2 主要结果

在本文中得到下面两个结果：

定理1令φ:IOn→On为任一映射,φ是同态当且仅当φ是下面之一:

(1)存在幂等元e,f∈E(On),其中e≠f且ef=fe=f,有(1n)φ=e,(IOn{1n})φ=f;

(2)选取e∈E(On),对任意的α∈IOn,都有(α)φ=e.

定理2令φ:On→IOn为任一映射,φ是同态当且仅当φ是下面之一:

(1)存在幂等元e,f∈E(IOn),其中e≠f且ef=fe=f,有(1n)φ=e,(On{1n})φ=f;

(2)选取e∈E(IOn),对任意的α∈On,都有(α)φ=e.

3 定理1的证明

显然定理1中的(1),(2)均为同态.故只需证明除了(1),(2)外没有别的同态.

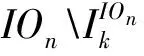
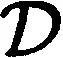
f≠f·d=(f)φ·d=(f·(d)φ-1)φ=f,

矛盾,因此l

(g)φ·f=(g)φ·(f)φ=(gf)φ=f=(fg)φ=(f)φ·(g)φ=f·(g)φ,

故有r(f)

im((δi)φ)∩im((δj)φ)=im(f) (i≠j).

综上所述,IOn到On的同态只有(1),(2)两种.

4 定理2的证明

保序变换半群On到保序部分单变换半群IOn的同态讨论类似IOn到On的同态.类似的,在On中有

引理3和引理4的证明类似引理1和引理2的证明.

令

im((εi)φ)∩im((εj)φ)=im(f′) (i≠j).

[1] Fernandes V H, Jesus M M, Maltcev V,etal. Endomorphisms of semigroups of order-preserving mappings[J]. Semigroup Forum,2010,81:277-285.

[2] 高京南,杨秀良.保序部分单变换半群的自同态[J].杭州师范大学学报：自然科学版，2013(3)：220-222.

[3] Ganyushkin O, Mazorchuk V. Introduction to classical finite transformation semigroup[M]. London: Springer Verlag,2009.

[4] Ganyushkin O, Mazorchuk V. On the structure ofIOn[J]. Semigroup Forum, 2003, 66: 455-483.

[5] Fernandes V H. The monoid of all injective order preserving partial transformations on a finite chain[J]. Semigroup Forum, 2001, 62: 178-204.

[6] Aizenstat A J. Homomorphisms of semigroups of endomorphisms of ordered sets[J]. Uch Zap Leningr Gos Pedagog Inst,1962:238,38-48.

[7] Howie J M. Fundamentals of semigroup theory[M]. New York: Oxford University Press, 1995.

[8] Timothy L, Andrew S. The endomorphisms of a finite chain form a Rees congruence semigroup[J]. Semigroup Forum, 1999,59: 167-170.

HomorphismsofTwoOrder-preservingTransformationSemigroups

GAO Jingnan, YANG Xiuliang

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

OnandIOnare the order-preserving transformation semigroup and partial order-preserving single transformation semigroup onXn={1,2,…,n} respectively. This paper described all homorphisms fromIOntoOnand the homorphisms fromOntoIOn.

homorphism; kernel; congruence

2012-12-02

杨秀良(1963—),男,教授,博士,主要从事半群代数研究.E-mail：yxl@hznu.edu.cn

10.3969/j.issn.1674-232X.2013.05.007

O152.7MSC201043A22

A

1674-232X(2013)05-0418-04