J-Boolean like环

秦 蕊

(杭州师范大学理学院, 浙江 杭州 310036)

J-Boolean like环

秦 蕊

(杭州师范大学理学院, 浙江 杭州 310036)

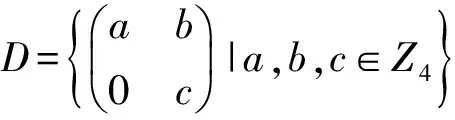
首先给出相关定义：

定义1设D是一个环,C是D的一个子环,而且1D∈C,

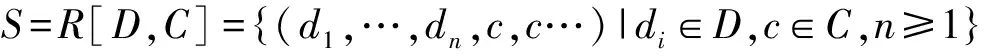
R[D,C]中加法和乘法分别定义为对应分量的加法和乘法，则R[D,C]关于所定义的加法与乘法构成一个环.

定义2称环R为Boolean-like环,如果R是特征为2的交换环并且对所有a,b∈R都有ab(1-a)(1-b)=0.[3]

下面把Boolean-like环推广到一般结合环上,并引入一个新的定义：

定义3如果对任意环R中元素a,b都有(a-a2)(b-b2)∈J(R),那么R称为J-Boolean like环.

引理1若S=R[D,C],则J(S)=R[J(D),J(D)∩J(C)].

定理1设D是一个环,C是D的一个子环,则R[D,C]是一个J-Boolean like环的充要条件为(a)C,D是J-Boolean like环,(b)J2(C)⊆J(D).

证明(⟹)对任意的a,b∈D,设x=(a,0,0,0,…),y=(b,0,0,0…)有

(x-x2)(y-y2)=((a-a2)(b-b2),0,0,0…).

因为R[D,C]是一个J-Boolean like环,由引理1知(a-a2)(b-b2)∈J(D),所以D是一个J-Boolean like环.

对任意的a,b∈C,设x=(a,a,…,a),y=(b,b,…,b),于是

(x-x2)(y-y2)=((a-a2)(b-b2),(a-a2)(b-b2),…,(a-a2)(b-b2))∈J(R[D,C]),

这样(a-a2)(b-b2)∈J(D)∩J(C),也就是(a-a2)(b-b2)∈J(C),所以C是一个J-Boolean like环.

对任意的x,y∈J(C),下证xy∈J(D).设x=(a,a,…,a),y=(b,b,…,b),则

(x-x2)(y-y2)=((a-a2)(b-b2),(a-a2)(b-b2),…,

(a-a2)(b-b2))∈J(S)=R[J(D),J(D)∩J(C)],

所以(x-x2)(y-y2)∈J(D),即为(1-x)xy(1-y)∈J(D).

因为x,y∈J(C),所以1-x,1-y∈U(C)⊆U(D),这样就存在r,s∈D使

r(1-x)=1,(1-y)s=1,

并且r(1-x)xy(1-y)s∈J(D),所以xy∈J(D),即证J2(C)⊆J(D).

(⟸)对任意的R[D,C]中x=(a1,a2,…,an,a,a…),y=(b1,b2,…,bn,b,b…),r=(r1,r2,…,rn,s,s…),有

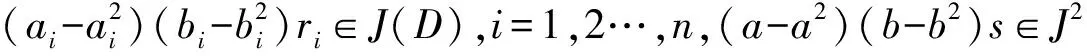
1-[(x-x2)(y-y2)r]2∈U(S).

因此,1-(x-x2)(y-y2)r∈U(S),所以(x-x2)(y-y2)∈J(R),即是R[D,C]是一个J-Boolean like环.

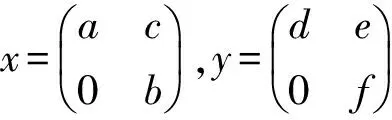
所以J2(C)⊆J(D).

由定理1知，R[D,C]是J-Boolean like环.

这样有J2(C)⊆J(D).

显然,D,C都是J-Boolean like环,且C⊆D,由定理1知,R[D,C]是J-Boolean like环.

引理2设B为一个环,对任意a,b∈J(B)有ab≡ba(modJ(B)).

引理3如果B[i]是J-Boolean like环，那么2i3-i2≡i4(modJ(B[i]).)

证明由于(i-i2)2=i2-2i3+i4∈J(B[i]),所以2i3-i2≡i4(modJ(B[i]).

引理4如果B/J(B)是Boolean环，那么2∈J(B),即2≡0(modJ(B)).

证明因为a∈J(B),所以1+a∈U(B).这样x+(1+a)-1by=(1+a)-1,

进而cx+c(1+a-1)by=c(1+a)-1.与第二个方程作差得,

[c(1+a)-1b-1-a]y=c(1+a)-1,

令d=c(1+a)-1b-a,由于a,b,c∈J(B),所以d∈J(B),可以得到d-1可逆,最后解得

y=(d-1)-1c(1+a)-1.

将其代入原方程组可得x=-c-1(1+a)(d-1)-1c(1+a)-1.

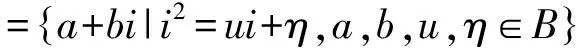
证明(⟹)由i2=ui+η,知i4=u2i2+uηi+ηui+η2.而

u≡u2(modJ(B),η≡η2(modJ(B),uη≡ηu(modJ(B)),

所以i4≡ui2+η(modJ(B),进而i4≡u(ui+η)+η=ui+uη+η(modJ(B)).

由引理3，i4≡2i3-i2(modJ(B)),也就是

i4≡(2i-1)(ui+η)≡2ui2+(2η-u)i-η≡2u(ui+η)+(2η-u)i-η

≡2ui+2uη+(2η-u)i-η≡ui+2uη+2ηi-η(modJ(B)),

这样i4≡ui+uη+η≡ui+2uη+2ηi-η(modJ(B)),即为

uη≡-2ηi+2η,

所以uη∈J(B[i])+J(B).

下证J(B)[i]∈J(B[i]),即证对任取的B[i]中元素m+ni,e+fi有

1-(m+ni)(e+fi)∈U(B[i]).

那么在B[i]中存在x+yi,使得[1-(m+ni)(e+fi)](x+yi)=1.因为

1-(m+ni)(e+fi)=(1-me-nfη)-(mf+ne-nfu)i,

所以

由于me+nfη,(mf+ne-nfu)η,(me+nfη)+(mf+ne-nfu)η∈J(B[i]),

所以由引理6知此方程组有解，也就证得

1-(m+ni)(e+fi)∈U(B[i]).

所以J(B)[i]∈J(B[i]).而J(B)⊆J(B)[i]⊆J(B[i]),所以

uη∈J(B[i])

任取r∈B⊆B[i],有1-uηr∈U(B[i]),这样

(1-uηr)(a+bi)=1,

也就是 (1-uηr)a+(1-uη)rbi=1,

可以看出 1-uηr∈U(B),

最后uη∈J(B).

(⟸)任取B[i]中元素a+bi,x+yi,设

A=(a+bi)-(a+bi)2≡b(i-i2)(modJ(B)),

同理B=(x+yi)-(x+yi)2≡y(i-i2)(modJ(B)).

因此AB=by(i-i2)2.

由于 (i-i2)2=i2-2i3+i4≡i2+i4≡ui+u2i+uη+η≡uη(modJ(B)),

所以AB≡byuη(modJ(B)),即证得AB∈J(B[i])+J(B)[i],

因为J(B)[i]∈J(B[i]),

所以AB∈J(B[i]),所以B[i]是J-Boolean like环.

证明(⟹)首先B为J-Boolean like环知,对B中任意元素a有

(a-a2)2∈J(B).

因为J(B)是所有极大理想的交,那么对任意极大理想M,(a-a2)2∈M(见[1]),

进而a-a2∈∩M=J(B),所以

a-a2∈J(B).

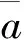
由定理2知,如果B[i]是J-Boolean like环当且仅当uη∈J(B).

证明(⟹)由于B[i]是J-Boolean like环，所以(i-i2)(i-i2)∈J(B[i]),即

i2+i4∈J(B[i]).

设i2+i4=a,则a∈J(B[i]),由于B是Boolean环,i2=ui+η,所以

ui2=u(ui+η)=u2i+uη=ui+uη

i4=(ui+η)2=u2+2uiη+η2=ui2+η=ui+uη+η

而a-i2=i4,故a-ui-η=ui+uη+η.

因为u,η均为Boolean环B中元素，进而a=uη∈J(B).

反之显然成立，这样定理得证.

证明由于B为Boolean环，那么对于B中元素u,η有(1-uη)2=1-uη.

因为uη∈J(B[i]),所以存在B中元素c,使(1-uη)2c=(1-uη)c=1,

进而1-uη=1,也就是uη=0,即B[i]为Boolean-like环，反之显然.

参考文献:

[1] Foster A L. The idempolent elements of a commutative ring form a Boolean algebra ring duality and transformation theory [J]. Duke Math,1945,12(1):143-152.

[2] Foster A L. The theory of Boolean-like rings [J]. Transactions of the American Mathematical Society,1946,59(1):166-187.

[3] Swaminathan V. On Foster’s Boolean like rings [J]. Math Seminar Note,1980,8(2):347-367.

[4] Samuel Bourne. The Jacobson radical of a semiring [J]. Proc Natl Acad Sci USA,1951,37(3):163-170.

[5] Swaminathan V. Injective and projective Boolean-like rings [J]. Journal of the Australian Mathematical Society,1982,33(1):40-49.

[6] Cheng Gongpin. The structure of ringR[D,C] and its characterizations [D]. Nanjing: Southeast University,2006:4-13.

2012-11-07

秦 蕊(1987—),女,基础数学硕士研究生,从事代数研究.E-mail: bhqinrui@126.com

Boolean环;Boolean-like环;J-Boolean like环；Jacobson根；R[D,C]环

O153.3MSC201013M05

A

1674-232X(2013)05-0413-05

[2].

J-BooleanLikeRing

QIN Rui

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

10.3969/j.issn.1674-232X.2013.05.006

Booleanring;Boolean-likering;J-Booleanlikering;Jacobsonradical; R[D,C]ring