Ga9-nAsn(n=0~9)系列团簇能量和稳定性的研究
姜 科,刘乔升,杨建宋
(1. 杭州师范大学经亨颐学院,浙江 杭州 311121;2. 杭州师范大学理学院,浙江 杭州 310036)
Ga9-nAsn(n=0~9)系列团簇能量和稳定性的研究
姜 科1,刘乔升1,杨建宋2
(1. 杭州师范大学经亨颐学院,浙江 杭州 311121;2. 杭州师范大学理学院,浙江 杭州 310036)
采用基于第一性原理的ADF程序,对Ga9-nAsn(n=0~9)系列团簇的基态结构、能量、稳定性和电离能等物理性质进行了系统的计算和分析.结果表明,随着n的增加,团簇的结合能将呈线性增加,电离能在5.5和7 eV左右波动,亲和能在2.5~3 eV波动,电离能明显大于亲和能.在n=5和n=6附近,Ga9-nAsn(n=0~9)团簇的稳定性最高.
砷化镓团簇;基态结构;稳定性
0 引 言
对砷原子和镓原子数目不相等的GamAsn团簇,近年来也有人做过一些研究.2008年马德明利用密度泛函理论(DFT)对GamAsn(m=1、2;n=1~5)的几何结构和稳定性进行了研究[21-22],并在B3L YP/6-31G*水平上做了结构优化及频率分析,在得到GamAsn(m=1、2;n=1~5)的基态和亚稳态的基础上,发现团簇的稳定性随着其中原子数的增多而增强,总原子数相同的团簇中,As原子多的团簇比Ga原子多的团簇更稳定,并且发现团簇的HOMO-LUMO能隙随原子数的增加呈现奇偶交替的变化规则.马德明等也对Ga2Asn(n=1~5)的正负离子团簇展开了研究,发现团簇的稳定性随n的增大呈现奇偶交替变化,对负离子团簇,总原子数为奇数的原子相对比较稳定,而对正离子团簇情况则正好相反.类似的研究在氮化镓和磷化镓团簇中也有一些报道.但对砷化镓的不对称团簇,所做工作还不是很多,特别是对团簇中原子数目稍大一些的全系列研究,见到的并不多.
本文将采用基于第一性原理的阿姆斯特丹密度泛函程序(ADF),对Ga9-nAsn(n=0~9)系列团簇的基态结构、能量、稳定性、电离能和亲和势等重要物理性质进行计算和分析,拟通过几十万次的计算来得到各个中性Ga9-nAsn(n=0~9)团簇的基态结构,分析其基态能量和其他物理性质随着成分比变化的一般规律和偏离情况,计算其一阶和两阶的偏离能以及HOMO-LUMO能隙,讨论其稳定性随团簇成分而发生变化的规律.同时也将计算各个Ga9-nAsn(n=0~9)团簇的电离能和亲和势,研究这些团簇的电离性质随团簇成分变化而发生的变化.
1 方 法
优化Ga9-nAsn(n=0~9)团簇计算采用阿姆斯特丹密度泛函程序(ADF,版本号2007.01).该程序基于第一性原理,采用在LDA基础上依赖于电荷密度梯度的广义梯度近似(GGA)和Becke-Perdew交换关联泛函方法,以Becke的梯度修正对交换能作局域描写,用Perdew的梯度修正对相关能作局域表达[23-24].ADF采用Slater型函数描述原子轨道,较高斯函数更接近真实情况.分子轨道被展开为一套非约化的slater型轨道:TZ2P基组是一个具有两套极化函数的三重ζ全电子基组,将被用来修正分子密度并描写在每一个自洽场周期中的库伦势和交换势,自洽场将收敛到10-7.对内层电子的处理用到了冻结核近似,即在优化计算时砷原子和镓原子直到3d轨道都将被冻结.
因为砷化镓Ga9-nAsn(n=0~9)团簇是由两种元素构成的非对称团簇,利用第一性原理去全面探求其基态结构是一件十分困难的事情,两种元素下通过位置交换引起的各种组合方式非常多,从而使计算的工作量十分巨大.对用第一性原理探索团簇的基态,通常会用到遗传算法和模拟退火算法.遗传算法在计算结构的全局优化上用得非常多,其要点是经过优化计算后父母团簇的重要性质会遗传给亲子团簇,但那些较小的团簇做结构优化后常会出现较大畸变,从而丢失了父辈团簇的特点,这是它的困难之处.在模拟退火方法中,随着系统的温度下降,将出现更多的低能量状态,并在绝对零度时系统占据能量最低的状态.但这是一个渐进的过程,以此方法来实现全局最低的优化计算是需要无限多数量的温度台阶,实际的计算量相当大.
2 结果及讨论
本文的优化计算过程考虑到了遗传算法和模拟退火算法的优势和困难,对Ga9-nAsn(n=0~9)初始几何构形的选择采用了两种途径:首先利用课题组丁望峰博士自编的随机计算程序auto1.2进行较大范围的随机计算,选择了3种典型的团簇的初始空间形状,即球状、笼状和盒状.在团簇初始配置的原子位置设定上,球(或盒)的尺寸和相邻两个原子之间距离的选择要顾及到避免重叠同时也避免发生散包现象.所谓的笼状结构就是把Ga9-nAsn(n=0~9)团簇中的所有原子安排在一个球或椭球的表面.利用随机优化计算,笔者获得了数以万计的团簇结构,通过挑选和分析,在其中寻找能量最低的结构作进一步的分析计算.另一种方法是利用对称性或利用前人已经求得的一些低能态几何结构来构造Ga9-nAsn(n=0~9)的初始几何构形.这时采用替代或吸附的方法.例如Ga9-nAsn,可以从已经得到的Ga9-n+1Asn-1基态团簇出发,用一个砷原子去取代一个镓原子,在所有可能的替代结构中寻找能量最低的结构;吸附方法指的是在已经求得的Ga8-nAsn基态结构的吸附点上,增加一个砷原子或镓原子形成新的Ga9-nAsn团簇,再从中寻找能量比较低的Ga9-nAsn(n=0~9)结构.采用这两种方法构造Ga9-nAsn(n=0~9)团簇的初始几何构形,并以ADF程序包进行几何优化.为了确保所得到的结构是稳定的,最后还做了一个频率计算,剔除所有出现了负频率的情形.由此所得的Ga9-nAsn(n=0~9)团簇的最低能量结构被视作该团簇的基态结构.在此基础上,本文进一步计算了Ga9-nAsn(n=0~9)各团簇基态结构下的绝热电离势(IPs)、绝热电子亲和势(EAs)以及最高占据分子轨道(HOMO)和最低未占据分子轨道(LUMO)之间的能隙(Eg).
2.1Ga9-nAsn(n=0~9)团簇的基态结构
表1给出了Ga9-nAsn(n=0~9)团簇基态结构下各原子的坐标和团簇的结构图.

表1 Ga9-nAsn基态结构团簇中各原子的坐标参数Tab. 1 The coordinate parameters of atoms of ground state structure of Ga9-nAsn(n=0~9) clusters
续表

结构原子xyz结构图n=5GaAsGaAsAsAsGaGaAs1.4513650.5587962.5851950.343389-0.102399-1.173379-2.298859-2.0918920.416083-2.557010-0.7933550.3311741.739965-0.296741-1.5195571.3067600.1262752.015295-0.6691691.608925-0.4310411.183071-2.126232-0.125458-0.6424122.231198-1.307128n=6GaGaAsAsAsAsGaAsAs0.5866342.151596-0.0355871.135293-0.312952-2.327805-1.479370-0.070172-2.014284 0.8267360.2733102.055453-1.7824510.410145-0.633358-1.607023-1.9537521.028319-2.2543500.5185150.389115-0.9354422.3367141.137445-1.6433931.240830-0.790584n=7AsGaAsAsGaAsAsAsAs-1.896351-0.494659-0.2866520.4396392.6341720.7579271.914512-1.7564140.153687 0.6028052.697737-2.0651220.118610-1.6940280.2106831.097808-0.009324-2.282087 1.009406-0.206057-1.3490471.796467-0.029690-2.088481-0.068326-1.4201881.113492n=8AsGaAsAsAsAsAsAsAs-0.0515811.0933521.989534-1.459143-0.274822-1.477650-0.3063251.865016-2.154962 2.0355400.1724440.9550640.234023-1.969190-0.580275-2.464132-1.5025021.103725-0.9197522.4725700.021466-2.008478-1.6383611.9756620.833661-0.3899640.265473n=9AsAsAsAsAsAsAsAsAs0.726535-0.1576622.7721661.706787-0.022719-2.529734-2.2283480.453714-1.638308-1.6201960.4720761.369673-0.6713131.111316-0.032871-0.0745412.291138-2.144694 0.6750551.851054-0.324702-1.434337-1.9683170.993470-1.5163820.230605-0.191181
注:图中浅色球代表镓原子,深色球表示砷原子;坐标单位为10-10m.
从结构图中可见,Ga9-nAsn(n=0~9)系列团簇的基态结构从n=0时9个镓原子构成的带一个帽原子的菱柱结构变化到n=9时9个砷原子构成的一个底面为五边形的多面体结构.在n=5和n=6时,表现出比较致密的笼状多面体结构.各Ga9-nAsn(n=0~9)团簇基态结构的对称性可见表2.

表2 Ga9-nAsn(n=0~9)团簇基态结构的对称性Tab. 2 The symmetry of ground state structure of Ga9-nAsn(n=0~9) clusters
2.2Ga9-nAsn(n=0~9)团簇的能量和其他物理性质
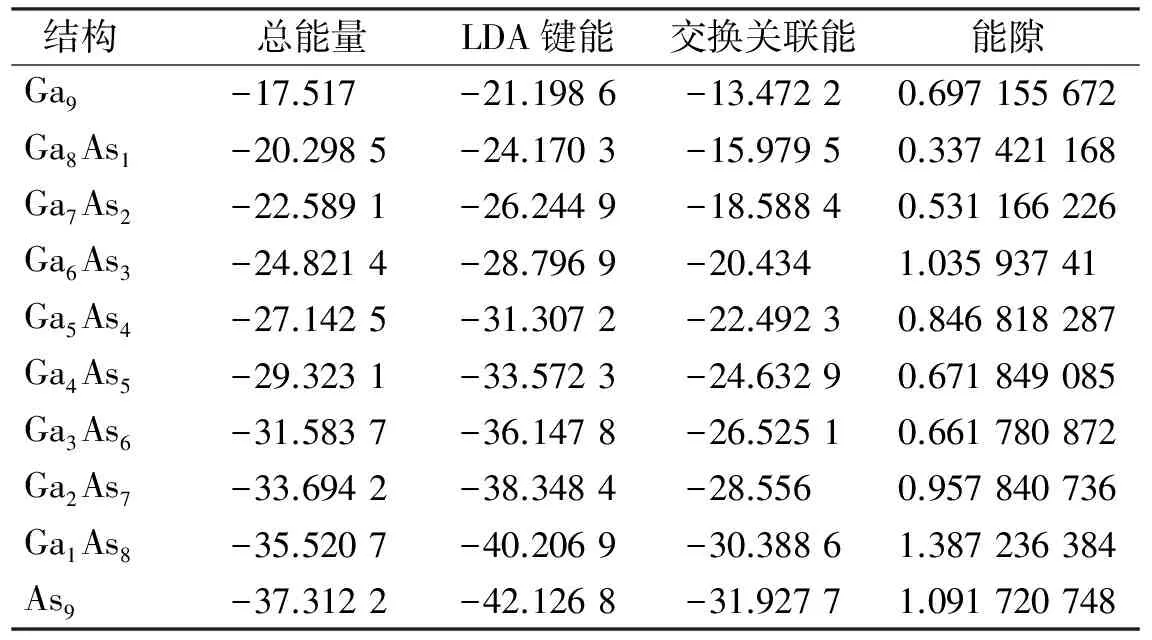
表3 Ga9-nAsn基态结构团簇的物理性质Tab. 3 Physical properties of ground state structure of Ga9-nAsn(n=0~9)series clusters /eV
表3给出Ga9-nAsn(n=0~9)团簇基态结构下的总能量、LDA键能、交换关联能以及HOMO-LUMO能隙.由表3 可见,随着镓原子逐渐被砷原子取代,团簇的总能量、LDA键能和交换关联能几乎呈线性地下降.而HOMO-LUMO能隙总体呈现出一种起伏有升的态势.
从图1a可见随着n的增加,团簇的总能量几乎呈线性下降(即结合能呈线性增加).用origin软件对此进行线性拟合,得到y=-18.088 28-2.198 21x(式中截距、斜率的标准偏差分别为0.203 9,0.038 19).笔者计算了各团簇能量与拟合值的差异(图1b)和团簇能量的二级能量差(图1c).依据数据拟合,用一个砷原子取代Ga9-nAsn团簇中的镓原子,团簇的结合能将增加2.198 eV左右,从图1b可见,当n=6时,替代一个镓原子,增加的结合能出现一个高峰;从图1c见到,在n=3和n=5位置上,出现最低值.结合这两图的特点,笔者认为,在n=5和n=6处,团簇的稳定性将最高.这一点也可由冻结核模型得到解释,在这10个结构中,考虑到在作优化计算时把砷原子和镓原子的3d以内壳层作了冻结近似,因此Ga9-nAsn(n=0~9)系列团簇的价电子数目将分别为9,11,13,15,17,19,21,23,25,27.

图1 Ga9-nAsn(n=0~9)基态结构团簇的总能量、电离能等物理性质Fig. 1 Total-energy,ionization-energy and other physical properties of ground state structure of Ga9-nAsn(n=0~9)series clusters
从图1d可见,电离能在5.5,7 eV左右波动,在n=2和n=6附近出现高峰,总体随n的增加有所上升,从n=7到n=9,电离能从5.8 eV直接增加到7 eV.但图1e中的亲和能在2.5~3 eV波动,明显小于电离能,说明Ga9-nAsn(n=0~9)团簇吸附一个电子要比丢失一个电子容易得多,亲和能也在n=2和n=6附近出现高峰,在n=8出现一个较深的低谷.电离能和亲和能同在n=6附近出现峰点,这与结合能一级差在n=6出现最大值是对应的,表明Ga9-nAsn(n=0~9)系列团簇在n=6时是比较稳定的.
HOMO-LUMO能隙在0.4~1.4 eV之间随n的增加呈现波浪式的增长.在n=1和n=5~6处出现了两个低谷,而在n=3和n=8处出现两个峰值(图1f).
3 结 论
本文用基于第一性原理的ADF程序,对Ga9-nAsn(n=0~9)系列团簇的基态结构、总能量、稳定性和电离能、亲和势等物理性质进行了计算和讨论.在对团簇的基态结构探求中,采用了球状、盒状和笼状框架下的随机计算和从对称性或前人已得的低能态结构进行替换或吸附.计算表明:随着n的增加团簇的结合能将几乎呈线性增加,用一个砷原子取代Ga9-nAsn团簇中的镓原子,团簇的结合能将增加2.198 eV左右,从能量的一阶差分图和二阶能量差上可以看到,在n=5和n=6附近,团簇的稳定性最高,这时的基态Ga4As5和Ga3As6团簇呈现C2或C5对称性.Ga9-nAsn(n=0~9)系列团簇的电离能在5.5和7 eV左右波动,亲和能在2.5~3 eV波动,电离能明显大于亲和能,并都在n=6附近呈现高峰.
李宝兴教授和丁望峰博士在本论文研究工作中给予指导和帮助,一并致谢!
[1] Mingo N. Thermoelectric figure of merit and maximum power factor in III-V semiconductor nanowires[J]. Appl Phys Lett,2004,84(14):2652-2654.
[2] Howes M J, Morgan D V. Gallium arsenide: materials, devices and circuits[M]. New York: John Wiley & Sons Inc,1985:35-119.
[3] O’Brien S C, Liu Y, Zhang Q,etal. Supersonic cluster beams of III-V semiconductors: GaxAsy[J]. J Chem Phys,1986,84(7):4074-4079.
[4] Al-Laham M A, Raghavachari K. Theoretical study of Ga4As4, Al4P4, and Mg4S4clusters[J]. J Chem Phys,1993,98(11):8770-8776.
[5] Song K M, Ray A K, Khowash P K. On the electronic structures of GaAs clusters[J]. J Phys B,1994,27(8):1637-1648.
[6] Lou L, Wang L, Chibante L P F,etal. Electronic structure of small GaAs clusters[J]. J Chem Phys,1991,94(12):8015-8020.
[7] Yi J Y. Atomic and electronic structures of small GaAs clusters[J]. Chem Phys Lett,2000,325:269-274.
[8] Zhao Jijun, Xie Ruihua, Zhou Xiaolan,etal. Formation of stable fullerenelike GanAsnclusters(6≤n≤9): gradient-corrected density-functional theory and a genetic global optimization approach[J]. Phys Rev B,2006,74(3):035319.
[9] Karamanis P, Bégué D, Pouchanc C. Ab initio finite field(hyper)polarizability computations on stoichiometric gallium arsenide clusters GanAsn(n=2~9)[J]. J Chem Phys,2007,127(9):094706.
[10] Zhao Wei, Cao Peilin, Li Baoxing,etal. Study of the stable structures of Ga4As4cluster using FP-LMTO MD method[J]. Phys Rev B,2000,62(24):17138-17143.
[11] Zhao Wei, Cao Peilin. Study of the stable structures of the Ga5As5cluster using the full-potential linear-muffin-tin-orbital molecular-dynamics method[J]. J Phys: Condens Matter,2002,14(1):33-44.
[12] Zhao Wei, Cao Peilin. Study of the stable structures of Ga6As6cluster using FP-LMTO MD method[J]. Phys Lett A,2001,288(1):53-57.
[13] Zhao Wei, Cao Peilin, Duan Weihua. Study of structure characteristics of the Ga8As8cluster[J]. Phys Lett A,2006,349:224-229.
[14] Liu Y, Zhang Q L, Tittle F K,etal. Photodetachment and photofragmentation studies of semiconductor cluster anions[J]. J Chem Phys,1986,85(12):7434-7441.
[15] Taylor T R, Gómez H, Asmis K R,etal. Photoelectron spectroscopy of GaX2-, Ga2X-, Ga2X2-, and Ga2X3-(X=P,As)[J]. J Chem Phys,2001,115(10):4620-4631.

[17] Yang Jiansong, Li Baoxing, Zhan Shichang. Study of GaAs cluster ions using FP-LMTO MD method[J]. Phys Lett A,2006,348:416-423.
[18] 杨建宋.带电对Ga7As7团簇基态结构的影响[J].杭州师范大学学报:自然科学版,2012,11(6):545-551.

[20] Gutsev G L, O’Neal R H, Saha B C,etal. Optical properties of (GaAs)nclusters(n=2~16)[J]. J Phys Chem A, 2008,112(43):10728-10735.
[21] 马德明,李恩玲,施卫,等.密度泛函理论对GamAsn团簇的结构及稳定性的研究[J].原子与分子物理学报,2008,25(4):984-990.
[22] 马德明,施卫,李恩玲,等.Ga2Asn离子团簇结构及光电子能谱研究[J].光学学报,2009,29(4):1032-1037.
[23] Becke A D. Density-functional exchange-energy approximation with correct asymptotic behavior[J]. Phys Rev A,1988,38(6):3098-3100.
[24] Perdew J P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas[J]. Phys Rev B,1986,33(12):8822-8824.
[25] Ding Wangfeng, Li Baoxing. A first-principles study of AlnSim-nclusters (m=6,9,10;n≤m)[J]. J Mol Struc:THEOCHEM,2009,897:129-138.
TheStudyofEnergyandStabilityofGa9-nAsn(n=0~9)SeriesClusters
JIANG Ke1, LIU Qiaosheng1, YANG Jiansong2
(1.Jing Hengyi Honors College, Hangzhou Normal University, Hangzhou 311121, China; 2.College of Science, Hangzhou Normal University, Hangzhou 310036, China)
The ground-state structure, energy, stability, ionization energy and other physical properties of Ga9-nAsn(n=0~9) series clusters were calculated and analyzed using ADF program based on first principle. The results show that the binding energy of the cluster increases in linear with the increase ofn, the ionization energy fluctuates between 5.5 to 7 eV, and affinity energy waves from 2.5 to 3 eV, the ionization energy is significantly greater than the affinity. The stability of the cluster is the highest nearn=5 andn=6.
gallium arsenide cluster; ground state structure; stability
2013-05-01
国家自然科学基金项目(11274084).
杨建宋(1957—),男,教授,主要从事凝聚态物理和理论物理研究.Email: yjs@hznu.edu.cn
10.3969/j.issn.1674-232X.2013.06.008
O561
A
1674-232X(2013)06-0517-07
——以物质结构与性质模块“元素周期律”教学为例

