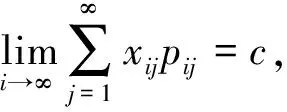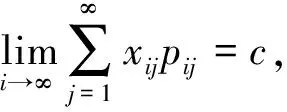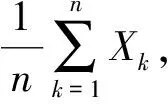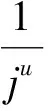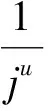关于一类特殊随机变量的切比雪夫大数定律推论
马安庆,陆 竞,谷 峰
(杭州师范大学理学院,浙江 杭州 310036)
关于一类特殊随机变量的切比雪夫大数定律推论
马安庆,陆 竞,谷 峰
(杭州师范大学理学院,浙江 杭州 310036)
针对可能取值有无限个的离散型随机变量,以数学分析中的级数为工具推演切比雪夫大数定律,研究了期望、方差及相关的序列,得到了关于离散型随机变量有针对性的推论.
级数;与级数相关的序列;敛散性;期望;方差;与期望方差相关的序列
切比雪夫大数定律是概率论中的重要内容,适用于各种概型,具有一般性,将它在离散型随机变量(以下简称特殊随机变量)环境中具体化可得出更有针对性的推论.由于该定律与期望、方差及相关序列有关,而特殊随机变量的期望、方差及相关的序列又与级数、与级数相关的序列存在联系.因此本文通过切比雪夫大数定律中的问题来寻找研究方向,以级数为问题的解决提供理论依据,最终达到推演该定律的目的.
1 相关基础知识
切比雪夫大数定律[1]设独立随机变量序列X1,X2,…,Xi,…的数学期望E(X1),E(X2),…,E(Xi),…与方差D(X1),D(X2),…,D(Xi),…都存在,并且方差都是一致有上界的, 即存在某一常数K,使得D(Xi) (1) 下文用到的阶的估计的基本知识参见文献[2]. 以下为级数及与级数相关序列的结论. 为了使结论便于推演切比雪夫大数定律,在此以E(Xi),i=1,2,3,…存在为前提来讨论问题. 由ε的任意性可知, 经进一步观察归纳猜想证明得以下结论. 现将相关的基础结论与切比雪夫大数定律及切比雪夫不等式相结合,得出具有特殊随机变量特色的推论. 相比于辛钦大数定律,推论1不要求随机变量服从同一分布,不要求数学期望相同. 由例题可知该推论相比于切比雪夫大数定律不要求方差有界. 由上述结论可得出的推论不止两个,限于篇幅不能一一列举,遇到具体问题时可根据期望、方差及相关序列的特点选取以上的结论来解决问题. [1] 沈恒范.概率论与数理统计[M].5版.北京:高等教育出版社,2011:159. [2] 沈忠华,虞旦盛,于秀源.数学分析问题讲析[M].杭州:浙江大学出版社,2010:1. [3] 盛骤,谢式千,潘承毅.概率论与数理统计[M].4版.北京:高等教育出版社,2008:119. ChebyshevLawofLargeNumbersforaClassofSpecialRandomVariables MA Anqing, LU Jing, GU Feng (College of Science,Hangzhou Normal University, Hangzhou 310036, China) Possible values have infinite number of discrete random variables, so that this paper deduced Chebyshev law of large numbers with series, studied expectation, variance and relevant sequences, and obtained the inference that special random variables had pertinence. series; sequences correlative with series; convergence and divergence; expectation; variance; sequences correlative with expectation and variance 2013-05-23 陆 竞(1958—),男,副教授,主要从事函数论研究.E-mail:wllujing@sina.com 10.3969/j.issn.1674-232X.2013.06.006 O211.4MSC201060F99 A 1674-232X(2013)06-0507-06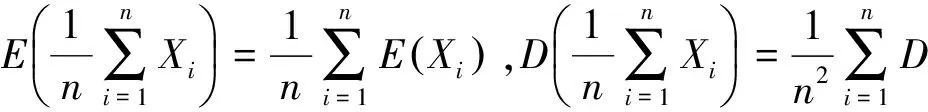
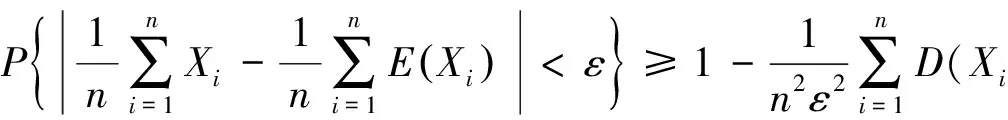
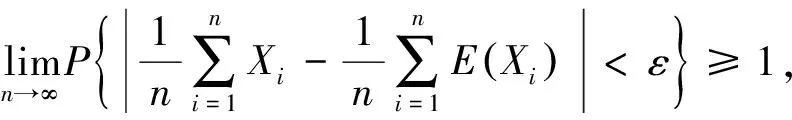
2 研究对象的引入
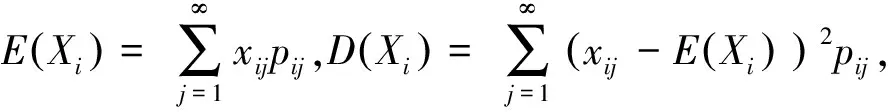
3 相关结论
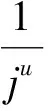


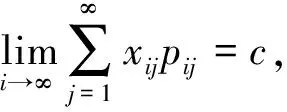
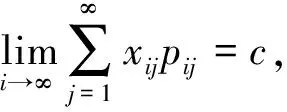
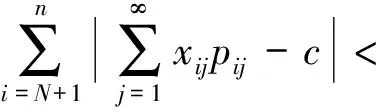
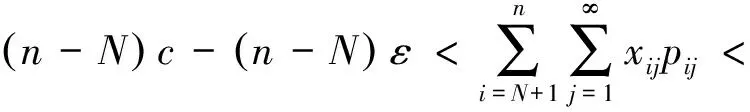

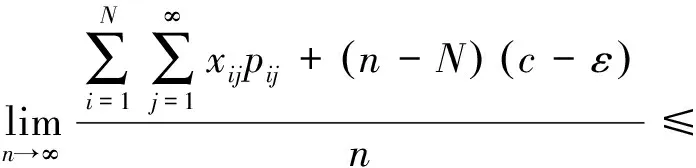
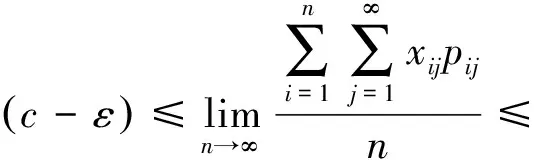

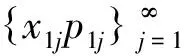


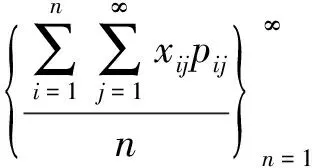
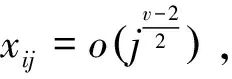
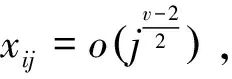
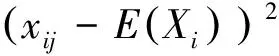

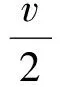




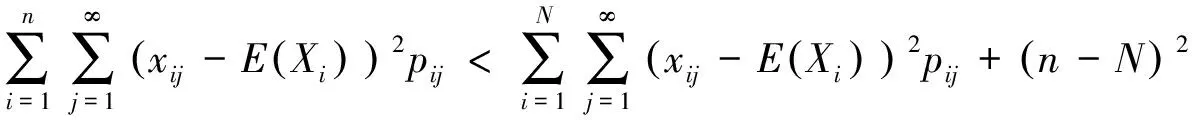
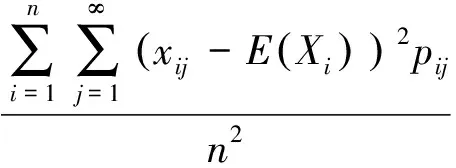
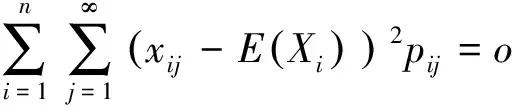
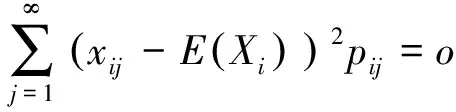
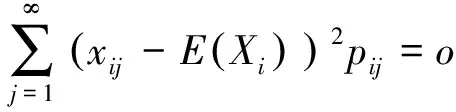
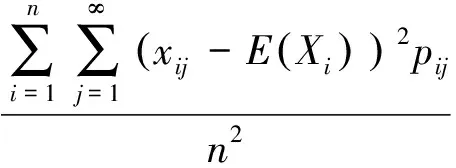
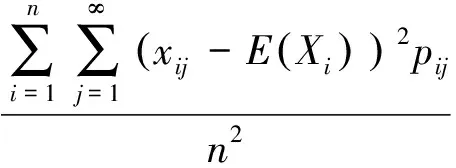
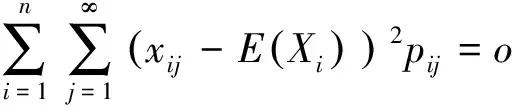
4 相关推论