高中数学竞赛客观题中的全对称与轮换对称

●王 华 王延敏

(凤鸣高级中学 浙江桐乡 314500)

高中数学竞赛客观题中的全对称与轮换对称

●王 华 王延敏

(凤鸣高级中学 浙江桐乡 314500)

在高中数学竞赛中，若满足f(a,b,c)=f(b,c,a)=f(c,a,b)，则称为轮换对称；若在轮换对称的基础上满足f(a,b,c)=f(b,a,c)，则称为全对称．无论是在高中数学联赛还是在国际数学奥林匹克竞赛中，全对称与轮换对称都占据着一定的地位．它在客观题中主要以求最值的形式出现，对学生来说，“全对称与轮换对称”客观题都是难题．下面通过对高中数学竞赛客观题中典型例题的分析，盘点“全对称与轮换对称”客观题的最佳解题策略．

一、高中数学竞赛客观题中的“全对称”

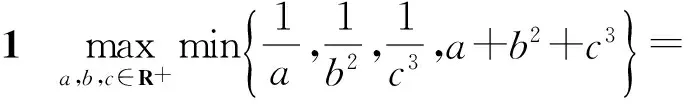
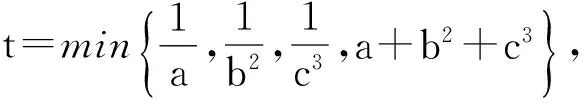
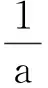
从而

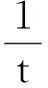
于是

得

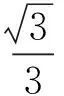
解法2由题意可知，a,b2,c3是全对称，可知取最值只会在三者相等时取到，令

则

a=b2=c3，

从而

又a>0，得

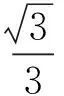
点评解法1中利用解不等式求出其最大值，解法2中巧妙地利用原式取得最大值时a,b2,c3三者相等.

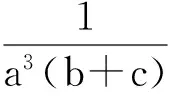
解法1

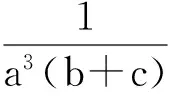
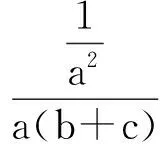
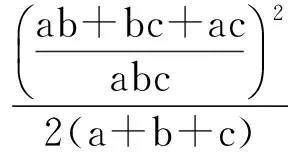
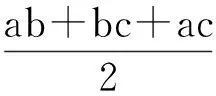
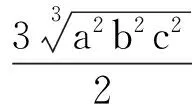
解法2由题意可知，a,b,c是全对称，可知最小值只会在三者相等时取到，即a=b=c，而abc=1，因此a=b=c=1.此时原式的最小值为

点评解法1中2次利用基本不等式求出其最小值，解法2中巧妙地利用原式取得最大值时a,b,c三者相等.

例3设n为自然数，对于任意实数x,y,z恒有(x2+y2+z2)2≤n(x4+y4+z4)成立，则n的最小值为______.

解法1令a=x2,b=y2,c=z2，则题设不等式变为

(a+b+c)2≤n(a2+b2+c2).

一方面，

(a+b+c)2= a2+b2+c2+2ab+2bc+2ac≤

a2+b2+c2+(a2+b2)+(b2+

c2)+(a2+c2)=

3(a2+b2+c2),

当n=3时不等式成立；

另一方面，当a=b=c>0时题设不等式可化为9a2≤3na2，必有n≥3.

故n的最小值为3.

解法2由题意可知，x,y,z是全对称，可知最小值只会在三者相等时取到，即x=y=z，故题设中不等式等号成立时，n的最小值为3.

点评解法1中利用两边夹原理求出其最小值，解法2中巧妙地利用原式取得最大值时x,y,z三者相等.

2 高中数学竞赛客观题中的“轮换对称”

例4

A．2B．4C．6D．8

解法1f(x)=

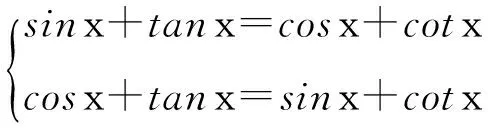
两式相减得

sinx-cosx=cosx-sinx，

即

sinx=cosx.

因为

所以

从而

故选B.

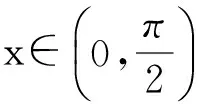
sinx=cosx.

因为

所以

从而

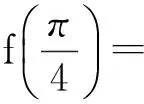
故选B.

点评解法1中利用基本不等式的性质求出其最小值，解法2中巧妙地利用原式取得最大值时sinx与cosx相等.

例5设a,b,c为三角形的3条边长，则

a2b(a-b)+b2c(b-c)+c2a(c-a)

的最小值为______.

解法1不妨设a≥b,a≥c，则

(1)当a≥b≥c时，

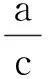
从而

a2b(a-b)+b2c(b-c)+c2a(c-a)≥

c2[a2b(a-b)+b2c(b-c)+c2a(c-a)]≥0.

(2)当a>c≥b时，

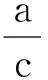
从而 a2b(a-b)+b2c(b-c)+c2a(c-a)≥0.

综合(1)，(2)，可得

a2b(a-b)+b2c(b-c)+c2a(c-a)≥0,

即a2b(a-b)+b2c(b-c)+c2a(c-a)的最小值为0.

解法2由题意可知，a,b,c是轮换对称，可知取最小值只会在三者相等时取到，即a=b=c，此时三角形为正三角形，故原式的最小值为0+0+0=0.

点评解法1中利用分类讨论的思想求出其最小值，解法2中巧妙地利用原式取得最小值时必为特殊的三角形(正三角形)，此时a=b=c.