几道高考题背后的圆锥曲线性质

●李金兴 ●胡名翔

(萧山中学 浙江萧山 311201) (复旦大学 上海 200433)

几道高考题背后的圆锥曲线性质

●李金兴 ●胡名翔

(萧山中学 浙江萧山 311201) (复旦大学 上海 200433)

1 从2000年的一道春季高考题说起

2000年普通高校春季招生考试(北京、安徽卷)第22题如下：

如图1，设点A，B为抛物线y2=4px(p>0)上原点以外的2个动点，已知OA⊥OB,OM⊥AB，求点M的轨迹方程，并说明它表示什么曲线.

因为当OA⊥OB时，直线AB过定点R(4p,0)，所以点M在以线段OR为直径的圆上，即点M的轨迹方程为x2+y2-4px=0(x≠0)，它表示的曲线是圆(去掉原点).点M是定点O在Rt△AOB斜边AB上的射影，不妨把点M的轨迹所在的圆x2+y2-4px=0称为“点O相对于抛物线y2=4px的射影圆”.

本文中，我们作如下定义：以定点P为直角顶点任作一个直角三角形，使斜边的2个端点A,B都在某一圆锥曲线C上，那么定点P在直线AB上的射影M总在一个定圆C′上，称定圆C′为定点P相对于曲线C的射影圆.

2 一类显而易见的推广

因为过圆锥曲线上一定点作2条互相垂直的弦，联结另2个端点的直线过定点，所以圆锥曲线上的任意一点都有相对于该圆锥曲线的射影圆.

例如，过抛物线y2=2px上一定点P(x0,y0)作2条互相垂直的弦PA,PB，则直线AB过定点R(x0+2p,-y0)(证明略).此时，点P在Rt△APB斜边AB上的射影M的轨迹在以线段PR为直径的圆上，该圆恰是“点P相对于抛物线y2=2px的射影圆”(如图2).类似地，在椭圆与双曲线中也有这样的结论(如图3和图4).

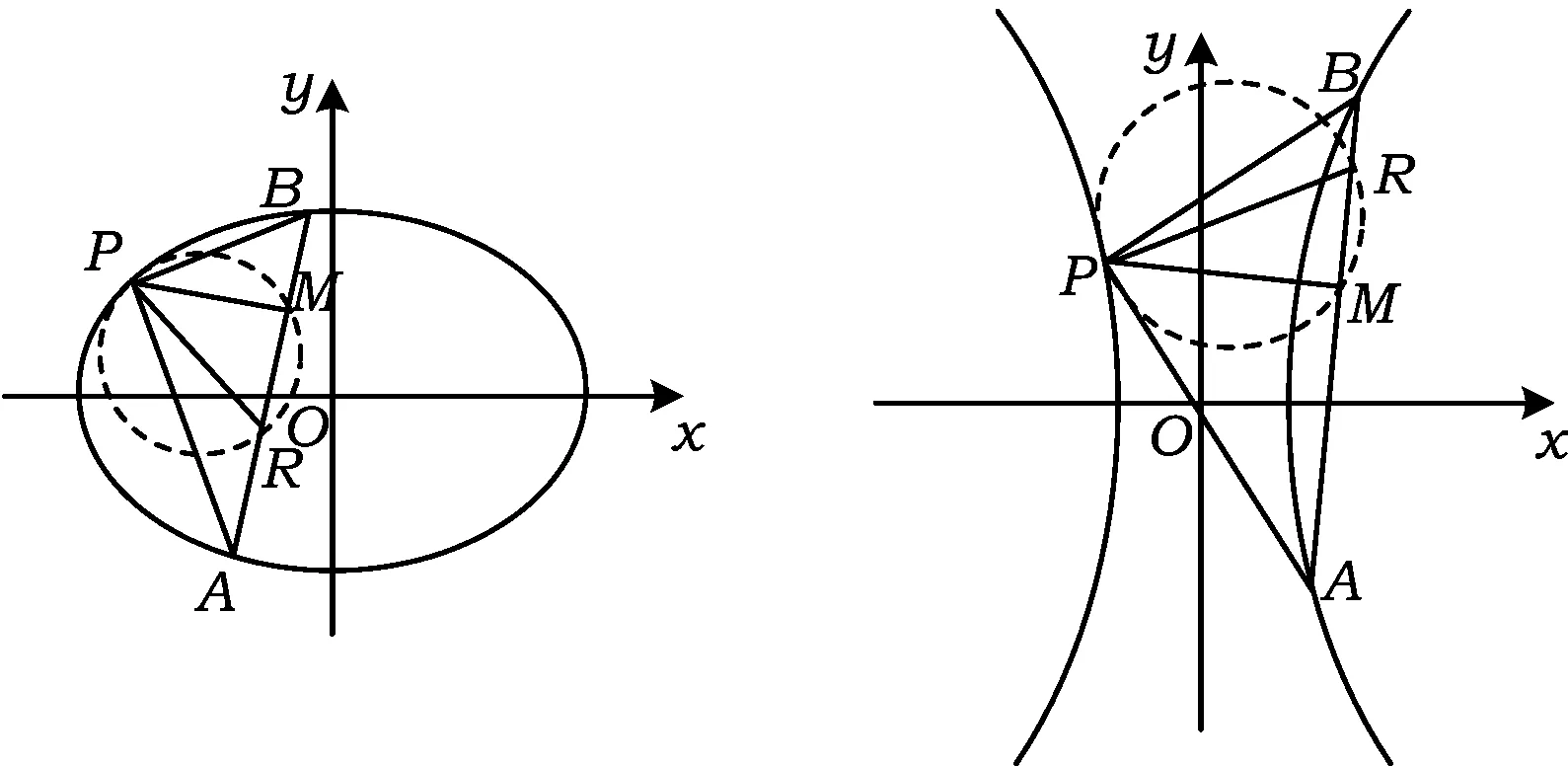
图3 图4

3 浅尝辄止的2009年高考题

2009年山东省数学高考理科第22题如下：

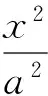
(1)求椭圆E的方程.

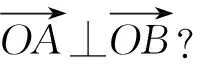
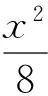
换个角度看(如图5)：以椭圆中心O为直角顶点作Rt△AOB，使得点A,B在椭圆上，则点O在斜边AB上的射影M的轨迹恰为一个圆(即点O相对于椭圆E的射影圆).

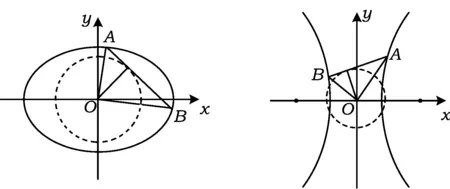
图5 图6

无独有偶，2009年北京市数学高考理科第19题如下:

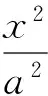
(1)求双曲线C的方程；

(2)设直线l是圆O:x2+y2=2上动点P(x0,y0)(x0y0≠0)处的切线，l与双曲线C交于不同的2个点A,B，证明:∠AOB的大小为定值.

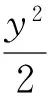
换个角度看(如图6)：以双曲线中心O为直角顶点作Rt△AOB，使得点A,B在双曲线上，则点O在斜边AB上的射影M的轨迹恰为一个圆(即点O关于双曲线C的射影圆).

4 定点相对于圆锥曲线的射影圆结论的进一步推广

综上可知，当定点在某圆锥曲线上或有心圆锥曲线的中心位置时，定点相对于该圆锥曲线的射影圆存在.那么，对于某圆锥曲线所在平面内的任意一定点，只要经过该点能作2条互相垂直的直线都与圆锥曲线相交，是否都有该定点相对于此圆锥曲线的射影圆存在呢？通过几何画板作图观察发现，结论是肯定的.

如图7，当点P不在抛物线上时，点P相对于抛物线的射影圆存在(图中虚线所示).

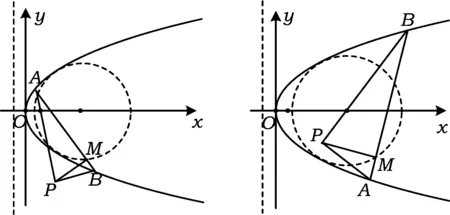
图7

如图8、图9、图10所示：对于圆、椭圆、双曲线，结论也成立.

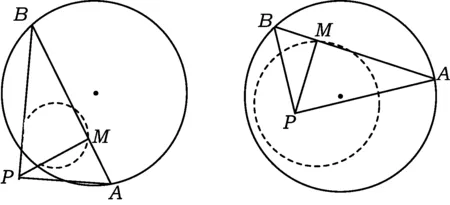
图8

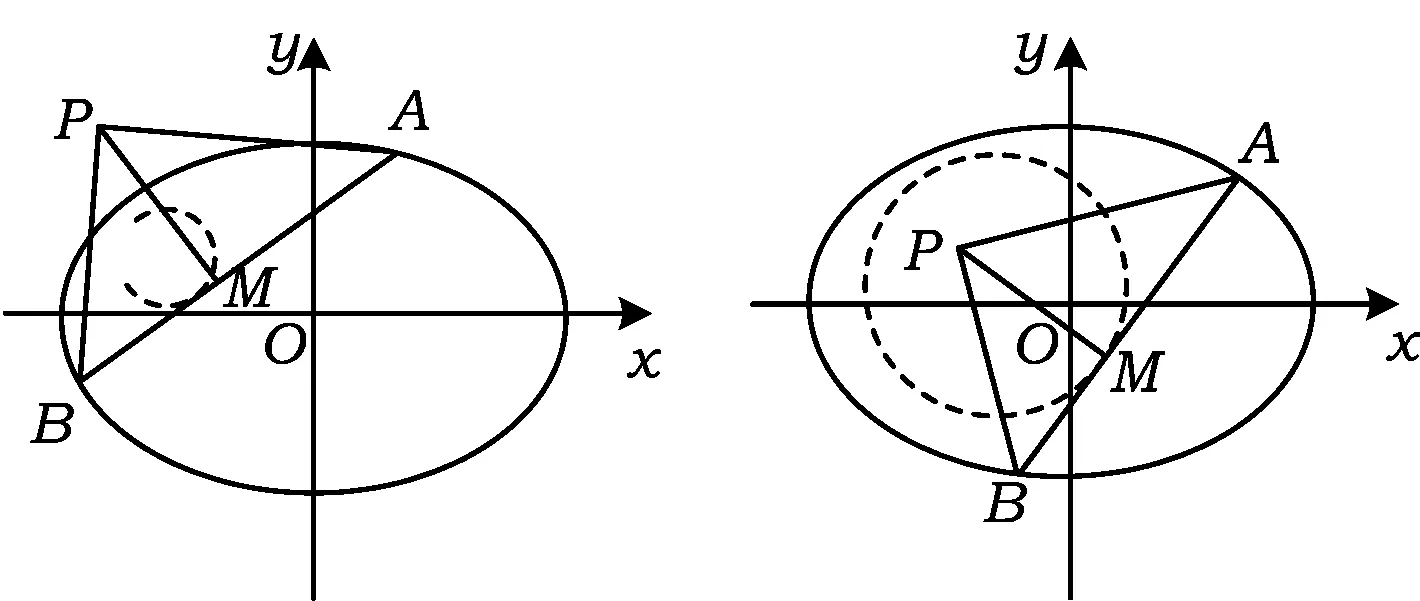
图9

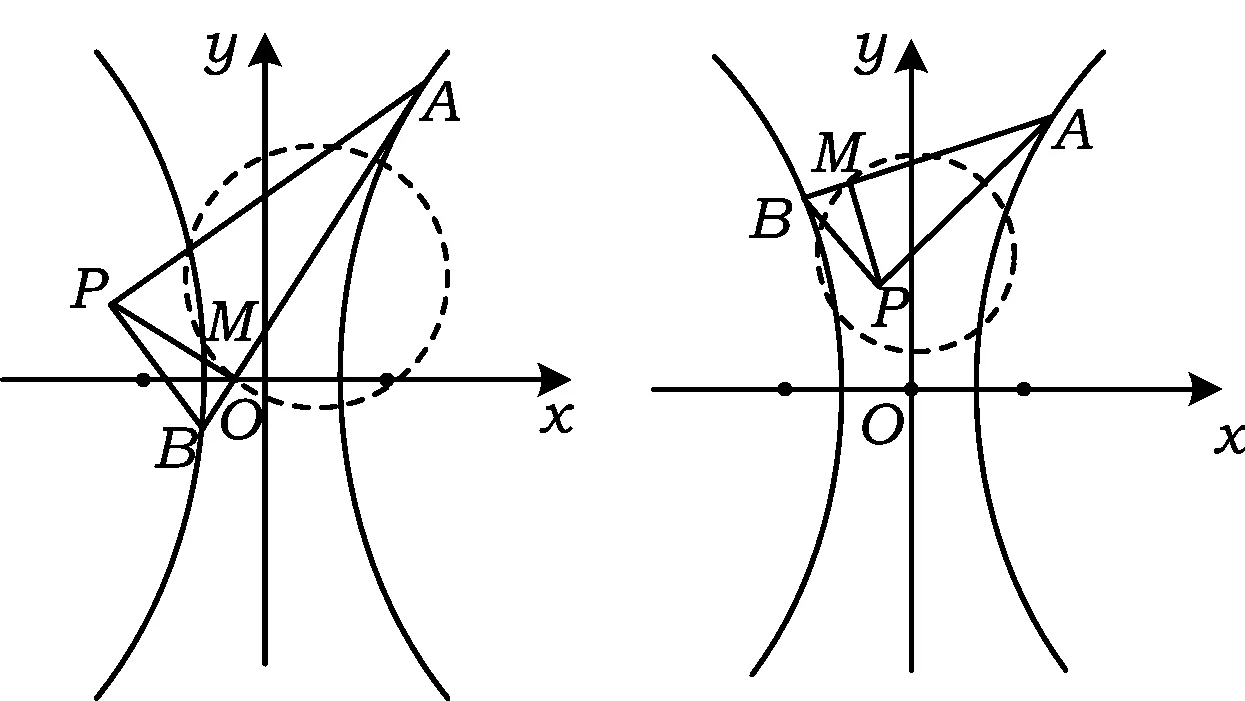
图10

5 定点相对于圆锥曲线的射影圆存在性的证明

可将推广后的结论归纳为如下问题：已知平面内圆锥曲线C和定点P，动点A,B在曲线C上且∠APB=90°，求证：点P在直线AB上的射影M总在一个定圆上.

证明分“点P不在曲线C上”和“点P在曲线C上”这2种情况讨论.

情况1当点P不在曲线C上时，以点P为原点适当建立坐标系，因为曲线C不过原点，所以圆锥曲线C的方程可化为

同理，因为直线AB不过原点，所以直线AB的方程可设为

此时，直线PM方程为

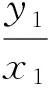
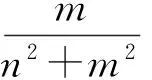
联立式(1)，式(2)并化为齐次式得

ax2+by2+(cx+dy)(mx+ny)=(mx+ny)2,

即 (b+dn-n2)y2+ (cn+dm-2mn)xy+

(a+cm-m2)x2=0.

(4)

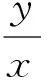
(b+dn-n2)k2+ (cn+dm-2mn)k+

(a+cm-m2)=0,

而k1,k2恰为上式方程的2个根,因此

b+dn-n2≠0且Δ>0.

由韦达定理知

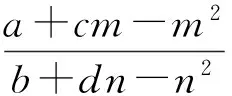
即

a+b+cm+dn=m2+n2,

于是

即

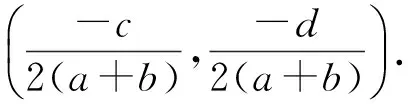
需要补充的是:若a+b=0,此时二次曲线为等轴双曲线,射影圆褪化成直线cx+dy=1.

(2)若x=0,则点A,B必在坐标轴上，得

可以验证此时点M也在上述圆(a+b)x2+(a+b)y2+cx+dy=1上.

需要补充的是：如果圆锥曲线与x轴或y轴无公共点，则点A或点B不存在，点M也不存在.

情况2当点P在曲线C上时，同样以点P为原点建立适当的坐标系，则圆锥曲线C过原点，方程可化为ax2+by2+cx+dy=0.直线AB的方程仍可设为mx+ny=1,则

ax2+by2+(cx+dy)·(mx+ny)=(mx+ny)2.

仿情况1可求得点M的坐标,使得

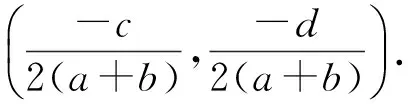
需要补充的是:若a+b=0,此时二次曲线为等轴双曲线,射影圆褪化成直线cx+dy=0.

6 对结论的反思反思1

在某些情况下，绕定点P旋转的2条互相垂直的直线只在一定区域内转动才能都与圆锥曲线相交，对应的射影M的轨迹只是射影圆的部分弧段(如图8和图9中的左图).

反思2当a+b≠0，c,d不都为0时，方程

(a+b)x2+(a+b)y2+cx+dy=0

表示圆，而当a+b≠0，c=d=0时，方程

(a+b)x2+(a+b)y2+cx+dy=0

仅表示坐标原点(无射影圆).事实上,当c=d=0时，圆锥曲线C的方程可化为ax2+by2=1，点P只能是有心圆锥曲线的中心,即原点.

反思3通常情况下，圆锥曲线的方程以“标准方程”的形式给出，而点P不在原点，此时，射影圆的方程可以利用坐标变换来解决.

例如，求抛物线C:y2=2px上点P(x0,y0)相对于抛物线C的射影圆.

由直线AB过定点R(x0+2p,-y0)的结论知，射影圆圆心为(x0+p,0).而以P(x0,y0)为原点建立新坐标系x′Oy′，则在新坐标系下，抛物线方程为

(y′+y0)2=2p(x′+x0)，

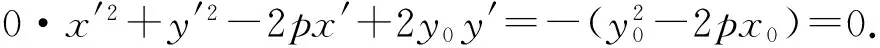
与方程ax2+by2+cx+dy=0相比，得

a=0,b=1，c=-2p，d=2y0,

[1] 胡典顺，徐汉文.一种新思路探求一类定点问题[J].中学教研(数学)，2007(10)：28-29.

文献[1]中“化齐次”的思想方法，该问题可得以巧妙地证明.