具有种群Logistic增长及饱和增长率SIR传染病模型的稳定性

宫兆刚，杨 柳

具有种群Logistic增长及饱和增长率SIR传染病模型的稳定性

*宫兆刚，杨 柳

（衡阳师范学院数学与计算科学系，湖南，衡阳 421008）

研究一类具有种群Logistic增长及饱和增长率SIR传染病模型，应用微分方程定性理论，分别得到了该系统的无病平衡点、地方平衡点全局渐近稳定的充分条件，并进行了数值模拟。

传染病模型；Logistic；平衡点；全局稳定性

0 引言

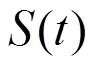
与

在这两类模型中分别讨论了标准发生率和双线性发生率的传染病模型，从传染病传播规律看，饱和增长率更符合实际，研究饱和增长率的传染病模型更有利于提供有力的保护措施，从而预测疾病的进展情况。

本文在研究了上述文献的基础上，研究了具有种群Logistic增长及饱和增长率SIR（Susceptibles Infectives Removed）传染病模型：

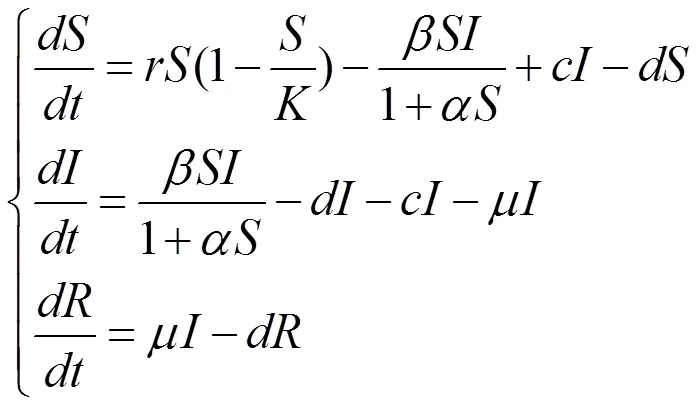
分析可知系统(1)的前两个方程不依赖第三个方程，因此仅考虑由系统(1)的前两个方程所构成的系统：

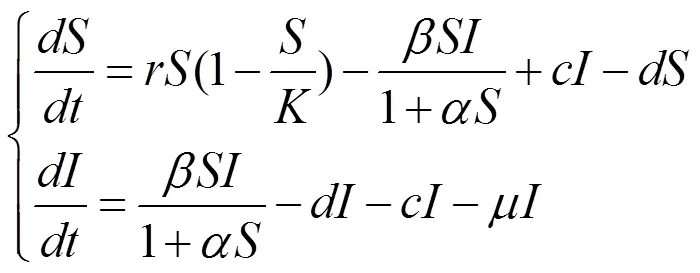
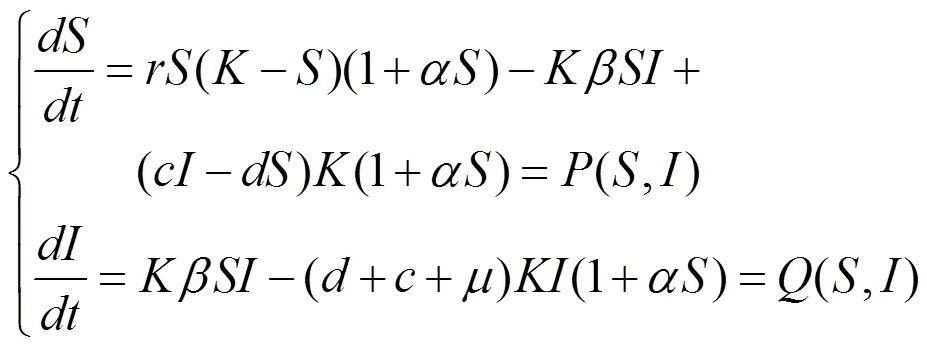
2 平衡点的存在性

解方程组

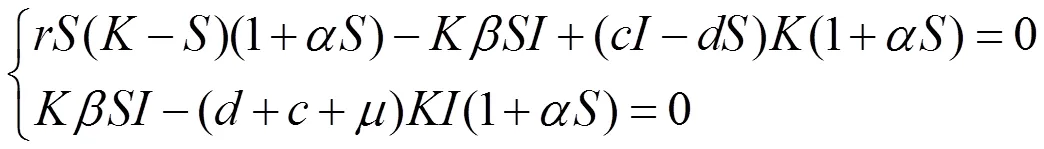
3 平衡点的稳定性分析

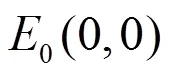
定理1 系统(3)的一切正解最终有界。

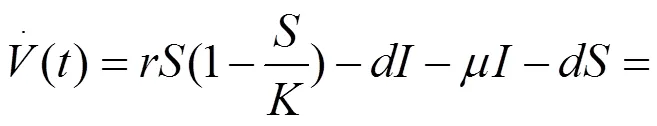
所以

因此系统(3)一切正解最终有界。

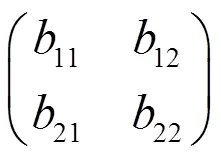
其中

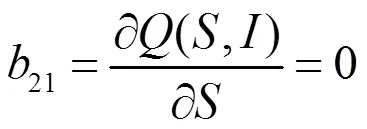
系统对应的特征方程为：

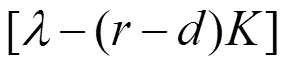
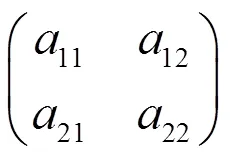
其中

即

其中

由上可得，系统(3) 在

所以由Bendixson-Dulac判别法，系统（2）在区域G内不存在闭轨线。

4 数值模拟

在这一部分我们给出了传染病模型的数值模拟，并从图1、图2中可以直观地看到上述证明的结论。

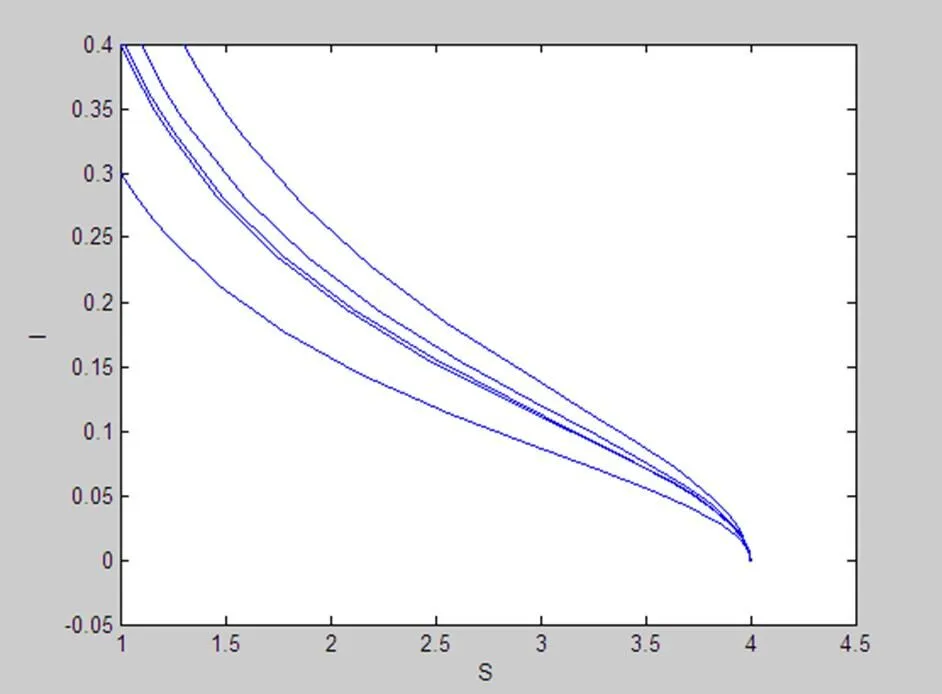
图1 无病平衡点1的数值模拟

Fig.1 The disease-free equilibrium1found by numerical simulation

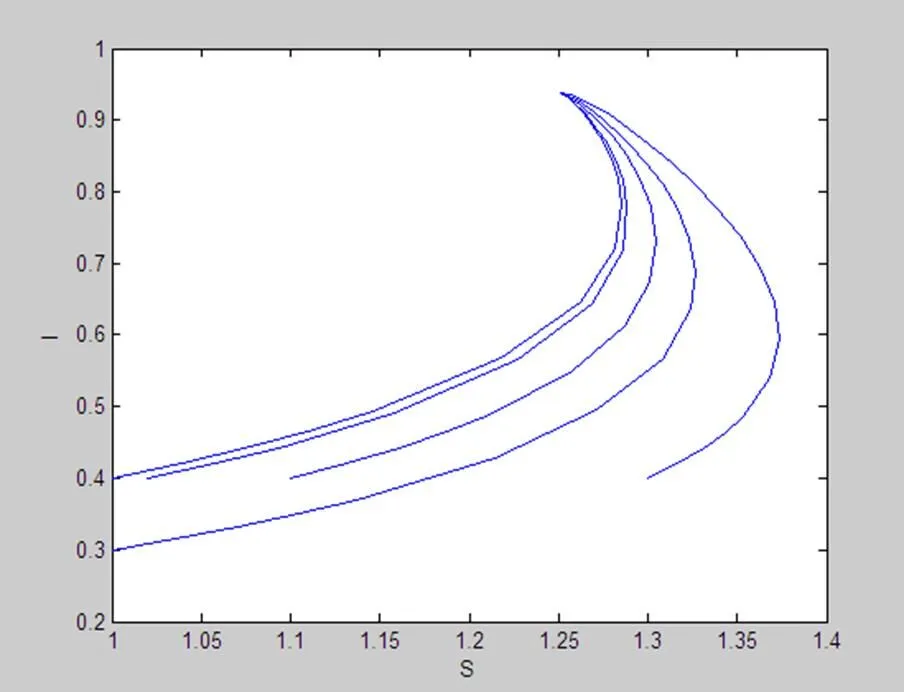
图2 地方病平衡点E2的数值模拟

[1] Karnack W O, McKendrick A G. Contribution to the mathematical theory of epidemic[J].Proc Kroc Roy Soc,1943,138(1):55-83.

[2] Li J,Ma Z.Qualitative analyses of SIS epidemic model with vaccination varying total population size [J]. Mathematical and Computer Modelling,2002,35: 1235-1243.

[3] 金瑜,张勇，王稳定.一类具有阶段结构的传染病模型[J].西南师范大学学报,2003,28(6):863-868.

[4] 程晓云,胡志兴.一类具有阶段结构的自治传染病模型的稳定性[J].石家庄学院学报,2007,9(3):23-27.

[5] 李建全,马知恩.一类带有接种的流行模型的全局稳定性[J].数学物理学报,2006,26(1):21-30.

[6] 原存德,胡宝安.具有阶段结构的SI传染病模型[J].应用数学学报,2002，25(2):193-203.

[7] 陈兰荪,陈键. 非线性生物动力系统[M].北京：科学出版社,1993: 111-123.

[8] 徐为坚.具有种群Logistic 增长饱和传染率的SIS模型的稳定性和Hopf分支[J].数学物理报,2008,28A(3): 578-584.

[9] 胡志兴,王辉,管可英.具有非线性接触率和时滞的SIRS流行病模型[J].应用数学学报,1999，22(1): 10-16.

[10] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

[11] 宫兆刚,蔡江涛,阳志锋.一类具有种群Logistic 增长的SIR 传染病模型的稳定性[J].贵州师范大学学报，2012,30(1):64-69.

[12] 宫兆刚,阳志锋.一类具有双线性发生率的SIS 传染病模型的稳定性[J].井冈山大学学报:自然科学版，2011,32(6):16-18.

GLOBAL STABILITY OF AN SIR EPIDEMIC MODEL WITH SPECIES LOGISTIC GROWTH AND SATURATING INFECT RATE

*GONG Zhao-gang YANG liu

(Department of Mathematics and Computing Sciences, Hengyang Normal University, Hengyang Hunan 421008, China)

An SIR epidemic model with species logistic growth and Saturating Infect Rate is investigated. By using the qualitative theory of ordinary differential equations, sufficient conditions are obtained for the global asymptotic stability of each of feasible equilibrium to the proposed model. Furthermore, some numerical simulations are provided to confirm our analytic results.

epidemic model; Logistic; equilibrium; global stability

O221.2

A

10.3969/j.issn.1674-8085.2013.03.004

1674-8085(2013)03-0013-05

2012-07-13；

2013-01-10

衡阳市科技局计划项目（2012KS15）；湖南省自然科学基金项目（12JJ9001）；湖南省科技计划项目（2012SK3117）；湖南省“十二五”重点建设学科资助项目

*宫兆刚(1978-)，男，吉林集安人，讲师，硕士，主要从事生物数学研究(E-mail:gzgfeixue781019@163.com)；

杨 柳(1971-)，男，安徽淮北人，副教授，博士，主要从事分数阶微分方程的研究(E-mail:yangliu19731974@yahoo.com.cn).