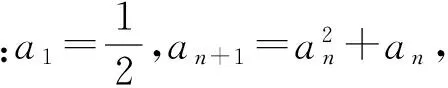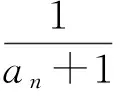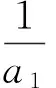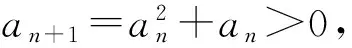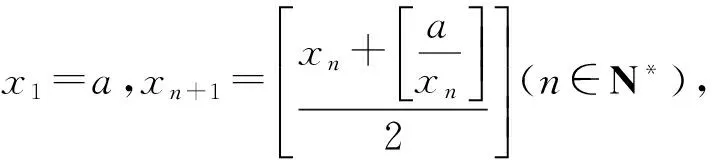活跃在高中的高斯函数
●
(浬浦中学 浙江诸暨 311824)
活跃在高中的高斯函数
●蔡明
(浬浦中学 浙江诸暨 311824)
近几年的数学高考以高等数学中的一些知识为背景进行考查,越来越受到大家的青睐.课外适当了解一些与初、高等数学相关知识的信息,对复习备考大有裨益,与眼下高观点的数学教学相吻合.下面以数论中的一个特殊函数——高斯函数为例,与大家一起探讨.
1 知识脉络
1.1 定义
高斯函数,也叫取整函数,设x∈R,用[x]表示不超过x的最大整数(如[-1.5]=-2,[1.5]=1,[2]=2),则函数f(x)=[x]叫做高斯函数.
1.2 性质
(1)函数f(x)=[x]的定义域为R,值域为Z;
(2)对任意实数x∈R,都有[x]≤x<[x]+1,也即x-1<[x]≤x;
(3)对于对任意实数x∈R,k∈Z,都有[x+k]=[x]+k.
事实上,在高中教材中已有高斯函数的习题(人教A版《数学(必修1)》习题1.2B组第3题).纵观近几年数学高考试题,源于课本的背景、例题、习题也屡见不鲜.查阅近几年的数学高考、会考以及各地模拟卷,在高斯函数的命题上主要以上述3条性质为主,并结合其他相关知识考查.
2 试题赏析
2.1 与函数结合考查
例1某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于6时再增选一名代表.那么各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]可以表示为
( )

(2010年陕西省数学高考试题)
分析本题的关键是取整问题的处理,可考虑采用特殊值法解选择题.
解法1(特殊取值法)若x=56,y=5,排除选项C,D;若x=57,y=6,排除选项A.故选B.
解法2设x=10m+α(0≤α≤9),当0≤α≤6时,
当6<α≤9时,
故选B.
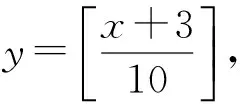
点评本题围绕取整函数的解析式进行处理,将所求问题转化成数,得到取整条件.
2.2 与不等式结合考查
例2[x]表示不超过x的最大整数,设集合A={(x,y)|x2+y2≤1},集合B={(x,y)|[x]2+[y]2≤1},则集合A∪B所表示的平面区域的面积等于______.
(2013年浙江省数学会考试题)
分析本题的关键是将[x]2+[y]2≤1转化成x,y的关系,根据高斯函数的值域为整数集,易实现转化.
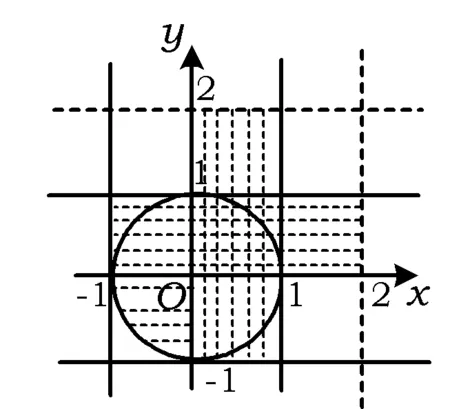
图1
解由于[x],[y]的值为整数,结合不等式可知
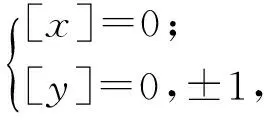
结合高斯函数性质(2)可得
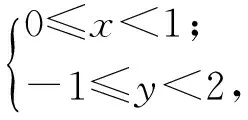
点评准确利用值域为整数集的性质,将取整函数问题转化为一般可行区域进行处理,达到“柳暗花明又一村”之感.
2.3 与方程(组)结合考查

分析本题与常见方程组比较,出现不一样的量[x],[x-3],如能转化就可迎刃而解.
解由[x-3]=[x]-3,知原方程组变成

解得
[x]=20.
由于x不是整数,故20 点评本题的关键在于性质(3)的应用,达到归一思想. 2.4 与数列结合考查 ( ) A.是等差数列但不是等比数列 B.是等比数列但不是等差数列 C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列 (2009年湖北省数学高考试题) 分析本题中{x}=x-[x],即数的小数部分处理是重点. (2013年浙江省五校联考数学试题) 即 点评本题虽以高斯函数为背景,但真正考查在于其他知识的处理,体现醉翁之意不在酒. ①当a=5时,数列{xn}的前3项依次为5,3,2; ②对数列{xn}都存在正整数k,当n≥k时总有xn=xk; 其中真命题有______(写出所有真命题的编号). (2012年四川省数学高考试题) 分析结合本题的特殊性,可考虑使用特殊值法(a=1,2,3)处理,得①③④是真命题. 对③,由xn为整数,得 则 故③正确; 点评此题难度较大,不容易寻找解题的切入点,特殊值列举是很有效的解决办法. 从上述试题来看,与高斯函数相关的命题主要集中在函数与数列问题,同时可发现高斯函数以概念给出,其性质需要自己去挖掘,这也是将问题转化的一种手段.当然高中阶段所学的知识方法与能力,是解决这些问题的关键 .倘若能借助于高等数学知识去理解问题,则具有茅塞顿开的感觉,对处理问题有事半功倍之效.眼下实行深化新课改,教师可在适当时机运用选修课程的形式,冠以高等数学中与高中数学密切相关知识的学习,拓展学生的视野与能力.