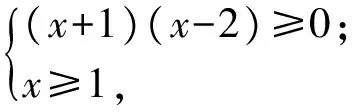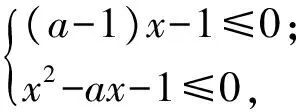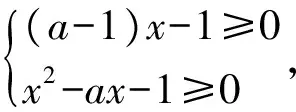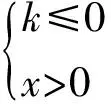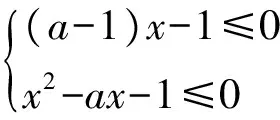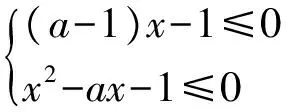一道不等式恒成立高考题的错解分析
●
(陕西师范大学数学与信息科学学院 陕西西安 710062)
一道不等式恒成立高考题的错解分析
●罗增儒
(陕西师范大学数学与信息科学学院 陕西西安 710062)
2012年浙江省数学高考理科第17题如下:
例1设a∈R,若x>0时均有[(a-1)x-1]·(x2-ax-1)≥0,则a=______.
这道试题出来后,立即以其形式的简单性、内容的新颖性、思维的灵活性与广阔性等特征引起关注,本刊曾连续发表文章加以研讨(见文献[1]~[4]),也有作者多次撰文连续研讨(见文献[5]~[6]).从见于各刊的部分文章(见文献[1]~[13])分析显示:作者对本例作为数学题的关注多于作为考试题的关注,对本例正面求解的关注多于纠错订正的关注.从对高中数学教师和高三学生的测试表明:
(1)难度系数很低.这道4分题在10分钟时间内的通过率不到0.2,属于考试中的低效题(可能与东西部的教育差异有关).另有文献[2]认为:这是学生熟悉的“恒成立”命题,但成功解题的人却不多.文献[13]认为:大部分学生感觉有困难.
(2)纠错力度不足.对于学生中的错解,不少教师看不透,归因不当或者逃避归因——直接给出正确解答了事(见文献[7]等).
鉴于此,笔者将本例作为解答题来研讨,并重在纠错,涉及3个方面的认识:
(1)在本例的处理中存在哪些主要的错解?(本文提到4个错解.)
(2)这些解法错在哪一步、错误的性质是什么?(主要有3类:知识性错误、逻辑性错误、心理性错误.)
(3)如何对错解直接订正?
至于本例的众多解法(有10余种:代数解法、几何解法、取特殊值解法等),限于本文的主题,不再赘述.
1 错解的呈现
1.1 错解1的呈现
由两式的乘积非负,则两式同时非正或同时非负,可将已知不等式等价于以下2种情况:
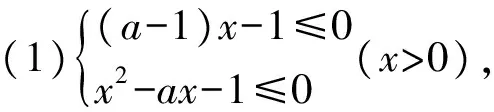
x2-x-2≤0,
即(x-2)(x+1)≤0对x>0恒成立.这是不可能的(取x=3,例1无解).

x2-x-2≥0,
即(x-2)(x+1)≥0对x>0恒成立.这是不可能的(取x=1,例1无解).
综合2种情况,例1无解(或是一道错题).
说明这是学生中的一种常见思路,文献[1],[2],[5]~[8],[12]都有所提及,如:
(1)文献[1]列出2种情况后,认为:受到经验的影响,很多学生认为本题可能是错题或者解不出.
(2)文献[6]以师生讨论的形式展现学生思路,认为:这不是解不等式,这是一个在x>0时的恒成立问题,学生1没有注意x>0而误认为是错题.文献[12]也认为:学生把f(x)g(x)≥0恒成立与解不等式f(x)g(x)≥0混淆了.(读者可能会疑惑:难道例1不是不等式问题?)
该文献认为:错误的原因是由于受到解题经验的影响,将不等式化为了恒不等式.(读者可能留下“2种情况导致解不出本题”的印象,分不清“解题经验”到底是积极的还是消极的.)
1.2 错解2的呈现
对a-1分2种情况讨论:
(1)当a-1≤0时,由x>0知
(a-1)x-1<0,
结合已知可得
x2-ax-1≤0,
从而
即
解得
0 解得 (2)当a-1>0时,由已知可得 即 从而 2a2-3a=0. 1.3 错解3的呈现 由[(a-1)x-1](x2-ax-1)≥0,特别地,取两式同时为0,得 从而 说明对于学生的这一思路,文献[2],[4]有类似的处理: 2.1 对错解1的辨析 2.1.1 错解1是“会而不对” 即分2种情况讨论确有合理成分(下面有合理性的说明),但它的“等价性”依据比较隐晦,所得出的“无解”结论是错误的,叫做“会而不对”. 2.1.2 错解1的错误内容(主要有3点) 错误1等价性的依据是含糊的,即由“两式的乘积非负,则两式同时非正或同时非负”推出“2种情况”,有一种令人“半信半疑”的含糊.还有“日常语言”与“数学语言”的歧义.因为在情况(1)中,当(a-1)x-1≤0时不能由[(a-1)x-1](x2-ax-1)≥0推出x2-ax-1≤0,仅当(a-1)x-1<0时,才能由已知推出x2-ax-1≤0;同样,在情况(2)中,仅当(a-1)x-1>0时,才能由已知推出x2-ax-1≥0.而当(a-1)x-1=0时,x2-ax-1可以小于0、等于0、大于0.请看一个例子: 从而 故 x≥2. 这说明“两式的乘积非负,则两式同时非正或同时非负”可能会由于含糊而产生歧义. [(a-1)x-1](x2-ax-1)≥0 可以保持不重不漏.其几何直观如图1和图2所示(图2中a记为y,参见解法4和解法5). 图1 图2 因此,我们说分2种情况讨论确有合理成分,其合理性可用集合语言更准确地表示为: {x|f(x)g(x)≥0}= 这时,例2可合理求解: {x|x≥2}∪{x|x=-1}. 错误2构成矛盾无效.其实,错解1分2种情况讨论的同时,也对x∈(0,+∞)分成了2种情况(见图2的阴影部分).对于第(1)种情况,有 即 从而 0 对于第(2)种情况,有 即 从而 x≥2. 因此,2种情况下构成矛盾都是盲目的、无效的. 换句话说,以下等价关系为真命题: 而下面的等价关系为假命题: 这就是学生错误的真正原因,也是许多文章没有正面点明(或有所逃避)的要害之处. 错误3心理沿袭和监控缺失.在分2种情况讨论的同时,也把x∈(0,+∞)分成x∈(0,2]与x∈[2,+∞)这2种情况,这在错解1中已有明显的暴露: 但是错解1对此视而不见,2种情况下都依然沿袭x可取(0,+∞),并由此出发去构成矛盾,这除有知识盲点、逻辑盲点外,还有视而不见的心理沿袭和反思监控的思维缺失. 另外,对于方程和不等式,“问题无解”并不等同于“错题”(可记为错误4). 2.1.3 错解1的错误性质 由上面的分析可见,错解1既有知识性错误,又有逻辑性错误,还有心理性错误,但主要是逻辑性错误.不去纠正错误是“误人子弟”,不从逻辑关系上去纠正错误是“隔靴搔痒”. 2.1.4 错解1的直接订正 正解1(代数法)由等价关系 {x|f(x)g(x)≥0}= 可以把已知不等式变为以下2种情况: 两式相加消去a,得 从而 0 得 两式相加消去a,得 从而 x≥2. 得 说明这样处理表明错解1可以完善,不应回避,但原理比较隐晦,书写比较曲折,其简化处理可为: 正解2(代数法)更换主元,将已知式看成关于a的不等式,对x>0有 (1)当0 得 (2)当x≥2时,解关于a的不等式(1),得 得 说明正解2显然比正解1原理较为显浅,讨论更为自然,书写更简洁,但内容实质却是一样的: 正解2的几何意义见图1和图2,及解法4和解法5. 2.2 对错解2的辨析 2.2.1 错解2是“对而不全” 2.2.2 错解2的错误内容 主要针对a-1≤0的情况说明3点: 2.2.3 错解2的错误性质 由上面的分析可见,错误1是知识性错误,错误2是逻辑性错误,错误3是心理性错误. 2.2.4 错解2的直接订正 正解3(代数法)分2种情况讨论. (1)当a-1≤0时,有2a-3≠0,取x=2>0,得 [(a-1)x-1](x2-ax-1)=-(2a-3)3<0, 这说明不大于1的a不满足条件,此时无解. 说明这样处理是对错解2的完善,它的几何解释如下.当a>1时,三次函数 有“一负两正”3个零点(如图3),要使x>0时f(x)≥0恒成立,当且仅当2个正根重合为切点(如图4). 图3 图4 2.3 2个错解的对比分析 学生的2个错解:一个“会而不对”;一个“对而不全”,都已讨论清楚,现在把2种错解及其订正都回顾一下,大家可以看到这样的对比: 表1 错解1和错解2的比较 图5 图6 2.4 对错解3的辨析 2.4.1 错解3是“对而不全” 2.4.2 错解3的错误内容 问题1“特别地”使人感到好像是一个必要条件过程,如果是必要条件,那就还缺少充分性的验证. 问题2设y1=(a-1)x-1,y2=x2-ax-1.则y1y2≥0可以分解为7种情况(参见图2中的阴影部分): “取两式同时为0”只是其中一种情况,从这一意义上说,“特别地”又像是一个充分条件.而充分条件则存在减根的危险. 当然,如果有唯一性作保证,那么,“特别地”取两式同时为0是可以的,问题是,由题目求“a=______”能否断定a是唯一确定的值呢?我们说不能,a也可以取不只一个值.比如 2.4.3 错解3的错误性质 由上面的分析可见,2个错误内容都属于逻辑性错误. 2.4.4 错解3的直接订正 正解4(数形结合)如图1,作出函数y=(a-1)x-1(直线)和y=x2-ax-1(抛物线)的图像,可知 (1)2个函数图像都过定点(0,-1). (2)在x>0的右半平面上,绕定点(0,-1)旋转直线y=(a-1)x-1可以看到,2个函数图像或者同时不在x轴下方、或者同时不在x轴上方,满足条件的图形只能是:2个函数图像的另一交点在x轴上.即[(a-1)x-1](x2-ax-1)≥0对x>0恒成立的的充要条件是 从而 说明这里有一个双流向的“数形结合”,首先是“式子—函数—图像”一步步“由数到形”,等把图形看清楚了、想明白了,再“图形特征—函数性质—方程求解”一步步“由形到数”,是双流向的“数形结合”.这个解法的成功基于图像特征的洞察,关键是发现:2个函数图像或者同时不在x轴上方、或者同时不在x轴下方,从而三线共点. 的区域为图2中的阴影部分,当且仅当水平直线通过2个图像的交点时(三线共点),整条射线(x>0)均落在阴影区域上.即[(a-1)x-1](x2-ax-1)≥0对x>0恒成立的充要条件是 从而 说明这里的双流向“数形结合”与正解4略有区别,首先是“式子—曲线—区域”一步步“由数到形”,然后是“图形特征—区域性质—方程求解”一步步“由形到数”.如果说正解4的图像需要作较多动态理解的话,那么,正解5的区域是较为静态的. 以上个人看法,盼同行们批评指正,最后,留一道练习题供自我检验. 练习题请分析本例的下述解法是否正确?如有错误,错在哪里?错误的性质是什么?如何订正? 解由[(a-1)x-1](x2-ax-1)≥0,得 x2a2-x2(x+1)a+(x+1)2(x-1)≤0. 令f(a)=x2a2-x2(x+1)a+(x+1)2(x-1),因为当x>0时,x2>0,所以关于a的一元二次函数开口向上.要使在参数x>0的情况下均有f(a)≤0,只能是f(a)=0,因此判别式Δ=0,即 x2(x+1)2(x-2)2=0. [1] 陆立峰.四法并举 彰显活力[J].中学教研(数学),2012(8):39-41. [2] 孙海琴.不畏浮云遮望眼 深思熟虑子自如——2012年浙江省数学高考解题追踪调查研究[J].中学教研(数学),2012(12):37-39. [3] 林怀传.接天莲叶无穷碧 映日荷花别样红——2012年浙江省数学高考创新题评析[J].中学教研(数学),2012(8):15-17. [4] 黄超.挖掘数学思想探究数学本质——2012年浙江省数学高考函数问题评析[J].中学教研(数学),2013(1):42-45. [5] 王剑明.继承与创新同在传统与开放并存——2012年浙江省数学高考理科第17题赏析[J].中学数学:高中版,2013(1):95-97. [6] 王剑明.探究演绎精彩,互动彰显魅力——2012年浙江省数学高考理科第17题课堂探究实录与思考[J].数学教学通讯,2013(4):26-27. [7] 王朝璇.容易“碰壁”的高考题三例[J].中学生数学:高中版,2013(1):40-41. [8] 魏定波.一道内涵丰富的创新试题[J].中学数学研究,2012(10):38-39. [9] 王勇,李燃.点击2012年高考数学中的图像试题[J].中学数学杂志,2012(11):42-46. [10] 张金良.关于高中数学试题评价标准的探索[J].中国数学教育,2013(1/2):76-78. [11] 郑日波,沈新,蒋荣清.平淡中见灵动 细微处显意蕴——2012年浙江省高考数学试卷评析[J].数学通报,2013(2):17-19. [12] 沈志刚.通法难得正确?——几类含参恒成立问题的通法困惑及其求解策略[J].数学通讯,2013(4):27-28. [13] 谢旭初,阮伟强.答案对了够不够[J].中学数学研究,2013(4):43-45. [14] 罗增儒.与“国培”学员一起做“错例分析”——一道不等式恒成立高考题的深度交流[J].中学数学教学参考,2013(5):2-5.

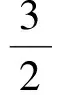



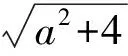
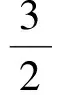



2 错解的辨析