考虑环境效益的城市快速路匝道协调控制

胡灵龙， 王绍楠， 孙伟力， 王 慧

(浙江大学控制科学与工程学系，浙江杭州310027)

城市快速路交通拥堵问题已成为全球各大城市面临的共同问题。入口匝道控制是缓解和预防交通拥挤的一种有效控制方式，通过限制进入快速路的车辆数目使得快速路网上的交通流量趋近合理状态，它在国内外已经得到广泛应用［1］。

快速路匝道控制策略可分为单点控制和协调控制。经典的单匝道控制策略有需求-容量控制、占有率控制和ALINEA控制［1］;多匝道协调控制的研究包括非线性最优化控制［2］、双层规划模型优化［3］、阈值控制［4］、模型预测控制［5］等。其中匝道模型预测控制(Model Predictive Control，MPC)作为当前研究前沿，具有良好的应用前景。但是，上述匝道控制的策略研究基本上都是以缓解交通拥堵为首要目标，很少考虑环境效益，如机动车尾气排放问题。

随着城市机动车尾气污染问题的不断加剧，道路交通环境问题日益突出。作为城市大运载量的交通干道，快速路若发生交通拥堵现象会致使路面上大面积车辆频繁地启动、加速、减速和怠速，降低通行效率的同时进一步加剧交通污染状况。目前，对交通控制优化策略的环境效益进行建模和仿真评价的研究［6］已有不少，但是如何从控制角度上对其改善交通环境污染方面的研究较少。Zegoye S K等［7］把宏观动态交通流模型和国外研究成熟的污染物排放模型及燃油消耗模型相结合，为匝道最优控制能够兼顾通行效率和环境效益提供了一种基础模型。

文中从城市快速路交通流模型入手，以入口匝道模型预测控制为手段，兼顾道路通行效率和环境效益双重控制目标，探究解决城市快速路交通拥挤的匝道优化控制策略，并达到减少机动车尾气排放、改善城市交通环境的目的。

1 快速路系统MPC框架

针对城市快速路入口匝道系统，兼顾道路效率性能和环境效益指标，图1给出了文中匝道MPC调节方法的框架。

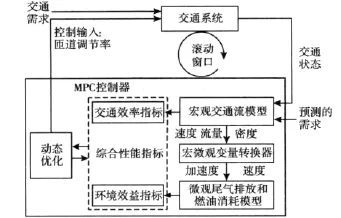
图1 匝道MPC调节框架Fig.1 Model predictive control framework

其基本原理如下:①在给定控制匝道序列作用下，采用一个快速路交通流模型预测路网交通变量的演化轨迹;②通过宏微观变量转换器，实现宏观交通流模型和微观尾气排放模型的结合，构建环境效益指标;③以交通效率和环境效益指标最优为目标函数，考虑输入与输出的实际约束，构造非线性动态最优控制模型;④在每一次滚动优化中，通过求解相应的优化命题得到最优匝道调节率序列，并将第一个控制量作用于交通系统;⑤在下一个滚动周期，控制器根据交通系统的当前数据更新系统状态(反馈性)，重新执行优化计算，以此循环。

2 控制优化命题构建

2.1 宏观动态交通流模型

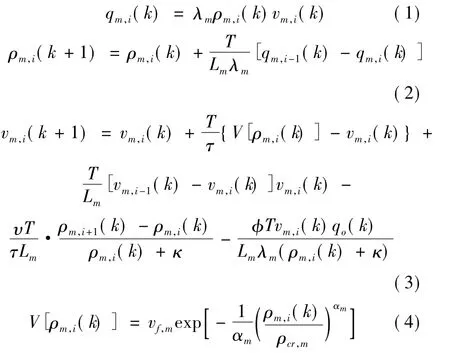
采用二阶宏观动态交通流模型METANET描述快速路匝道控制系统［5］。该模型根据道路特性将路网分为若干道路m，每条道路又被分成Nm段，路段长度为Lm;采样周期为T，时间离散化为t=kT(k=0，1，…，K);道路m第 i路段在第 k采样时刻的流量、密度、平均速度依次记为 qm，i(k)，ρm，i(k)，vm，i(k)(i=0，1，…，Nm)。以道路 m 路段 i为研究对象，建立如下快速路主路路段动态模型:

其中，λm为路段的车道数;vf，m为自由流速度;ρcr，m为临界密度;αm为流-密基本图参数。τ，ν，κ 和 φ 为表征路网交通特性的参数。式(1)为交通流定义方程;式(2)表明车辆守恒原理;式(3)为经验速度方程，描述了路段平均速度的动态轨迹;式(4)描述了流量-密度基本图。

采用排队模型描述入口匝道与快速路衔接处模型。在时间段［kT，(k+1)T］内，定义以下变量:do(k)为入口匝道处需求量;qo(k)为实际从入口匝道汇入快速路的流量;ωo(k)为入口匝道处车辆的排队长度。ro(k)∈［0，1］为入口匝道控制率。排队模型由下式描述:

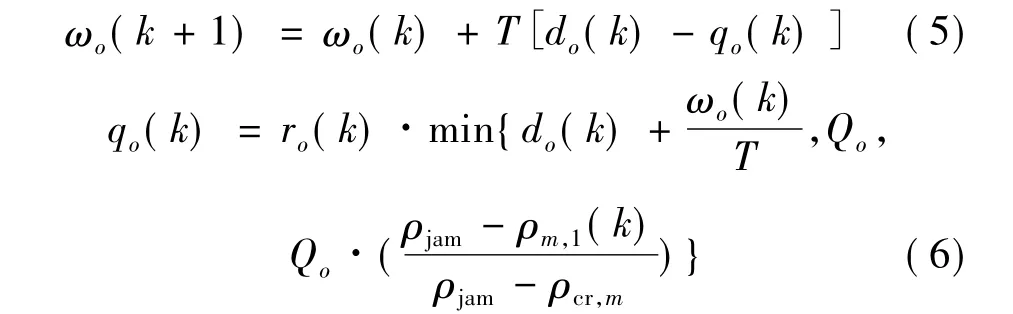
式中，Qo为入口匝道最大汇入流量;ρjam为阻塞密度。常用的性能指标为路网总耗费时间，包括快速路上车辆在系统中消耗的行驶时间和入口匝道车辆排队等待时间。其表达式为

2.2 环境效益指标建模

文中采用宏观交通流模型与微观排放模型集成方法，把宏观交通流模型中的宏观变量，换算成微观尾气排放模型所需的瞬时加速度、速度和对应的车辆数。

在METANET模型中，对于道路m第i路段上在第k时刻的车辆，其瞬时速度v即可由平均速度vm，i(k)代替，而加速度a和相应的车辆数n通过速度变量计算。定义快速路路段上车辆在下周期维持在本路段的加速度为时间加速度at，而进入下一路段的加速度为时空加速度as，nt，ns分别为两类加速度所对应的车辆数。入口匝道处车辆的加速度和对应的车辆数记为aon和non。3种加速度和对应车辆数的计算表达式如下:

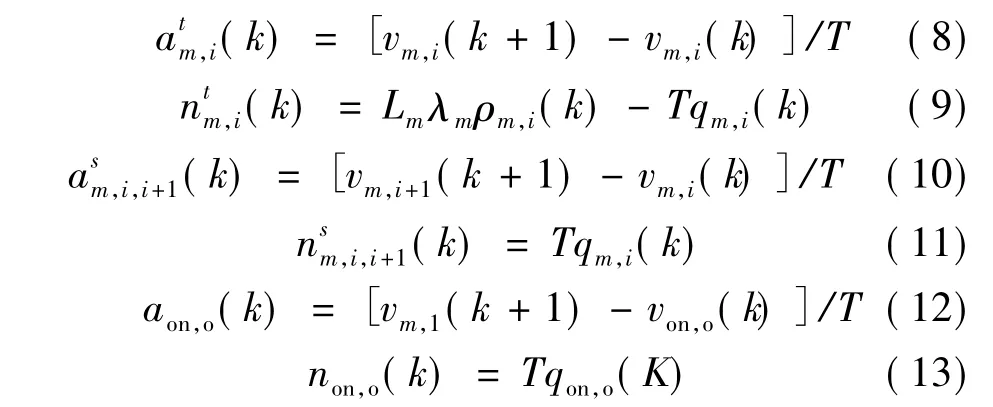
式(12)中 von，o为匝道上的车辆速度。根据Greenshields模型得出;式(13)中 qon，o即为式(6)得出的实际入口匝道流量。

VT-Micro模型［7］反映了机动车速度、加速度和尾气排放、燃油消耗的关系。结合上述得到的机动车速度、加速度和车辆数，即可得到VT-Micro模型新的计算表达式。以时间加速度为例，道路m第i路段在kT时刻的机动车燃油消耗或排放量为

其中，下标 y∈ {CO，HC，NOx，FC}，FC 为燃油消耗(Fuel consumption)的简称。Py为参数矩阵，文中参考文献［8］的取值。另两种加速度情况的指标计算形式类同。路网中机动车尾气的总排放量和总燃油消耗量为

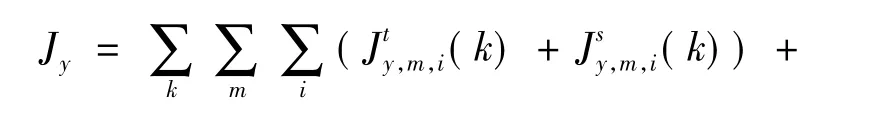
2.3 动态非线性最优控制

每一次滚动优化，都可将最优控制序列的求解转化为带控制变量约束的离散时间动态非线性最优控制问题。将快速路视为控制过程，该过程的状态描述为状态向量，输入变量分为控制变量和不可控的外部干扰。记k为模型采样时间坐标，对应采样周期T;kc为滚动优化时间坐标，对应控制周期Tc。一般地，取Tc为T的整数倍，即Tc=ZT(Z为正整数)，表示实际控制中决策变量更新周期(几十秒到几分钟)通常是交通流模型采样周期(10 s左右)的倍数。Np为模型预测时长，Nc为模型控制时长。每一次滚动优化的最优控制命题描述如下:

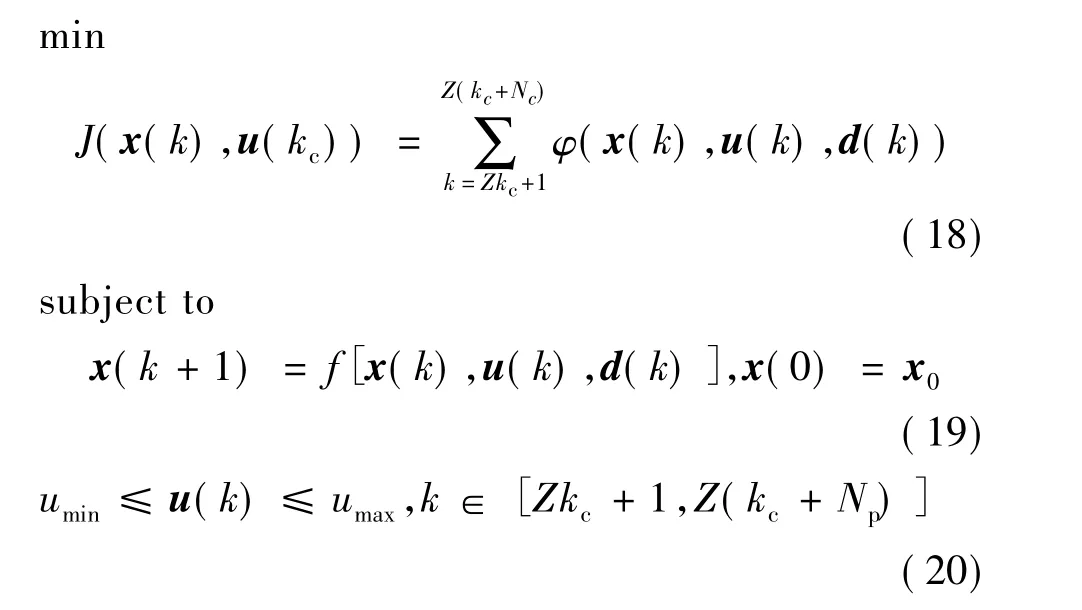
其中，状态向量 x 由基本路段的密度 ρm，i、速度 vm，i和入口匝道处的排队长度wo组成;控制向量u为匝道控制率 ro，并且存在约束 ro(k)∈［umin，umax］;干扰向量d由路网中入口路段的需求do组成。φ为目标函数，可在文中综合考虑式(7)的路网总耗费时间和式(17)的各项环境效益指标，并基于各指标在匝道不控制情况的数值作归一化处理［9］得到。

2.4 优化算法求解

采用离散系统的极小值原理［10］求解每一轮滚动优化的最优控制问题。离散Hamiltonian function函数和最优解需满足的必要条件如下:

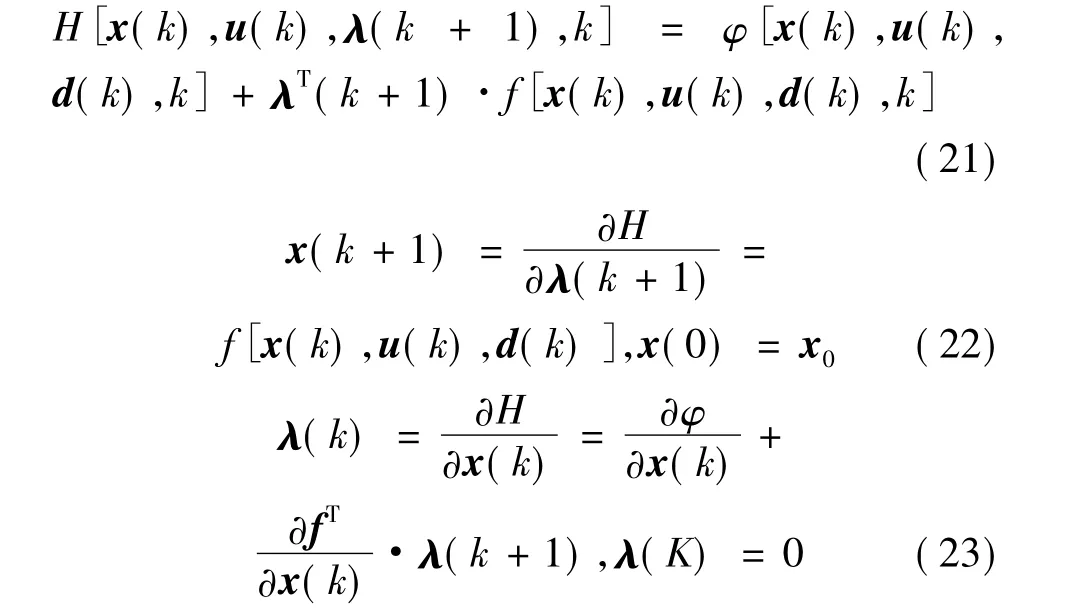
给定控制变量的可行解u(kc)后，根据式(22)可从初始状态x(0)求解得状态轨迹x(k+1)，因此目标函数可视为仅受控制变量的影响，即J=¯J(u)，具体形式为

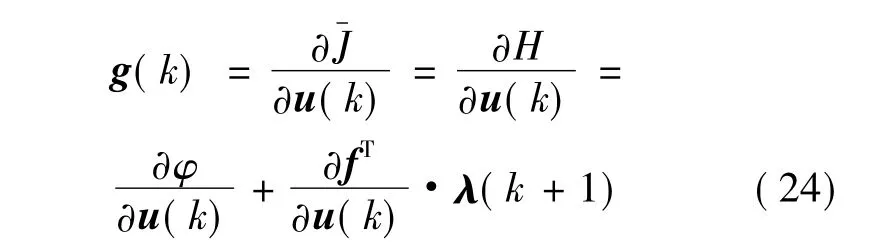
因为控制变量存在约束，定义梯度ξ(kc)作为g(kc)的修正形式，若控制变量在约束范围内，即满足式(20)，那么ξi(kc)等于gi(kc)，否则ξi(kc)=0。算法求解的具体步骤如下:

1)设置初始迭代次数ι=0，选择控制变量的初始可行解u(0)(kc);

2)根据当前状态变量x(ι)(kc)及给定的控制u(ι)，依据式(22)正向递推求得 x(ι)(Zkc+1)，x(ι)(Zkc+2)，…，x(ι)(Z(kc+Np));

3)依据式(23)逆向递推求得λ(ι)(Z(kc+Np)-1)，λ(ι)(Z(kc+Np)-2)，…，λ(ι)(Zkc+1);

4)对控制时长内的每一个kc，依据式(24)求得梯度 g(ι)(kc)及其修正形式 ξ(ι)(kc);

5)采用梯度法PROPO［2］求解出下一步的控制轨迹 u(ι+1)(kc);

6) 给定允许误差 σ，检验(Jι+1-Jι)/Jι＜ σ 是否满足，若满足则停止迭代，得到最优解;否则将迭代次数ι加1并返回2)。

在每一次滚动优化中，考虑到交通流变量演化的渐进性，选用当前周期的最优控制轨迹作为下一个周期的初始值，在一定程度上能够加快收敛速度。

3 仿真结果与分析

3.1 仿真场景设置

为验证文中提出的控制方法的有效性，对一虚拟路网进行仿真测试。

路网拓扑结构如图2所示。

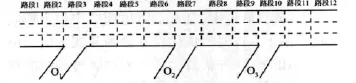
图2 路网拓扑结构Fig.2 Road network topology

路网包括一条三车道的快速路主路和汇入其中的三个单车道匝道。主路分为12个路段，每个路段长度为500 m，在第3，7，10个路段有入口匝道汇入。交通需求如图3所示。

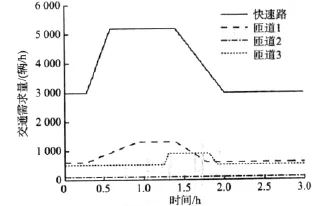
图3 路网交通需求量Fig.3 Demand scenario

图3模拟了一个快速路日常通行的高峰场景，其中1号、3号入口匝道同样有个小高峰现象，且1号匝道与主路的高峰时段同步，而3号匝道出现高峰的时刻晚于主路。该场景的设置源于对实际交通场景的简化处理，目的使此策略能为工程实践提供一定的理论依据。

路网参数设置见表1，使得主路及入口匝道的通行能力分别达到2 000辆/h/车道和1 500辆/h/车道。此外仿真参数如下:采样步长10 s;控制步长为1 min;仿真周期3 h。模型预测控制的预测时域为15 min，控制时域为10 min。

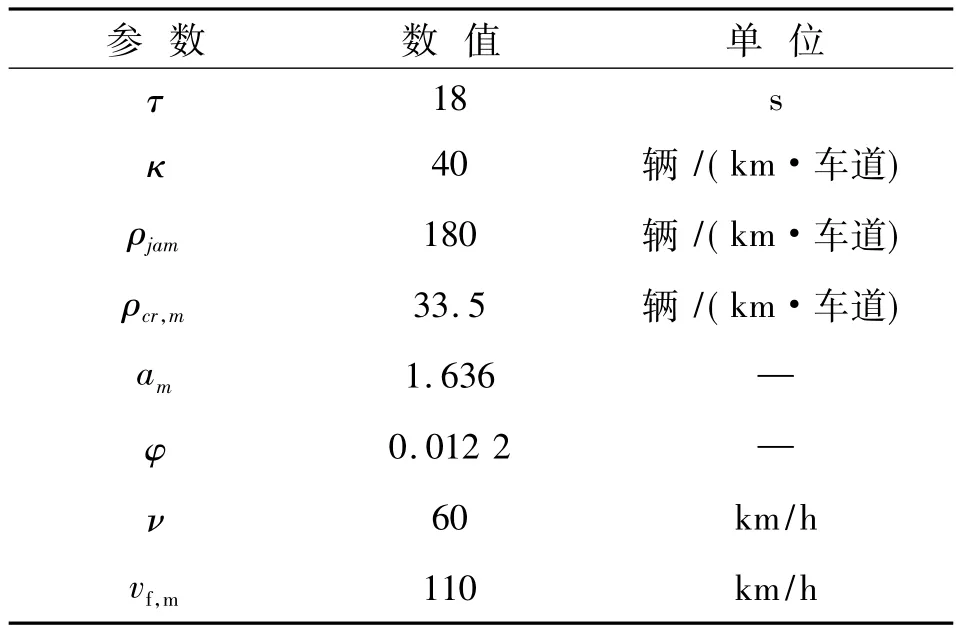
表1 交通流模型参数Tab.1 Parameter values for the traffic flow model

3.2 控制结果分析

针对3.1路网，采用综合性能指标优化得出如图4所示的各匝道调节率时变轨迹。以2号匝道与主路汇合路段为例，图5对比了控制前后该路段的密度和速度变化轨迹。在匝道不控制情况下，随着主线与匝道需求量的增加，入口匝道与快速路主线汇合区车流密度增大，导致车速降低，进而产生拥堵，并向路网上游蔓延，降低整条快速路的通行效率。采取控制措施后，路网的性能得到明显改善。

控制前后路网各评价指标的对比见表2。TTS从无控制时的3 210辆·h降为2 409辆·h，改善了24.96%;在提升路网效率的同时，控制策略使得CO，HC的排放分别降低46.69% 和9.75%，燃油消耗减少20.29%，同时NOx的排放略有增加。

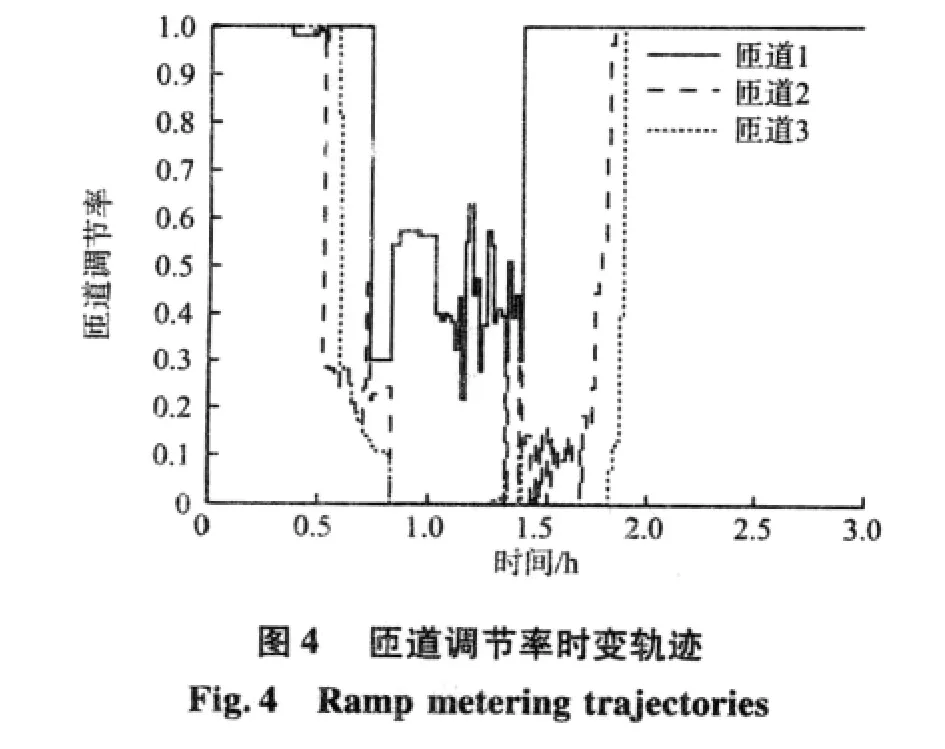
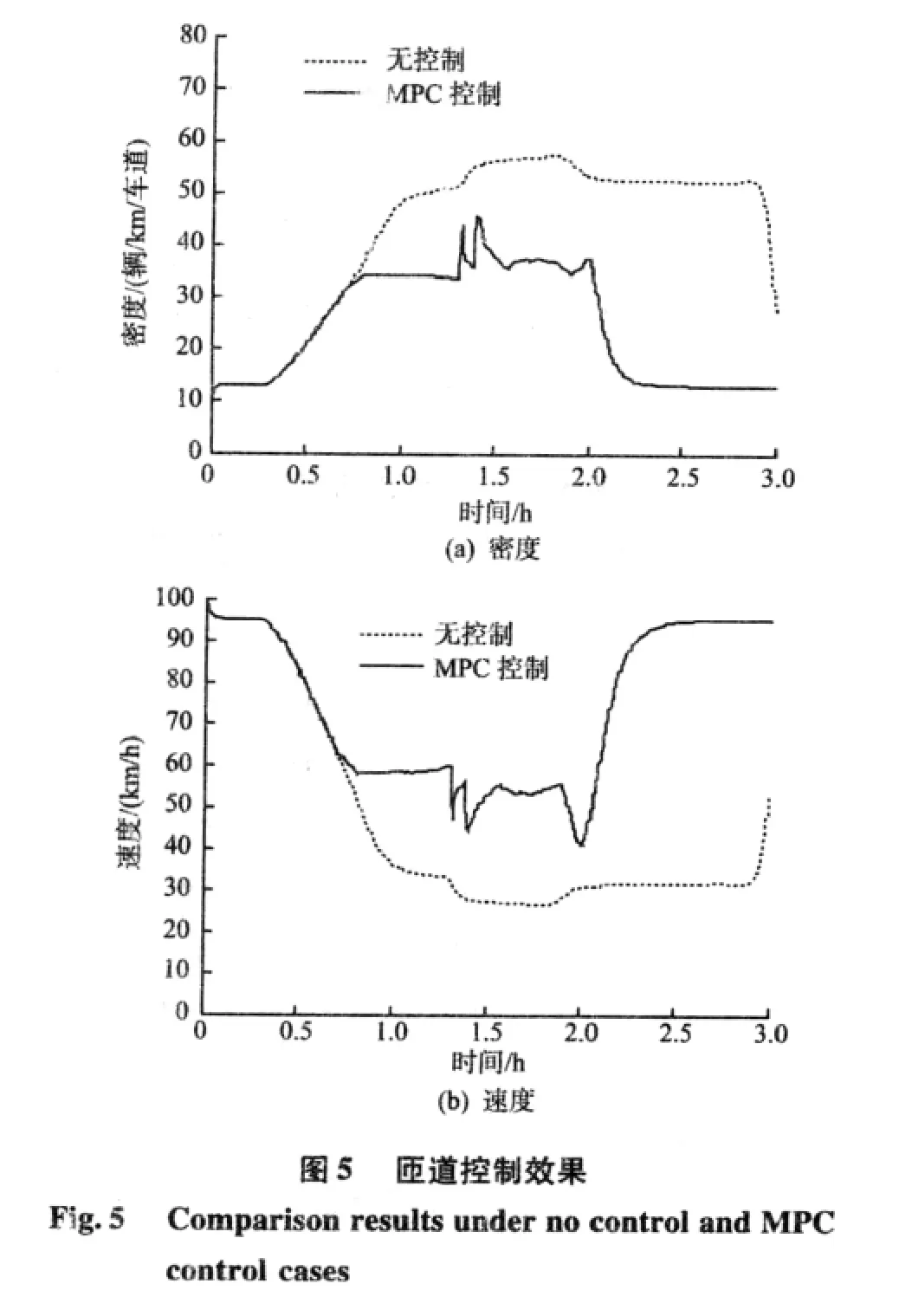
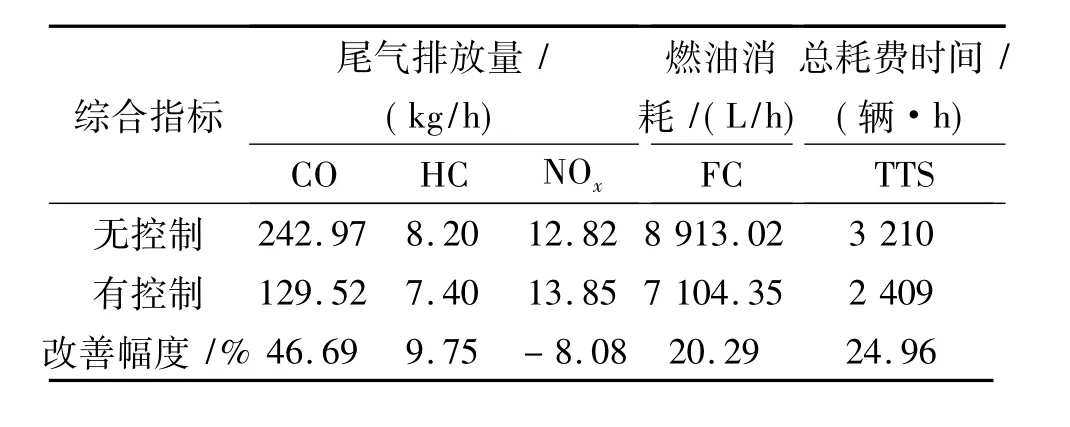
表2 各性能指标仿真结果Tab.2 Simulation results of each objective benefit

图6为在单个采样周期中，匝道控制优化后各个指标相对于不控制情况下的改善百分比。

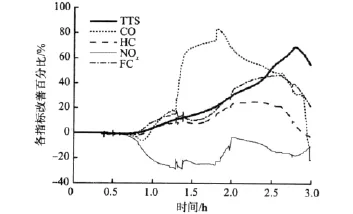
图6 采样周期内各性能指标改善百分比Fig.6 Improvementpercentagesofeach objective benefit during every sampling period

由图6可以看出，匝道优化前后不仅仅通行效率指标与环境指标的演变轨迹不同，而且环境指标中的各尾气排放改善情况也存在较大差异。这是由各尾气排放与机动车运行状态的机理关系所决定的。在仿真的第1至2时，高峰状态导致路网速度大大下降，采取控制策略后，路网速度有所提高，但在该时段只维持在60 km/h附近(见图5)，因此可认为整个时段路网处于低速状态。图6中，CO排放量在此段时间明显减少，改善幅度一度达到80%，而NOx排放量在此段时间相对于不控制情况增长了20%左右，表明仿真结果与理论相吻合。

4 结语

缓解交通拥堵和改善交通污染是目前研究的热门话题。文中设计匝道控制策略时，不仅仅考虑交通效率指标，还引入环境指标因素。以快速路宏观动态交通流模型和微观尾气排放和燃油消耗的集成模型求得机动车尾气排放量和燃油消耗量。基于模型预测控制框架，将入口匝道调节率作为控制变量，给出了入口匝道优化控制命题和基于极小值原理的数值解法，并仿真验证了入口匝道控制能够缓解交通拥挤、改善尾气污染的效果。

此外，文中研究表明改善路网交通拥堵的策略并不一定使所有的污染物排放均减少。如何对环境效益指标和交通效率指标进行合理地权重化是今后研究的重点。希望文中研究能为绿色交通、节能减排以及环境可持续发展提供新的发展思路与技术参考。

［1］Papageorgiou M，Kotsialos A.Freeway ramp metering:an overview［J］.IEEE Trans Intell Transp Syst，2002，3(4):271-281.

［2］Kotsialos A，Papageorgiou M.Nonlinear optimal control applied to coordinated ramp metering［J］.IEEE Trans Control Syst Technol，2004，12(6):920-933.

［3］徐中，陈大伟.基于双层规划模型的城市快速路匝道优化设置研究［J］.交通运输工程与信息学报，2011(1):84-91.

XU Zhong，CHEN Da-wei.Analysis of ramp design and optimization of urban expressway based on bi-level programming model［J］.Journal of Transportation Engineering and Information，2011(1):84-91.(in Chinese)

［4］陈学文，王殿海，金盛，等.城市快速路人口匝道控制方法［J］.吉林大学学报:工学版，2008(S1):43-48.

CHEN Xue-wen，WANG Dian-hai，JIN Sheng，et al.On-ramp metering control strategy of urban expressway［J］.Journal of Jilin University:Engineering and Technology Edition，2008(S1):43-48.(in Chinese)

［5］Bellemans T，De Schutter B，De Moor B.Model predictive control for ramp metering of motorway traffic:a case study［J］.Control Engineering Practice，2006，14(7):757-767.

［6］杨珍珍，干宏程，孙樑.快速路网交通管理策略的环境效益仿真评价方法［J］.计算机应用研究，2011，28(8):2961-2963.

YANG Zhen-zhen，GAN Hong-cheng，SUN Liang.Environment benefits evaluation approach for freeway network traffic management strategies［J］.Application Research of Computers，2011，28(8):2961-2963.(in Chinese)

［7］Zegeye S K，De Schutter B，Hellendoorn J，et al.Integrated macroscopic traffic flow and emission model based on METANET and VT-micro［C］//Proceedings of the International Conference on Models and Technologies for Intelligent Transportation Systems.Rome，Italy:Delft University of Technology，2010:86-89.

［8］Zegeye S K，De Schutter B，Hellendoorn J，et al.Integrated macroscopic traffic flow，emission，and fuel consumption model for control purposes［J］.Transp Res Part C:Emerging Technol，2013，31:158-171.

［9］沙学锋.城市道路机动车动态排放预测模型研究［D］.长春:吉林大学，2011.

［10］胡寿松，王执铨，胡维礼.最优控制理论与系统［M］.北京:科学出版社，2005.