基于合成核支持向量机的风力发电机故障诊断

焦 斌， 郝云锁，2

(1.上海电机学院 电气学院，上海200240;2.华东理工大学信息科学与工程学院，上海200237)

支持向量机(Support Vector Machines，SVM)是Vapnik提出的一种新型的统计学习方法，它是统计学习理论中最年轻的部分，能较好地解决小样本、非线性等实际问题，已成为智能技术领域研究的热点。实践表明，SVM的性能与核函数的类型、核函数的参数以及惩罚系数C有很大关系。因此，研究SVM的核函数选取及参数优化方法，对支持向量机的发展有着重要的意义［1］。PSO算法是近几年发展起来的新型智能优化算法，具有较强的收敛能力和鲁棒性，已应用于机器学习、电力系统、机械设计与通信工程等邻域。

近几年来，国内的许多学者对故障诊断进行深入研究，并取得了一定的成果［2］。郭磊等在滚动轴承的故障诊断中采用小波支持向量机，得到了较高的分类正确率;于德介等利用EMD和SVM方法完成齿轮箱的故障诊断。吴震宇等在内燃机的故障诊断中利用蚁群支持向量机，取得了较好的效果。文中针对SVM核函数的选取及参数的优化，选择以单一的核函数进行合成，得到合成核函数;并采用粒子群智能优化算法，优化SVM的参数;将优化后的合成核SVM在UCI数据集上进行仿真实验，利用优化的SVM建立多分类决策模型，对风力发电机进行故障诊断。

1 支持向量机

1.1 支持向量机原理

支持向量机是结构风险最小化方法的近似实现，从线性可分模式的情况来看，它的主要思想就是建立一个超平面作为决策面，该决策面不但能够将所有训练样本正确分类，而且使训练样本中离分类面最近的点到分类面的距离最大［3］。

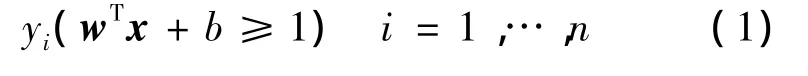
的约束条件下求

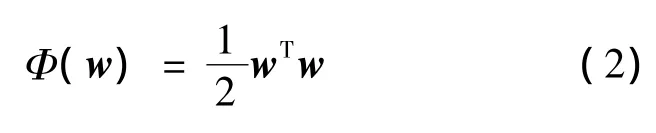
的最小值。

这个约束优化问题称为原问题，该问题可以利用Lagrange乘子方法将其转化为对偶问题解决，即

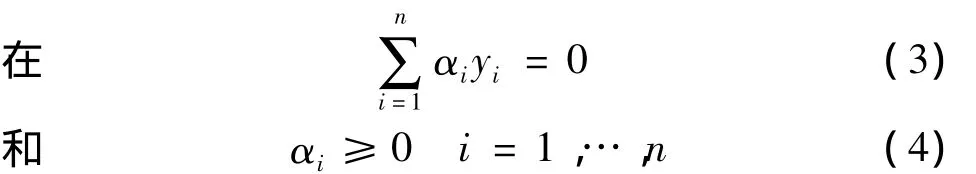
的约束条件下，求

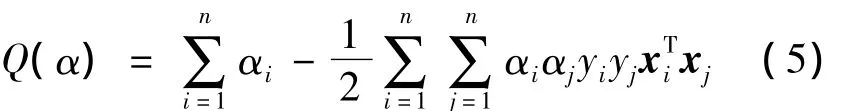
的最大值。

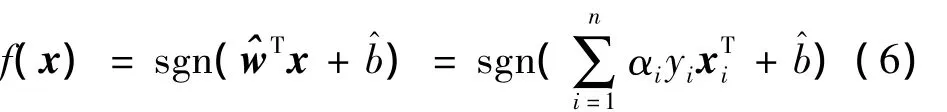
对于非线性不可分模式，可通过某种特定的非线性映射，将样本空间映射到高维特征空间。其线性可分，并在高维特征空间中构造出最优分类超平面，从而实现分类，这种非线性映射函数也称为核函数［4］。假设φ(x)表示输入向量x在特征空间所映射的“像”，则核函数可表示为

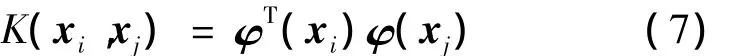
根据泛函的有关理论，只要核函数K(xi，xj)满足Mercer条件，它就对应某一变换空间的内积。因此，用适当的内积核函数就可以实现从低维空间向高维空间的映射，从而实现某一非线性变换后的线性分类，而计算复杂度却没有增加。与线性可分模式相比，此时的约束条件式(4)变为

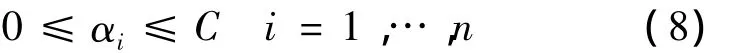
其中，C用以控制对错分样本的惩罚程度。

最优分类函数变为

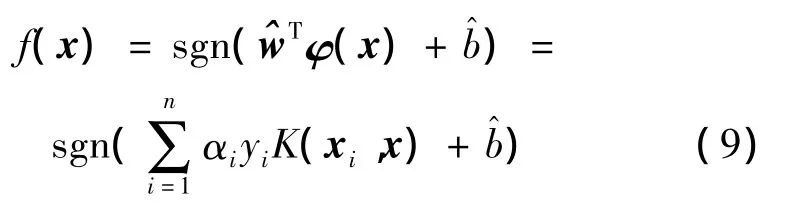
选择不同的内积核函数可形成不同的算法，目前在分类方面研究较多也较常用的核函数有4种，即线性核函数、多项式核函数、径向基核函数和Sigmoid核函数。

1.2 合成核函数

多核模型是一类灵活性更强的基于核的学习模型，近来的理论和应用已证明利用多核代替单核能够增强决策函数的可解释性，并可获得比单核模型或单核机器组合模型更优的性能构造多核模型［5］。

核函数主要分为全局核函数和局部核函数两大类。全局核函数具有全局特性，允许相距很远的数据点都可以对核函数的值有影响，泛化性能强、学习能力较弱;而局部核函数具有局部性，只允许相距很近的数据点对核函数的值有影响，学习能力强，泛化性能较弱［6］。

径向基核函数

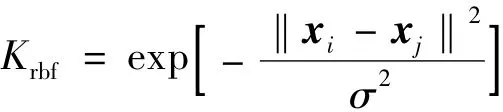
为典型的局部核函数，图1为当p分别取10，5，3.5，2.5，2时高斯核函数曲线(其中图例中的 p即为1/σ2)。

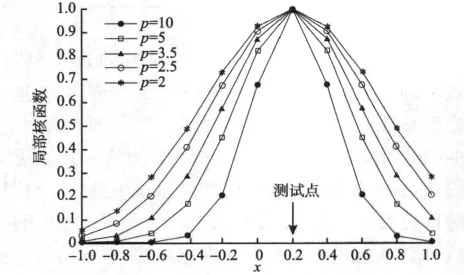
图1 径向基核函数曲线(局部核)Fig.1 Mapping characteristics of RBF(local kernel)

由图1可以看出，当输入数据点在测试点附近时，核函数的值就有明显变化，这也说明了高斯核函数是一种局部性核函数。

多项式核函数Kpoly=(+1)d为典型的全局核函数，图2 为当d分别取1，2，4，5，6 时多项式核函数的曲线。

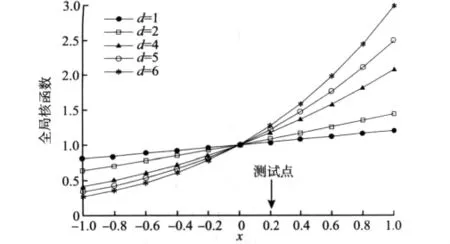
图2 多项式核函数曲线(全局核)Fig.2 Mapping characteristics ofPolynomial(global kernel)

由图2可以看出，当输入数据点远离测试点0.2时，核函数的值才有明显改变，由此说明了多项式核函数属于全局性核函数。

由于多项式核函数和高斯核函数分别是全局核和局部核的典型代表，且都有各自的局限性。把这两类核函数混合起来，组成混合核函数，由该混合核函数构成的支持向量机同时具备两个单核的优点，具有更好的学习能力和泛化性能［7］。文中采用径向基核函数和多项式核函数的合成核函数训练支持向量机。径向基核函数和多项式核函数的合成核可定义为

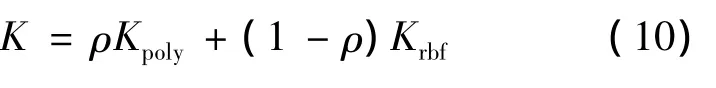
其中，p为合成核函数的协同因子，取值范围为0≤p≤1。为了说明合成核函数比单核函数具有更好的泛化学习能力，取径向基核函数1/σ2=5，多项式核函数 d=1，协同因子ρ的取值范围为0.5～0.95，测试点仍取0.2，得到合成核函数的曲线如图3所示。

图3 合成核函数曲线Fig.3 Mapping characteristics of composite kernels

由图3中可以看出，合成核函数同时具有局部核和全局核的效果，图例中并没有展示出ρ较小时候的曲线，因为此时全局核的影响效果非常的小。当ρ增大时，多项式核函数的全局效果更加明显。

2 基于PSO的SVM参数调整算法

粒子群优化算法(PSO)是Eberhart等［8］提出的一种进化计算技术。PSO求解优化问题时，问题的解对应于搜索空间中一只鸟的位置，这些鸟为“粒子”(Partical)。每个粒子都有自己的位置和速度(决定飞行的方向和距离)，还有一个由被优化函数决定的适应值。各个粒子记忆、追随当前的最优粒子，在解空间中搜索［9］。

PSO初始化为一群随机粒子(随机解)，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pbest;另一个是整个种群目前找到的最优解，这个极值是全局极值gbest。在找到这两个最优值时，粒子根据如下公式更新自己的速度和位置［10］:

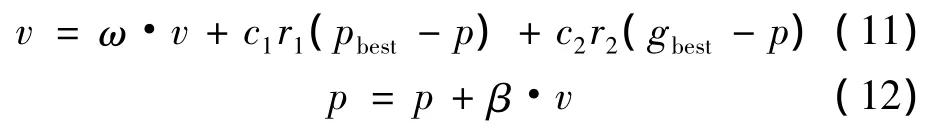
其中:p为粒子当前的位置，表示SVM参数{C，σ}的当前值;υ∈［－vmax，vmax］为粒子的速度，决定下一代{C，σ}的更新方向和大小;β为为约束因子，控制速度的权重，通常取1;c1，c2为学习因子，通常取c1=c2=2;r1，r2为介于(0，1)之间的随机数;ω为非负数，称为惯性因子。

PSO是近几年兴起的一种进化算法，将粒子群算法和支持向量机相结合建立风力发电机故障诊断的模型是有效可行的。粒子群优化算法实现简单、优化效率高，通过信息的共享及传递大大缩短了寻优时间，提高了收敛速度。文中选用k-fold交叉验证误差作为SVM参数选择的目标值，利用PSO算法对径向基核函数、多项式核函数和合成核函数的核参数及惩罚因子进行优化。在PSO寻优过程中，合成核的权系数是动态调整的，对每一次迭代寻优操作获得一组权系数ρ，利用这组权系数产生核即得到的是一个单核。SVM用这个单核对数据集进行分类，计算分类精度后再迭代调整权系数。

算法具体步骤描述如下:

1)读取样本数据，随机产生一组{C，σ}作为粒子的初始位置。

2)把整个样本平均分成K个互补包含的子集s1，s2，…，sk。

3)根据当前的{C，σ}训练SVM，计算k-fold交叉验证误差;① 初始化i=1;② Si子集作为检验集，其余的子集合并起来作为训练集，训练SVM;③计算第i子集的泛化误差ei=mean(Si－)2，令i=i+1，重复②直到i=k+1;④计算k次泛化误差的平均值得到k-fold交叉验误差。

4)以k-fold交叉验证误差作为适应值，并记录个体与群体所对应的最佳适应值的位置为pbest和gbest，根据式(10)，式(11)搜寻更好的{C，σ}。

5)重复2)直到满足最大迭代次数。

6)结束。

对于PSO算法优化支持向量机参数的实现，相当于把SVM模型的构造、预测算法嵌入到PSO计算适应值的步骤当中，因此模型的回归精度有很大的提高。用PSO优化SVM，只需随机选取少量样本进行模型训练，其余大量样本作为测试用。这点不同于其他故障诊断方法，它们是将大量样本用作训练，少量样本用作测试。所以，理论上PSO更加节省时间，而由此得到的学习模型也具有较好的预测能力。特别是对一些大样本数据，更能体现PSO和SVM的优势。本，各样本有13个属性;Breast Cancer为2分类问题，有683个样本，各样本有10个属性。考虑到算法的随机性。把每个数据集分成4个子集，每次取其中一个作为测试集，其余3个合并为训练集，取4次实验的均值作为该数据集的分类结果。初始化PSO算法的参数，c1=c2=2，ωmax=1.2，ωmin=0.4，分别训练径向基核函数支持向量机，多项式核函数支持向量机，合成核函数支持向量机;对4组数据进行分类，并对分类精度进行比较，具体结果见表1。3种支持向量机经过参数寻优得到的参数见表2。

3 仿真实验

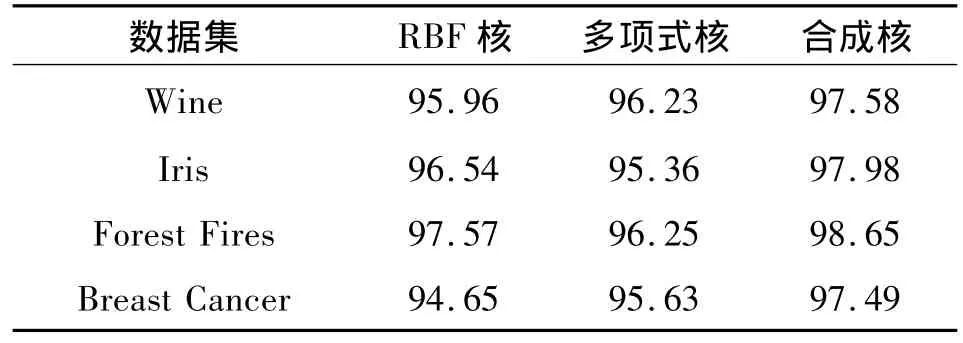
表1 RBF核、多项式核和合成核支持向量机对数据分类正确率的比较Tab.1 Classification of composite kernel compares with RBF and polynomial kernel %

文中实验采用 UCI数据集中的 Wine，Iris，Forest Fires，Breast Cancer 4组数据进行:Wine为3分类问题，有178个样本，各样本有13个属性;Iris数据为3分类问题，有150个样本，各样本有4个特征属性;Forest Fires分为2分类问题，有517个样

由表1中可以看出，对于每一个数据集的数据，合成核函数分类器的正确率都比单个核函数的正确率要高，而且比较稳定。以上结果表明PSO算法在参数寻优中的优越性和良好的搜索能力，采用合成核函数的支持向量机与单核支持向量机相比提高了分类精度。

表2 RBF核、多项式核和合成核支持向量机所对应的参数Tab.2 Parameters of RBF，polynomial and composite kernels

4 实例应用

风力发电机齿轮箱是传动链的一部分，起着功率传送功能，是风机中比较重要的部件。由于叶轮的直径较大，一般的风速条件下，它的转速比较低，不能满足发电机发电的转速要求。通过齿轮箱的增速作用，使速度达到要求，把叶片获得的动能传给发电机进行发电。

齿轮箱是风机中最容易出故障的部位［11］。故利用文中提出的合成核分类器，针对风力发电机齿轮箱的正常、断齿、齿面磨损、轴承内圈损坏及轴承外圈损坏5种典型工况，进行故障模式识别分类。

基于合成核函数支持向量机模型，结合决策树法和投票法，建立多分类SVM决策模型，设计出的基于合成核函数分类器的风机齿轮箱故障诊断多分类模型(见图 4)［12］。

图4 中A代表正常的状况，B，C，D和E分别代表断齿，齿面磨损，轴承内圈损坏和轴承外圈损坏等4种故障类型。故障诊断决策模型中，第1层结构是用来判断风机齿轮箱是否正常工作的，并以A类正常工作的样本集作为正的样本(+1)，其他的故障类型样本集作为负的样本(－1)进行训练。模型的第2层是用以识别风机齿轮箱的4种故障类型的，每个SVM分类器都以第1个故障类型作为正样本输出。在所有诊断的4种故障类型两两之间建立6个SVM分类器，再利用它们相对应的2个样本对每个分类器进行训练，实现对风机齿轮箱的故障诊断。

通过风机实验平台得到的一组特征参量，进行数据分析和归一化处理［13］，10组待诊断的齿轮箱故障样本的振动信号特征参数见表3。

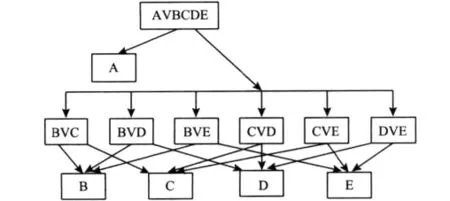
图4 基于多分类SVM的风机齿轮箱故障诊断决策模型Fig.4 MCSVM fault decision model of wind turbine gearbox

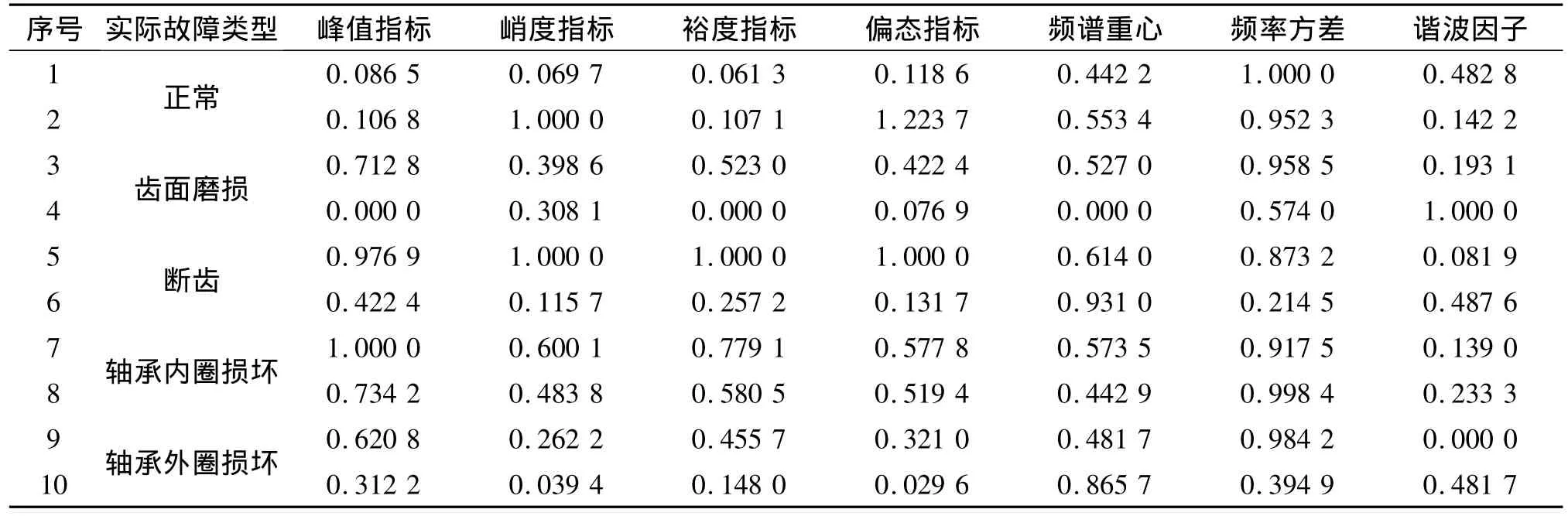
表3 齿轮箱待诊断样本的振动信号特征参量Tab.3 Vibration signal characteristic parameters of staying sample of gearbox

利用多分类SVM决策流程，对表3中的10组数据齿轮箱故障样本进行故障诊断，可以得到每个不同的SVM分类器对其中所提出的故障样本输出结果;根据SVM的原理可以将其分为正负两种类型，样本的输出结果见表4。每个待诊断样本在齿轮箱5种状态模式中的最终得票数情况及最终的诊断结果见表5。根据输出结果的符号判断待诊断样本的归属，并且在相对应的齿轮箱故障类型的得票数上加1。以BC两两分类器为例，假如输出的为正数，那么就在B故障类型的得票数上加1;反之输出为负，在C故障的得票数上加1，根据最后的得票数判断该样本的最终故障类型［14］。从结果中可以看出，合成核函数训练的支持向量机在风力发电机故障诊断中有着良好的稳定性和分类精度。

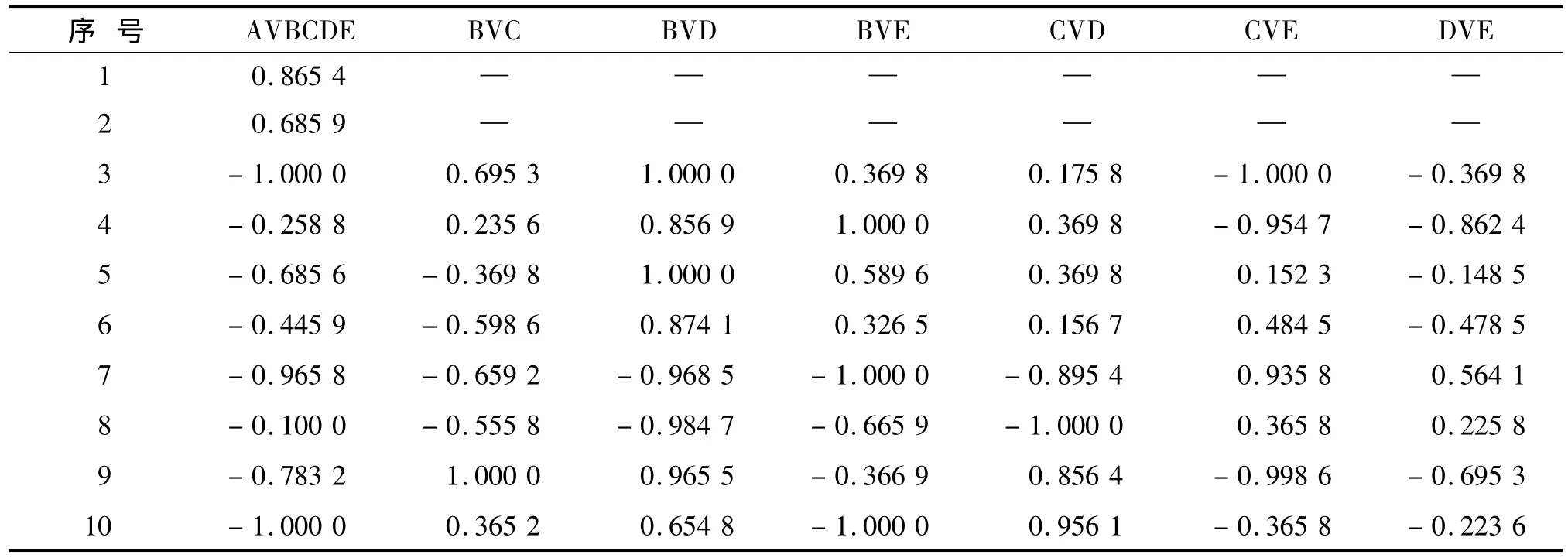
表4 每个SVM分类器对样本的输出结果Tab.4 Output of sample about each SVM classifier

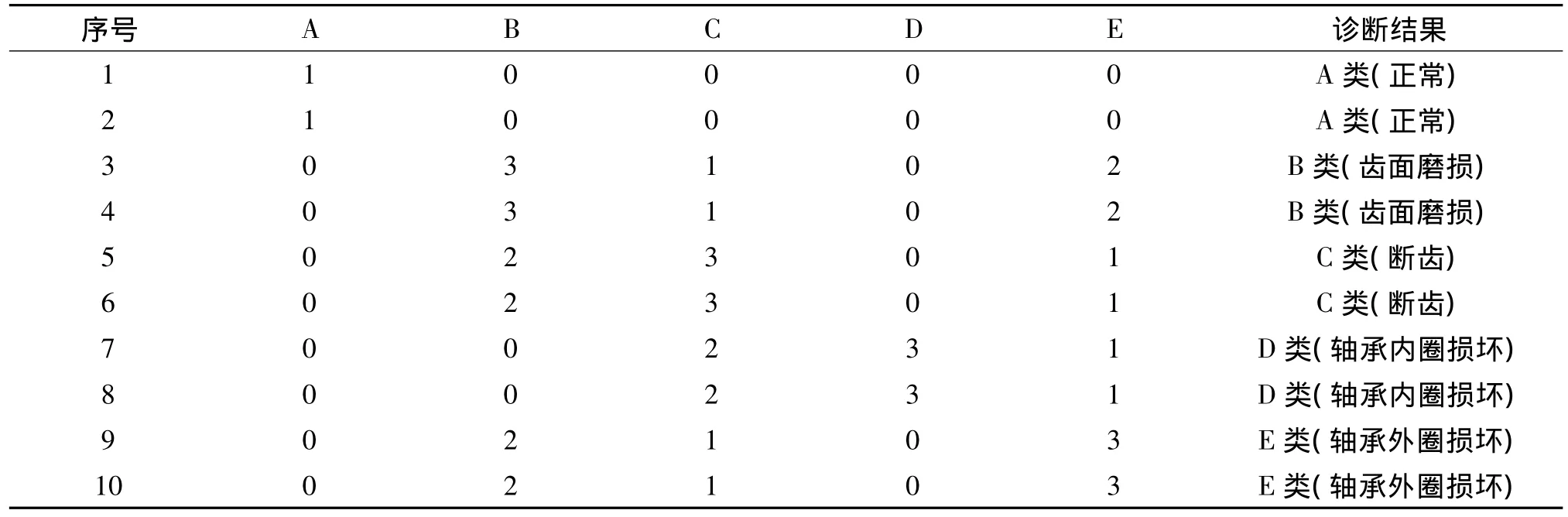
表5 SVM模型中的投票结果和诊断结果Tab.5 Result of the vote and diagnosis in SVM

5 结语

文中利用合成核支持向量机进行分类，弥补了单核在学习能力和泛化能力上的不足，并利用粒子群智能优化算法对支持向量机进行参数寻优。通过理论分析和仿真实验，表明利用合成核函数支持向量机进行分类，不仅提高了分类的准确率，而且分类器的稳定性也得到了很大的提高。把合成核的支持向量机应用到风力发电机的故障诊断中，建立决策模型取得了良好的效果。

［1］Vapnik V N.The Nature of Statistical Learning Theory［M］.New York:New York Springer Verlag，1995.

［2］李红卫，杨东升，孙一兰，等.智能故障诊断技术研究综述与展望［J］.计算机工程与设计，2013，34(2):632-637.LI Hong-wei，YANG Dong-sheng，SUN Yi-lan，et al.Study review and prospect of intelligent fault diagnosis technique［J］.Computer Engineering and Design，2013，34(2):632-637.(in Chinese)

［3］SmolaA J，Scholkopf B A.Tutorial on support vector machine［R］.NeuroCOLT2 Technical Report NC2-TR-1998-030.London:Royal Holloway College，University of London，1998.

［4］Cristianini N，Shawe-Taylor J.An Introduction to Support Vector Machine and other Kernel-Based Learning Methods［M］.Cambridge:Cambridge University Press，2004.

［5］汪洪桥，蔡艳宁.多核学习方法［J］.自动化学报，2010，36(8):1038-1041.WANG Hong-qiao，CAI Yan-ning.On multiple kernel learning methods［J］.Acta Automatica Sinica，2010，36(8):1038-1041.(in Chinese)

［6］刘明，周水生，吴慧.一种新的混合函数支持向量机［J］.计算机应用，2009，29:167-168.LIU Ming，ZHOU Shui-sheng，WU Hui.SVM based on new mixed kernel function［J］.Journal of Computer Applications，2009，29:167-168.(in Chinese)

［7］Smits G F，Jordaan E M.Improved SVM regression using mixtures of kernels［C］//Proceedings of the International Joint Conference on Neural Networks.Honolulu:IEEE，2002，3:2785-2790.

［8］Kennedy J，Eberbart R C.Particle swarm optimization［C］//Proc IEEE IntConf on Neural Networks.Piscataway:IEEE Service Center，1995:1942-1948.

［9］SHI Yu-hui，Eberhart R C.A modified particle swarm optimizer［C］//Proceedings of 1998 IEEE International Conference on Evolutionary Computation.Anchorage，AK:IEEE，1998:1945-1950.

［10］Eberhart R，Kenney J.A new optimizer using particle swarm theory［C］//Proc of the Sixth International Symposium on Micro Machine and Human Science.Piscataway，NJ:IEEE Press，1995:39-43.

［11］吴今培.智能故障诊断技术的发展和展望［J］.振动、测试与诊断，1999，19(2):79-86.WU Jin-pei.Development and forward of intelligent trouble diagnosis［J］.Journal of Vibration，Measurement and Diagnosis，1999，19(2):79-86.(in Chinese)

［12］Moreira M，Mayoraz E.Improved Pairwise Coupling Classification with Correcting Classifiers［M］.Machine Learning:ECMI-98.Berlin，Heidelberg:Springer Berlin Heidelberg，1998:160-171.

［13］Patton R J.Robustness in model based fault diagnosis:1995 situation［J］.Annual Review in Control，2007，43(1):357-365.

［14］霍雨佳.支持向量机分类算法的研究与应用［D］.河北:华北电力大学，2007.