基于支持向量机的矿浆管道堵塞信号识别方法

马 帅， 王晓东*，2， 吴建德，2， 范玉刚，2， 黄国勇，2

(1.昆明理工大学信息工程与自动化学院，云南昆明650500;2.云南省矿物管道输送工程技术研究中心，云南昆明650500)

近年来，长距离输矿管道在我国得到了快速的发展，作为五大运输方式之一的管道输送相比较于铁路、公路具有不占或少占土地、不污染环境，投资费用低、自动化程度高等一系列明显的优点，成为冶金矿山企业建设设计铁精矿外运的主要方式之一。由于矿物管道设计一般多在地形复杂的高山、高原地区，给管道的正常输送带来不利的影响;特别是在管道的转弯和有较大落差的连接处容易造成矿浆管内浆体的流速不稳定，导致管道堵塞，严重影响了冶金矿山企业的正常生产，造成巨大的经济损失。目前，常用的管道检测装置主要通过管道的输送压力、流量等参数的变化来判断［1］。此类方法受输送物质特性及输送工况等诸多因素影响，且报警发生在泄漏之后［2］。因此，针对目前管道检测出现的问题，特别是矿浆管道堵塞检测难问题，基于模式识别的方法能够较好地识别出压力信号的异常，并及时识别故障信号。

目前，基于传统统计学理论的神经网络的模式识别方法在实际工程中应用较多，但是，其结构参数往往依赖于多次的实验才能确定，而且需要大量的故障样本对其进行训练。而在实际的工业生产中，大量存在的是正常操作条件下的数据，只有少量故障数据。神经网络分析可以做到经验风险最小化，但与实际风险仍有较大差异，泛化性差，其诊断的准确性一直不能达到工程的要求［3］。支持向量机(Support Vector Machine，SVM)是在统计学习理论基础上发展起来的一种新的通用机器学习方法。SVM较好地解决了以往许多学习方法中小样本、非线性和高维数等实际难题，可以使在小样本情况下建立的分类器具有很强的推广能力［4］。

针对矿浆管道堵塞检测的特殊性，管道堵塞技术面临的一个难题就是管道堵塞样本数据不易获取，此外也很难对获取的非平稳随机信号进行特征提取，这些问题严重地制约着管道堵塞检测技术的发展。鉴于支持向量机与其他机器学习方法的本质区别在于它是针对小样本、非线性问题提出的，它能在训练样本很小且非线性的情况下达到很好的分类推广效果，而且它不需要预先知道故障分类的先验知识［5］。因此，支持向量机可以被应用于管道堵塞技术的检测领域。

有效识别在矿浆管道完全堵塞前将小堵塞即不完全堵塞的压力信号、流量信号识别出来显得至关重要。文中对传统统计学与统计学习理论进行比较，分析了传统学习方法的局限性，然后将基于支持向量机分类方法用于管道堵塞信号的识别，并将实验结论与神经网络方法对比，证明该方法是可行的，有效的。

1 基于传统统计学理论的局限性

传统统计学理论与统计学习理论相比，局限性主要表现在以下两方面［6］。

1.1 对学习样本的要求高

传统统计学理论对样本的要求比较高，如神经网络方法，包括两个方面:样本的数量和样本的质量。在管道堵塞检测中，要求样本数据的分布能覆盖所有管道堵塞模式，这决定了样本的数量会很多，并且类似的工况样本不能有矛盾或冲突。然而，在实际的工业生产中只有少量的故障样本，大量存在的是正常工况下的数据，并且管道堵塞的故障模式是有限的。因此神经网络等方法不能满足检测堵塞信号的样本数目，及其有限的管道堵塞应用。

1.2 模型的泛化能力差

传统学习方法中采用的经验风险最小化(ERM)准则常常定义为

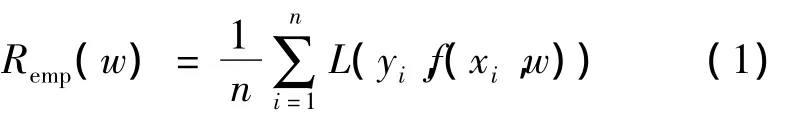
其中，Remp(w)是利用已知的经验数据(训练样本)来计算，因此被称为经验风险。利用对参数w求经验风险来逐渐逼近理想的期望风险的最小值。而神经网络故障诊断模型基于经验风险最小化的原则，这样很容易导致神经网络的过学习，即训练误差过小而导致泛化能力下降。根据统计学习理论，对指示函数集中的所有函数(包括使经验风险最小的函数)、经验风险Remp(w)和实际风险R(w)之间以至少1－η的概率满足以下关系［7］:

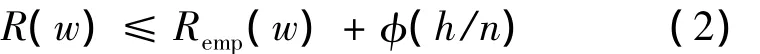
式中:R(w)为实际风险;Remp(w)为经验风险;h为函数集的VC维;n为样本数。

在训练样本数目有限的条件下，模型的VC维越高则置信范围越大，真实风险与经验风险之间可能的差别就越大。这就是出现过学习的原因，从而导致识别模型的泛化性能差。而机构风险最小化原则(SNM)将预测函数集构造为函数子集序列，使各个子集按照VC维的大小排列，在各个子集间折中考虑经验风险Remp(w)和置信范围φ(h/n)，取实际风险最小［8］。

基于以上分析，针对传统的统计学理论局限性，支持向量机方法建立在统计学习理论的结构风险最小原理和采用结构风险最小原理及VC维的基础上，根据有限样本信息在模型中的复杂性和学习能力之间寻求最佳折中，能够兼顾训练误差和泛化能力，从而获得更高的推广能力。

2 支持向量机基本原理

支持向量机是在统计学习理论基础上发展起来的一种新的学习方法，具有很多优于已有方法的性能［9］。支持向量机作为一种小样本学习理论，建立在结构风险最小化的基础上，对有限的训练样本集，能够获得最优的推广能力，较好地解决了过学习和欠学习以及局部极小点等问题，已被成功地应用于人脸识别、语言识别等领域［10］。支持向量机的核心思想是把输入空间的样本通过非线性变换映射到高维核空间，在高维核空间求取具较低VC维的最优分类超平面。分类方法如下:

设有一个训练样本集:{(x1，y1)，(x2，y2)，…，(xn，yn)}，其中 xn∈ Rn，yn∈ R，xn为支持向量机的输入数据，yn为对应的输出数据。要实现最优超平面需要对训练样本数据进行正确分类，则要满足

根据结构风险最小化原则，将最优分类面问题表示成求解二次凸优化问题:

其中:w为超平面系数向量;b为偏置;ξi为松弛变量;C为惩罚参数。

将约束化问题转化为构造Lagrange函数求解，利用对偶原理可得到上述优化问题的对偶描述:

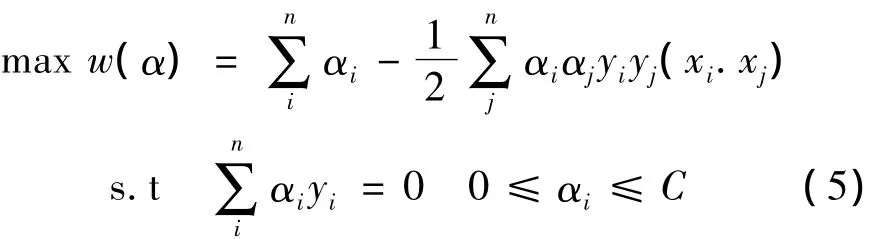
其中，αi为朗格朗日乘子。若为最优解，则

即最优分类面的权系数向量w*是训练样本量yi和xi的线性组合。相应的最优分类判别函数:

对于线性不可分问题，可以在其分类方程中引入一个松弛变量ξi≥0来解决。

而当训练样本集非线性问题时，通常可以将输入样本映射到某个高维特征空间，进而在该空间中构造最优分类面并在这一空间中求最优分类面。此时对应的最优分类判别函数为

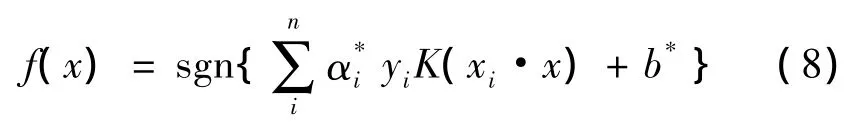
上式即为支持向量机。

支持向量机的分类函数形式上类似于一个神经网络，输出量是输入向量与中间核函(Kernel function)节点乘积的线性组合。支持向量机在训练中包括选择合适的核函数，它的训练能力跟所选择的核函数以及所选择的相关参数有很大的关系，尤其是核参数以及模型参数中的惩罚参数C有很大的关系。分类计算中可以选择不同的核函数，通常有多项式核函数、径向基核函数、高斯核函数以及线性核函数。文中支持向量机采用径向基核函数(RBF)。

3 管道堵塞辨识实例分析

3.1 实验算法步骤

实验数据采用M宽(M表示某一泵站压力、流量的采样值)的数据样本作为支持向量机的输入值，每组输入为泵站进口压力值和流量值组成。本实例中M=130，使用其中100组作为训练样本，对另外30组进行预测分类，样本采样间隔为2 min。

1)随机从M宽的数据样本抽取训练样本。

2)选择合适的核函数，文中选用RBF核函数。

3)支持向量机的训练方法很多，网格搜索法是将C和γ分别取M个值和N个值，对M×N个(C，γ)的组合，分别训练不同的支持向量机，再估计其学习精度，从而在M×N个(C，γ)的组合中得到学习精度最高的一个组合作为最优参数［11］。基于支持向量机矿浆管道堵塞信号识别方法就是采用该思想。

4)训练模型的参数寻优(惩罚因子C和参数 γ)。

5)向训练好的样本模型中输入测试样本，检测分类效果。

3.2 识别效果与分析

由于输矿管道的特殊性，在管道完全堵塞的前期会形成一些小的堵塞即不完全堵塞，对这些不完全堵塞的压力信号以及流量信号用支持向量机进行辨识，对于管道堵塞起到一个很好的预警作用。文中采用云南某公司2010年某一泵站输矿管道压力、流量数据进行检测，在识别模型问题上将SVM，RBF人工神经网络测试结果进行性能比较分析，评估SVM的分类辨识效果。

为了消除样本在数值上相差较大的影响，提高模型的学习速度和预测精度，对输入样本进行归一化处理。归一化公式为

利用Libsvm工具箱中自带的网格参数寻优方法(Cross search method)，自动寻找RBF核中的C参数、Gammam参数，获得最佳参数值C=0.062 5，g=5.78，交叉检验准确率(Cross validation accuracy)为99%。SVC参数选择结果如图2所示。

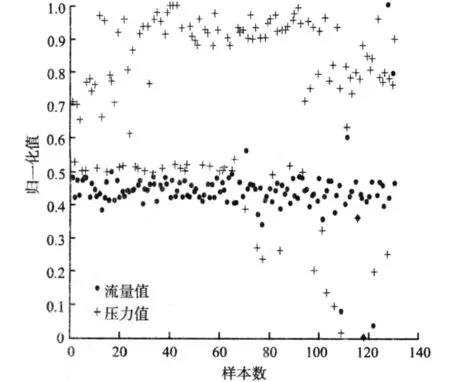
图1 样本归一化数据Fig.1 Figure of sample data for normalization

采用100组样本数据作为训练集，建立堵塞识别模型，对30组数据进行分类预测，准确率达93.33%。效果如图3所示。

利用同样的训练集和测试集，RBF人工神经网络分类预测效果如图4所示。

从图3和图4的测试结果可以看出，相比较于RBF人工神经网络，支持向量机在小样本中显示出

4 结语

图2 SVC参数选择结果Fig.2 Figure of SVC Parameter selection result

图3 测试集SVM预测结果Fig.3 FigureoftestsetsSVM neuralnetwork prediction result

针对矿浆管道沿线堵塞事件检测这一典型的分类问题，较好地将支持向量机用于管道堵塞信号的识别。测试结果表明，基于支持向量机的管道识别方法比人工神经网络方法学习训练速度快，分类良好的处理能力，避免了RBF人工神经网络过学习现象，这是因为神经网络等传统的学习方法是基于经验风险最小化原则，但是经验风险最小不能确保实际风险最小，因此出现了过学习的现象。而基于结构风险最小化原则的支持向量机比RBF人工神经网络显示出更好的分类能力，识别效果优于RBF人工神经网络。处理效果性能好。基于结构风险最小化原则的支持向量机比基于经验风险最小化原则的RBF人工神经网络学习方法有更好的泛化能力和更高的分类准确率，因此更适合小样本条件下的机器学习。该方法可以有效地用于识别矿浆管道堵塞事件，提高管道堵塞检测的准确率，从而达到安全生产的目的。因此基于支持向量机的矿浆管道堵塞信号识别方法可推广到油气管道堵塞信号的检测中，应用前景广阔。但是，目前基于支持向量机的管道堵塞信号识别方法仍需在其核函数和参数选择中进一步改进。

图4 测试集RBF神经网络预测结果Fig.4 Figure of test sets RBF neural network prediction result

在下一步工作中，将对支持向量机识别堵塞信号方法进行改进，通过实验进一步完善识别效果。

［1］杨杰，王桂增.输气管道泄漏诊断技术综述［J］.化工自动化及仪表，2004，31(3):1-5.YANG Jie，WANG Gui-zeng.Leak detection and location methods for gas transport pipelines［J］.Control and Instruments in Chemical Industry，2004，31(3):1-5.(in Chinese)

［2］曲志刚，封皓，靳世久，等.基于支持向量机的油气管道安全监测信号的识别方法［J］.天津大学学报:自然科学版，2009，42(5):465-470.QU Zhi-gang，FENG Hao，JIN Shi-jiu，et al.An SVM-based recogntion method for safety monitoring signals of oil and gas pipeline［J］.Journal of Tianjin University:Natural Science Edition，2009，42(5):465-470.(in Chinese)

［3］康维新，彭喜元.基于二层SVM多分类器的桩基缺陷诊断［J］.电子学报，2008，12(12A):66-70.KANG Wei-xin，PENG Xi-yuan.The defects diagnose of pile foundation based on two-layermultiple-classifier of SVM［J］.Acta Electronica Sinica，2008，12(12A):66-70.(in Chinese)

［4］姜万录，吴胜强.基于SVM和证据理论的多数据融合故障诊断方法［J］.仪器仪表学报，2010，31(8):1738-1743.JIANG Wan-lu，WU Sheng-qiang.Multi-data fusion fault diagnosis method based on SVM and evidence theory［J］.Chinese Journal of Scientific Instrument，2010，31(8):1738-1743.(in Chinese)

［5］赵艳燕.基于支持向量机的管道泄漏声发射研究［D］.北京:北京化工大学，2010.

［6］梅建新，段汕，潘继斌.支持向量机在小样本识别中的应用［J］.武汉大学学报:自然科学版，2002，48(6):732-736.MEI Jian-xin，DUAN Can，PAN Ji-bin.The application of support vector machines in recognition of small sample［J］.Journal of Wuhan University:Natural Science Edition，2002，48(6):732-736.(in Chinese)

［7］Burges C J C.Atutorial on support vector machines for pattern recognition［J］.Data Mining and Knowledge Discovery，1998，2(2):121-167.

［8］范晓静，张来斌，梁伟，等.基于支持向量机的管道泄漏检测方法研究［J］.仪器仪表学报，2008，28(4):236-239.FAN Xiao-jing，ZHANG Lai-bin，LIANG Wei，et al.Research of leakage detection for pipelines based on support vector machine［J］.Chinese Journal of Scientific Instrument，2008，28(4):236-239.(in Chinese)

［9］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26(1):32-42.ZHANG Xue-gong.Introduction to statistical learning theory and support vector machines［J］.Acta Automatica Sinica，2000，26(1):32-42.(in Chinese)

［10］边肇祺，张学工.模式识别［M］.北京:清华大学出版社，2000.

［11］李琳，张晓龙.基于RBF核的SVM学习算法的优化计算［J］.计算机工程与应用，2006(29):190-204.LI Lin，ZHANG Xiao-long.Optimization of SVM with RBF kernel［J］.Computer Engineering and Applications，2006(29):190-204.(in Chinese)